 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Темы контрольной работы
|
|
Для специальностей 15.02.01, 21.02.03, 21.02.02, 18.02.09, 15.02.07
1. Элементы теории множеств (№ 1-10)
2. Решение линейных систем уравнений методом Крамера и Гаусса (№ 11-20)
3. Элементы комбинаторики (№ 21-30)
4. Дифференциальное исчисление (№ 31-40)
5. Интегральное исчисление (№ 41-50)
6. Дифференциальные уравнения (№ 51-60)
7. Элементы теории графов (№ 61-70)
Темы контрольной работы
Для специальностей 15.02.01, 21.02.03, 21.02.02, 18.02.09, 15.02.07
Тема 1. Элементы теории множеств
№ 01-10. Для данных множеств M и N найти: M U N; M ∩ N; N/М;M/N;
M x N; M + N.
Совокупность всех подмножеств множества M:
01. M={5;6;8}; N={2;3;4;5};
02. M={p;3;e}; N={1;2;p;e};
03. M={12;13;15}; N={11;12;13;15}
04. M={a;b;c}; N={b;c;d;e}
05. M={2;3;5} N={5;6;8;9}
06. M={2;3;4} N={1;4;5;6}
07. M={1;2;3} N={3;4;5;6}
08. M={3;4;5} N={4;5;6;7}
09. M={2;3;e} N={3;e;2;2;}
10. M={6;7;9} N={3;4;5;6}
Тема 2. Решение линейных систем уравнений методами
А) Крамера, б) Гаусса
№ 11-20
11.
а)  б)
б) 
12.
а)  б)
б) 
13.
а) 

14.
 б)
б) 
15.
а)  б)
б) 
16.
a) 

17.
 б)
б) 
18.
 б)
б) 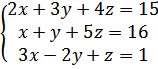
19.
 б)
б) 
20.


Тема 3. Элементы комбинаторики. [6], гл 5, п 1-3
№ 21-30.
21. Решить уравнение: 
22. Решить уравнение: 
23. Сколько способов распределения 3 одинаковых путевок в дом отдыха среди 5 рабочих цехов?
24. Сколько способов распределения путевок в санаторий, дом отдыха и в турбазу среди 5 рабочих цехов?
25. Решить уравнение: 
26. Сколько способов расставить 10 различных книг на полке?
27. Сколько трехзначных чисел можно образовать из цифр 2;8;7 без повторных цифр?
28. Сколько двухзначных чисел можно образовать из цифр 2;8;7 без повторных цифр?
29. Сколько четырехзначных чисел можно образовать из цифр 1;2;3;4 без повторных цифр?
30. Сколькими способами можно распределить 12 человек по бригадам по 6 человек в каждом?
Тема 4. Дифференциальное исчисление [1], гл. 7,8 § 1,2 [3], § 20,24
№ 31-40. Найти:
а) Производную и дифференциал функции
б) Наибольшее и наименьшее значение на [а;b]
31. a) 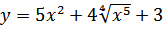
б) 
в) 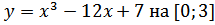
32. a) 
б) 
в) 
33. a) 
б) 
в) 
34. a) 
б) 
в) 
35. a) 
б) 
в) 
36. a) 
б) 
в) 
37. a) 
б) 
в) 
38. a) 
б) 
в) 
39. a) 
б) 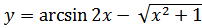
в) 
40. a) 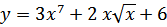
б) 
в) 
Тема 5. Интегральное исчисление [3] гл. 9,10 § 1,2 [1] гл. 10,11 § 1,2
№ 41-50. Найти интегралы в п. а), б), в) и площадь фигуры, ограниченный линиями в п. г)
41. a) 
б  )
)
в) 
г) 
42. a) 
б) 
в) 
г) 
43. a) 
б) 
 в)
в) 
г) y= 
44. а) 
б) 
в) 
г) 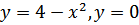
45. а) 
б) 
в) 
г)y= 
46. а) 
б) 
в) 
г) 
47. а) 
б) 
в) 
г) 
48. а) 
б) 
в) 
г) 
49. а) 
б) 
в) 
г) 
50. а) 
б) 
в) 
г) 
Тема 6. Дифференциальные уравнения [1], гл.12 § 1, 2
№ 51-60
Найти решение дифференциальных уравнений
а) общее,
б) частное
51.
 ; б)
; б) 
52.
 ; б)
; б) 
53.
а)  ;
; 
54.
 ;
; 
55.
 ;
; 
56.
а)  ;
; 
57.
 ;
; 
58.
 ;
; 
59.
 ;
; 
60.
 ;
; 
Тема 7. Элементы теории графов. [6], гл 4, п 1-4
№ 61-70. Для графа найти:
а) множество вершин, дуг и ребер, вид графа.
б) матрицу смежности вершин.
в) матрицу ребер и вершин.
г) маршруты длины 2.
| b |
| a |
61. 62.
| c |
| d |
65. 1 2 66. 1 2
3 4 4 3
67. 1 2 68. 1 2
4 3 3 4
69. 1 2 70. A b
4 3 d с
Дата публикования: 2014-10-20; Прочитано: 1155 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
