Решение прямоугольных систем линейных уравнений

Под прямоугольными понимают такие системы линейных уравнений, в которых число уравнений не равно числу неизвестных. Число уравнений может превышать число неизвестных, а может быть меньше его. Если в системе число уравнений превышает число неизвестных то возможны два случая. Первый: часть уравнений является следствием других уравнений, их можно отбросить, система станет или квадратной или число уравнений в ней будет меньше числа неизвестных. Второй: часть уравнений противоречит другим уравнениям, такая система несовместна, не имеет решения. Решение квадратных систем линейных уравнений подробно рассматривалось, поэтому рассмотрим решение систем, в которых число уравнений меньше числа неизвестных.

К составлению подобных систем приводит математическое моделирование многих экономических задач. Решение прямоугольных систем имеет свои особенности. В квадратных системах, т.е. системах, в которых число уравнений равно числу неизвестных, решением является единственный набор числовых значений неизвестных, обращающих все уравнения системы в тождества. В прямоугольных системах решение получается в виде соотношений между одними неизвестными, называемыми базисными, и другими, называемыми свободными. Поскольку свободные переменные могут принимать любые значения, а базисные переменные меняются в зависимости от них, то, по сути, прямоугольные системы имеют бесконечное множество числовых решений.

Рассмотрим пример. Найти решение системы линейных уравнений

при различных способах выбора базиса.

Выберем в качестве базисных неизвестные . Оставим их в левой части уравнений, а неизвестную перенесем в правую часть.

Эту систему можно решать как квадратную, например, методом Гаусса. Чтобы исключить из второго и третьего уравнений системы, прибавим ко второму первое, умноженное на 2, а к третьему - первое, умноженное на 4.

Чтобы исключить из третьего уравнения, прибавим к нему второе, умноженное на (-9).

Разделим обе части третьего уравнения на (-17) и найдем . Из второго уравнения найдем . Из первого уравнения

.

Итак, решение системы при первом способе выбора базиса:

Для проверки найденное решение подставим во все уравнения исходной системы.

Раскрывая скобки и приводя подобные, убеждаемся, что все уравнения системы обращаются в тождества.

Выберем теперь в качестве базисных переменные . Перенесем в левую, a 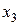- в правую часть полученного решения.

Запишем полученную систему в матричном виде:

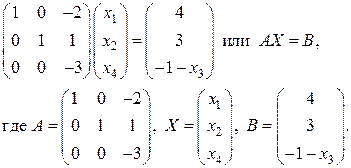
Ее решение , т.к. матрица А отличается от единичной одним столбцом, то обратная для нее находится легко по правилу, сформулированному в параграфе 2.2 раздела I:

Поэтому

Сделав проверку, выпишем вид решения при втором способе выбора базиса:

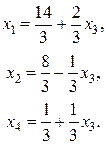
Чтобы найти вид решения при базисных переменных перепишем найденное решение так:

или .

Решая аналогично предыдущему шагу, находим

Наконец, выбираем в качестве базисных неизвестные .

Преобразуем предыдущее решение:

.

Решая выписанное матричное уравнение, найдем