Методы интегрирования. 1. Формула интегрирования по частям для определённого интеграла

1. Формула интегрирования по частям для определённого интеграла. Пусть функции 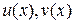– непрерывно дифференцируемые функции на промежутке 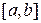, тогда справедливо равенство

. (12)

Равенство (12) называют формулой интегрирования по частям. Рассмотрим некоторые примеры вычисления определённых интегралов при помощи этой формулы. Основные типы интегралов, которые вычисляются только с помощью интегрирования по частям, уже были рассмотрены в примерах к предыдущему заданию. В этом пункте рассмотрим дополнительно ещё несколько интегралов такого вида.

Пример. Вычислим . Применив формулу (11), получим = = – = – = (применим ещё раз формулу (11)) = = –

– = – – .

Следовательно, получили уравнение относительно исходного интеграла – , из которого находим, что или = = .

Пример. Вычислим с помощью формулы интегрирования по частям (применим ещё раз формулу интегрирования по частям) =

= = =

2. Замена переменной в определённом интеграле. Пусть функция непрерывна на промежутке 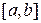, 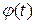непрерывно дифференцируема на промежутке и Тогда справедливо равенство

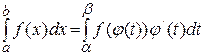. (13)

Пример. Вычислим интеграл с помощью формулы (13). Сделаем в этом интеграле замену переменной , тогда , . Продифференцировав последнее равенство, получим или . Пределы интегрирования по новой переменной находим из формулы замены , подставляя сначала нижний предел интегрирования 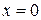, а затем верхний предел интегрирования . После этой замены получаем = = = = = = .