Эндогенные и экзогенные переменные

Эндогенные переменные: Переменные, значения которых изменяются только внутри моделируемой системы и никак не связаны с изменениями во внешней среде. Иными словами, значения этих переменных вычисляются моделями и обычно являются выходными (зависимыми).

Экзогенные переменные: Величины, характеризующие моделируемые объекты в экономическом анализе, рассчитываемые или определяемые вне модели. Иными словами, это переменные, значения которых известны заранее и которые могут использоваться в качестве входных (независимых). Например, в прогнозировании экзогенными переменными являются наблюдения прошлых значений временного ряда; в задаче классификации таковые могут быть как входными, так и выходными, поскольку как сами классы, так и параметры классифицируемых объектов должны быть известны заранее. Важным свойством экзогенных переменных является то, что при изменении параметров модели они не изменяются.

ОЦЕНКА ПАРАМЕТРОВ КЛАССИЧЕСКОЙ РЕГРЕССИОННОЙ МОДЕЛИ МЕТОДОМ НАЙМЕНЬШИХ КВАДРАТОВ

Введем обозначения: 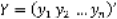− матрица-столбец, или вектор, значений зависимой переменной размера n;

свободный член умножается на фиктивную переменную принимающее значение 1.

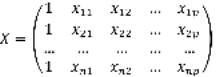
- матрица значений объясняющих переменных, или матрица плана размера

− матица-столбец, или вектор, параметров размера ; − матица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера n.

Модель в матричной форме:

Оценкой этой модели по выборке является уравнение

где

Для оценки вектора неизвестных параметров β применим метод наименьших квадратов. Так как произведение транспонированной матрицы на саму матрицу

(1)

то условие минимизации остаточной суммы квадратов запишется в виде:

(2)

Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. (Xb) =b X; после раскрытия скобок получим:

Произведение есть матрица размером , т.е. величина скалярная, следовательно, оно не меняется при транспонировании, т.е. . Поэтому условие минимизации (2) примет вид:

(3)

На основании необходимого условия основания экстремума функции нескольких переменных , представляющей (2), необходимо приравнять нулю частные производные по этим переменным или в матричной форме - вектор частных производных

Для вектора частных производных доказаны следующие формулы

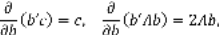
где b и c – вектор-столбцы; A – симметрическая матрица, в которой элементы, расположенные симметрично относительно главной диагонали, равны.

Поэтому, полагая , а матрицу , найдем

получаем систему нормальных уравнений в матричной форме для определения вектора b:

Найдем матрицы, входящие в это уравнение Матрица представляет собой сумму первых степеней, квадратов и попарных произведений n наблюдений объясняющих переменных:

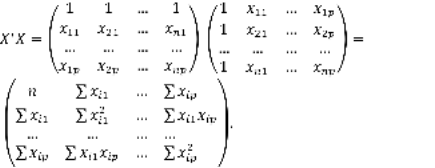(4)

Матрица есть вектор произведений n наблюдений объясняющих и зависимой переменных:

(5)

В частном случае из рассматриваемого матричного уравнения с учетом (4) и (5) для одной объясняющей переменной (p=1) можно получить систему нормальных уравнений. Действительно, в этом случае матричное уравнение примет вид:

откуда непосредственно следует система нормальных уравнений для определения параметров линейной регрессии

Теперь разделив обе части уравнения на n, получим систему

откуда получаем , и подставляя в (уравнение регрессии линейного вида), получаем:

, или

Коэффициент b₁ называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии) Y по X, который показывает на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на дну еденицу.

,

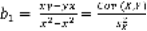где – выборочная дисперсия переменной X:

– выборочный корреляционный момент или выборочная коварияция:

.