Корень из комплексного числа. Основная теорема алгебры

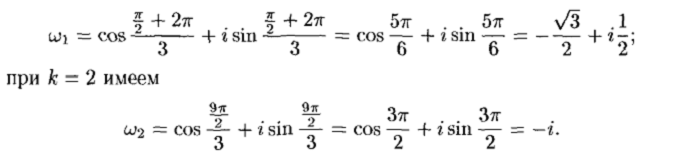
Основная теорема алгебры. Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.

Следствие 1. Любой многочлен степени с комплексными коэффициентами можно представить в виде произведения линейных двучленов:

=

где — корни многочлена кратности соответственно, причем . Другими словами, многочлен n-й степени имеет ровно корней, если каждый корень считать столько раз, какова его кратность.

Следствие 2. Если многочлены и , степени которых не превосходят , имеют равные значения более чем при п различных значениях переменной , то эти многочлены равны: .