 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Непрерывная и дискретная информация
|
|
Чтобы сообщение было передано от источника к получателю, необходима некоторая материальная субстанция – носитель информации. Сообщение, передаваемое с помощью носителя, назовем сигналом. В общем случае сигнал – это изменяющийся во времени физический процесс. Такой процесс может содержать различные характеристики (например, при передаче электрических сигналов могут изменяться напряжение и сила тока). Та из характеристик, которая используется для представления сообщений, называется параметром сигнала.
В случае, когда параметр сигнала принимает последовательное во времени конечное число значений (при этом все они могут быть пронумерованы), сигнал называется дискретным, а сообщение, передаваемое с помощью таких сигналов – дискретным сообщением. Информация, передаваемая источником, в этом случае также называется дискретной. Если же источник вырабатывает непрерывное сообщение (соответственно параметр сигнала – непрерывная функция от времени), соответствующая информация называется непрерывной. Пример дискретного сообщения – процесс чтения книги, информация в которой представлена текстом, т.е. дискретной последовательностью отдельных значков (букв). Примером непрерывного сообщения служит человеческая речь, передаваемая модулированной звуковой волной; параметром сигнала в этом случае является давление, создаваемое этой волной в точке нахождения приемника – человеческого уха.
Непрерывное сообщение может быть представлено непрерывной функцией f (t), заданной на некотором отрезке [а, b] (рис. 1. 2, а). Непрерывное сообщение можно

преобразовать в дискретное (такая процедура называется дискретизацией). Для этого из бесконечного множества значений этой функции (параметра сигнала) выбирается их определенное число, которое приближенно может характеризовать остальные значения. Один из способов такого выбора состоит в следующем. Область определения функции разбивается точками t1, t2,..., tn на промежутки равной длины  (равномерная дискретизация), и непрерывная функция заменяется импульсной с некоторой короткой и одинаковой продолжительностью импульсов, амплитуда каждого из которых принимается постоянной и равной значению функции в указанных точках (рис. 1.2, б). Полученная таким образом импульсная функция является дискретным представлением непрерывной функции, точность которого можно неограниченно улучшать (по крайней мере теоретически) путем уменьшения длин отрезков разбиения области значений аргумента.
(равномерная дискретизация), и непрерывная функция заменяется импульсной с некоторой короткой и одинаковой продолжительностью импульсов, амплитуда каждого из которых принимается постоянной и равной значению функции в указанных точках (рис. 1.2, б). Полученная таким образом импульсная функция является дискретным представлением непрерывной функции, точность которого можно неограниченно улучшать (по крайней мере теоретически) путем уменьшения длин отрезков разбиения области значений аргумента.
Таким образом, любое сообщение может быть представлено как дискретное, иначе говоря, последовательностью знаков некоторого алфавита.
Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер – цифровая машина, т.е. внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки.
Вопрос о способах дискретизации непрерывно представленной информации и восстановления такой информации по ее дискретному представлению (так называемым «отсчетам») возник в технике электросвязи существенно раньше создания ЭВМ (в связи с разработкой устройств цифровой временной коммутации для телефонных станций). Теоретическую базу для его решения (в случае равномерной дискретизации) заложил в 1933 г. советский ученый В. А. Котельников, сформулировавший ставшую впоследствии классической теорему, носящую его имя.
Теорема Котельникова: если непрерывный сигнал имеет спектр, ограниченный сверху частотой  , то этот сигнал полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал
, то этот сигнал полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал 
Например, сигнал звукового сопровождения в телевизионном канале ограничен сверху частотой 12 кГц. Если выбрать интервал дискретизации для этого сигнала не более чем  то непрерывный сигнал может (теоретически) быть восстановлен после дискретизации точно. Примечание «теоретически» означает, что конкретные технические устройства могут иметь дополнительные ограничения, которые здесь обсуждаться не будут. Кроме того, реальные непрерывные сигналы, подлежащие дискретизации и последующему восстановлению, имеют, как правило, неограниченные по частоте спектры, хотя высокочастотная составляющая быстро стремится к нулю с ростом частоты. Такие сигналы могут быть восстановлены по своим дискретным отсчетам лишь приближенно. Придискретизации в таких случаях вводят некоторую граничную частоту, за пределами которой высокочастотными составляющими просто пренебрегают. Так, при передаче телефонного сигнала такую частоту часто берут равной 3,4 кГц, что соответствует интервалу дискретизации
то непрерывный сигнал может (теоретически) быть восстановлен после дискретизации точно. Примечание «теоретически» означает, что конкретные технические устройства могут иметь дополнительные ограничения, которые здесь обсуждаться не будут. Кроме того, реальные непрерывные сигналы, подлежащие дискретизации и последующему восстановлению, имеют, как правило, неограниченные по частоте спектры, хотя высокочастотная составляющая быстро стремится к нулю с ростом частоты. Такие сигналы могут быть восстановлены по своим дискретным отсчетам лишь приближенно. Придискретизации в таких случаях вводят некоторую граничную частоту, за пределами которой высокочастотными составляющими просто пренебрегают. Так, при передаче телефонного сигнала такую частоту часто берут равной 3,4 кГц, что соответствует интервалу дискретизации 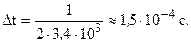
Существенно, что теорема Котельникова не просто «теорема о возможности», но носит конструктивный характер. Восстановление непрерывного сигнала по его дискретному образу реализуется путем суммирования ряда

В завершение отметим, что существуют и принципиально другие, нецифровые, вычислительные машины – аналоговые ЭВМ. Они используются обычно для решения задач специального характера и широкой публике практически неизвестны. Эти ЭВМ в принципе не нуждаются в дискретизации входной информации, так как ее внутреннее представление у них непрерывно. В этом случае все наоборот – если внешняя информация дискретна, то ее «перед употреблением» необходимо преобразовать в непрерывную.
Единицы количества информации: вероятностный и объемный подходы. Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти одновременно. В конце 1940 гг. один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.
Вероятностный подход. Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей N граней (наиболее распространенным является случай шестигранной кости: N = 6). Результатом данного опыта может быть выпадение грани с одним из следующих знаков: 1, 2,..., N
Введем в рассмотрение численную величину, измеряющую неопределенность – энтропию (обозначим ее H). Величины N и Н связаны между собой некоторой функциональной зависимостью:
H = f(N), (1.1)
а сама функция/является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N = 1, 2,..., 6.
Рассмотрим процедуру бросания кости более подробно:
1) готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее Н 1;
2) кость брошена; информация об исходе данного опыта получена; обозначим количество этой информации через I;
3) обозначим неопределенность данного опыта после его осуществления через H2.
За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей «до» и «после» опыта:
I = H1 – H2.
Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята (H2 = 0), и, таким образом, количество полученной информации совпадает с первоначальной энтропией. Иначе говоря, неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта.
Следующим важным моментом является определение вида функции f в формуле (1.1). Если варьировать число граней N ичисло бросаний кости (обозначим эту величину через М), то общее число исходов (векторов длины М, состоящих из знаков 1, 2,..., N) будет равно N встепени М:
X=NM. (1..2)
Так, в случае двух бросаний кости с шестью гранями имеем Х= 62 = 36. Фактически каждый исход X есть некоторая пара (X 1, Х 2 ), где X 1и Х 2 - соответственно исходы первого и второго бросаний (X –общее число таких пар).
Ситуацию с бросанием кости М раз можно рассматривать как некую сложную систему, состоящую из независимых друг от друга подсистем - «однократных бросаний кости». Энтропия такой системы в М раз больше, чем энтропия одной системы (так называемый «принцип аддитивности энтропии»):
f(6M) = Mf(6).
Данную формулу можно распространить и на случай любого N:
f{NM) = Mf(N). (1.3)
Прологарифмируем левую и правую части формулы (1.2): ln Х = M ln N, M = ln X/ ln N.
Подставляем полученное для М значение в формулу (1.3): 
Обозначив через K положительную константу, получим f(X) = К ln Х, или, с учетом (1.1), Н = K ln N. Обычно принимают К= 1/ln2. Таким образом,
H=log2 N. (1.4)
Выражение (1.4) – формула Хартли.
Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, Н будет равно единице при N = 2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты, при котором возможны два исхода: «орел» и «решка»). Такая единица количества информации называется «бит».
Все N исходов рассмотренного выше опыта являются равновероятными и поэтому можно считать, что на «долю» каждого исхода приходится одна N -я часть общей неопределенности опыта: (log2N)/N. При этом вероятность i -го исхода Р i равняется, очевидно, 1 /N.
Таким образом,
 (1.5)
(1.5)
Формула (1.5) принимается за меру энтропии и в случае, когда вероятности различных исходов опыта неравновероятны (т.е. Pi могут быть различны). Формула (1.5) называется формулой Шеннона.
Вкачестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака «пробел» для разделения слов. По формуле (1.4)
Н = log2 34 = 5 бит.
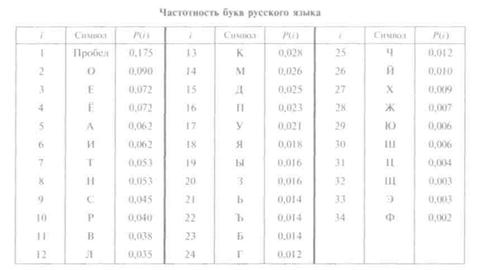
Однако в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. В табл. 1.1 приведены вероятности частоты употребления различных знаков русского алфавита, полученные на основе анализа очень больших по объему текстов.
Воспользуемся для подсчета H формулой (1.5): 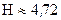 бит. Полученное значение Н, как и можно было предположить, меньше вычисленного ранее. Величина Н, вычисляемая по формуле (1.4), является максимальным количеством информации, которое могло бы приходиться на один знак.
бит. Полученное значение Н, как и можно было предположить, меньше вычисленного ранее. Величина Н, вычисляемая по формуле (1.4), является максимальным количеством информации, которое могло бы приходиться на один знак.
Аналогичные подсчеты Н можно провести и для других языков, например использующих латинский алфавит, – английского, немецкого, французского и др. (26 различных букв и «пробел»). По формуле (1.4) получим
H = log227» 4,76 бит.
Как и в случае русского языка, частота появления тех или иных знаков неодинакова. Если расположить все буквы данных языков в порядке убывания вероятностей, то получим такие последовательности:
английский язык: «пробел», Е, Т, А, О, N, R,...
немецкий язык: «пробел», Е, N, I, S, Т, R,...
французский язык: «пробел», Е, S, A, N, I, T,...
Рассмотрим алфавит, состоящий из двух знаков: 0 и 1. Если считать, что со знаками 0 и 1 в двоичном алфавите связаны одинаковые вероятности их появления (Р(0) = Р(1) = 0,5), то количество информации на один знак при двоичном кодировании
H = log22 = 1 бит.
Таким образом, количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.
Объемный подход. В двоичной системе счисления знаки 0 и 1 будем называть битами (от английского выражения Binary digits – двоичные цифры). Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния. В компьютере бит является наименьшей возможной единицей информации.
Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации, подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, в частности, невозможно нецелое число битов (в отличие от вероятностного подхода).
Для удобства использования введены и более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми знаков содержит один байт информации, 1024 байта образуют килобайт (Кбайт), 1024 килобайта – мегабайт (Мбайт), а 1024 мегабайта – гигабайт (Гбайт).
Между вероятностным и объемным количеством информации соотношение неоднозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускает его измерение в объемном смысле. Далее, если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом кибернетическое количество информации не может быть больше объемного.
В дальнейшем тексте данного учебника практически всегда количество информации понимается в объемном смысле.
Информация: более широкий взгляд. Как ни важно измерение информации, нельзя сводить к нему все связанные с этим понятием проблемы. При анализе информации социального (в широким смысле) происхождения на первый план могут выступить такие ее свойства, как истинность, своевременность, ценность, полнота и т.д. Их невозможно оценить ни уменьшением неопределенности (вероятностный подход), ни числом символов (объемный подход). Обращение к качественной стороне информации породило иные подходы к ее оценке. При аксиологическом подходе стремятся исходить из ценности, практической значимости информации, т.е. качественных характеристик, значимых в социальной системе. При семантическом подходе информация рассматривается с точки зрения как формы, так и содержания. При этом информацию связывают с тезаурусом, т.е. полнотой систематизированного набора данных о предмете информации. Отметим, что эти подходы не исключают количественного анализа, но он становится существенно сложнее и должен базироваться на современных методах математической статистики.
Понятие информации нельзя-считать лишь техническим, междисциплинарным и даже наддисциплинарным термином. Информация – это фундаментальная философская категория. Дискуссии ученых о философских аспектах информации надежно показали несводимость информации ни к одной из этих категорий. Концепции и толкования, возникающие на пути догматических подходов, оказываются слишком частными, односторонними, не охватывающими всего объема этого понятия.
Попытки рассмотреть категорию информации с позиций основного вопроса философии привели к возникновению двух противостоящих концепций – так называемых атрибутивной и функциональной. «Атрибутисты» квалифицируют информацию как свойство всех материальных объектов, т.е. как атрибут материи. «Функционалисты» связывают информацию лишь с функционированием сложных, самоорганизующихся систем. Оба подхода, скорее всего, неполны. Дело в том, что природа сознания по сути своей является информационной, т.е. сознание – менее общее понятие по отношению к категории «информация». Нельзя признать корректными попытки сведения более общего понятия к менее общему. Таким образом, информация и информационные процессы, если иметь в виду решение основного вопроса философии, опосредуют материальное и духовное, т.е. вместо классической постановки этого вопроса получается два новых: о соотношении материи и информации и о соотношении информации и сознания (духа).
Можно попытаться дать философское определение информации с помощью указания на связь определяемого понятия с категориями отражения и активности. Информация есть содержание образа, формируемого в процессе отражения. Активность входит в это определение в виде представления о формировании некоего образа в процессе отражения некоторого субъект-объектного отношения. При этом не требуется указания на связь информации с материей, поскольку как субъект, так и объект процесса отражения могут принадлежать как к материальной, так и к духовной сфере социальной жизни. Однако существенно подчеркнуть, что материалистическое решение основного вопроса философии требует признания необходимости существования материальной среды – носителя информации в процессе такого отражения. Итак, информацию следует трактовать как имманентный (неотъемлемо присущий) атрибут материи, необходимый момент ее самодвижения и саморазвития. Эта категория приобретает особое значение применительно к высшим формам движения материи – биологической и социальной.
Данное выше определение охватывает важнейшие характеристики информации. Оно не противоречит тем знаниям, которые накоплены по этой проблематике, а наоборот, является выражением наиболее значимых.
Современная практика психологии, социологии, информатики диктует необходимость перехода к информационной трактовке сознания. Такая трактовка оказывается чрезвычайно плодотворной и позволяет, например, рассмотреть с общих позиций индивидуальное и общественное сознание. Генетически индивидуальное и общественное сознание неразрывны и в то же время общественное сознание не есть простая сумма индивидуальных, поскольку оно включает информационные потоки и процессы между индивидуальными сознаниями.
В социальном плане человеческая деятельность предстает как взаимодействие реальных человеческих коммуникаций с предметами материального мира. Поступившая извне к человеку информация является отпечатком, снимком сущностных сил природы или другого человека. Таким образом, с единых методологических позиций может быть рассмотрена деятельность индивидуального и общественного сознания, экономическая, политическая, образовательная деятельность различных субъектов социальной системы.
Определение информации как философской категории не только затрагивает физические аспекты существования информации, но и фиксирует ее социальную значимость.
Одной из важнейших черт функционирования современного общества выступает его информационная оснащенность. В ходе своего развития человеческое общество прошло через пять информационных революций. Первая из них была связана с появлением языка, вторая – письменности, третья – книгопечатания, четвертая – телесвязи, и, наконец, пятая – компьютеров (а также магнитных и оптических носителей хранения информации). Каждый раз новые информационные технологии поднимали информированность общества на несколько порядков, радикально меняя объем и глубину знания, а вместе с этим и уровень культуры в целом.
Одна из целей философского анализа понятия информации – указать место информационных технологий в развитии форм движения материи, в прогрессе человечества и, в том числе, в развитии разума как высшей отражательной способности материи. На протяжении десятков тысяч лет сфера разума развивалась исключительно через общественную форму сознания. С появлением компьютеров начались разработки систем искусственного интеллекта, идущих по пути моделирования общих интеллектуальных функций индивидуального сознания.
Информация и физический мир. Известно большое количество работ, посвященных физической трактовке информации. Эти работы в значительной мере построены на основе аналогии формулы Больцмана, описывающей энтропию статистической системы материальных частиц, и формулы Хартли.
Заметим, что при всех выводах формулы Больцмана явно или неявно предполагается, что макроскопическое состояние системы, к которому относится функция энтропии, реализуется на микроскопическом уровне как сочетание механических состояний очень большого числа частиц (молекул), образующих систему. В задачах кодирования и передачи информации, для решения которых Хартли и Шенноном была развита вероятностная мера информации, использовалось очень узкое техническое понимание информации, почти не имеющее отношения к полному объему этого понятия. Таким образом, большинство рассуждений, использующих термодинамические свойства энтропии применительно к информации нашей реальности, носят спекулятивный характер. В частности, являются необоснованными использование понятия «энтропия» для систем с конечным и небольшим числом состояний, а также попытки расширительного методологического толкования результатов теории вне довольно примитивных механических моделей, для которых они были получены.
Информацию следует считать особым видом ресурса, при этом имеется в виду толкование «ресурса» как запаса неких знаний материальных предметов или энергетических, структурных или каких-либо других характеристик предмета. В отличие от ресурсов, связанных с материальными предметами, информационные ресурсы являются неистощимыми и предполагают существенно иные методы воспроизведения и обновления, чем материальные ресурсы.
Рассмотрим некоторый набор свойств информации:
• запоминаемость;
• передаваемость;
• воспроизводимость;
• преобразуемость;
• стираемость.
Запоминаемость – одно из самых важных свойств. Запоминаемую информацию будем называть макроскопической (имея в виду пространственные масштабы запоминающей ячейки и время запоминания). Именно с макроскопической информацией мы имеем дело в реальной практике.
Передаваемость информации с помощью каналов связи (в том числе с помехами) хорошо исследована в рамках теории информации К. Шеннона. В данном случае имеется в виду несколько иной аспект – способность информации к копированию, т.е. к тому, что она может быть «запомнена» другой макроскопической системой и при этом останется тождественной самой себе. Очевидно, что количество информации не должно возрастать при копировании.
Воспроизводимость информации тесно связана с ее передаваемостью и не является ее независимым базовым свойством. Если передаваемость означает, что не следует считать существенными пространственные отношения между частями системы, между которыми передается информация, то воспроизводимость характеризует неиссякаемость и неистощимость информации, т.е. что при копировании информация остается тождественной самой себе.
Фундаментальное свойство информации – преобразуемость. Оно означает, что информация может менять способ и форму своего существования. Копируемость есть разновидность преобразования информации, при котором ее количество не меняется. В общем случае количество информации в процессах преобразования меняется, но возрастать не может.
Свойство стираемости информации также не является независимым. Оно связано с таким преобразованием информации (передачей), при котором ее количество уменьшается и становится равным нулю.
Данных свойств информации недостаточно для формирования ее меры, так как они относятся к физическому уровню информационных процессов.
Подводя итог сказанному, отметим, что предпринимаются (но отнюдь не завершены) усилия ученых, представляющих самые разные области знания, построить единую теорию, которая призвана формализовать понятие информации и информационного процесса, описать превращения информации в процессах самой разной природы. Движение информации есть сущность процессов управления, которые суть проявление имманентной активности материи, ее способности к самодвижению. С момента возникновения кибернетики управление рассматривается применительно ко всем формам движения материи, а не только к высшим (биологической и социальной). Многие проявления движения в неживых – искусственных (технических) и естественных (природных) – системах также обладают общими признаками управления, хотя их исследуют в химии, физике, механике в энергетической, а не в информационной системе представлений. Информационные аспекты в таких системах составляют предмет новой междисциплинарной науки – синергетики.
Высшей формой информации, проявляющейся в управлении в социальных системах, являются знания. Это наддисциплинарное понятие, широко используемое в педагогике и исследованиях по искусственному интеллекту, также претендует на роль важнейшей философской категории. В философском плане познание следует рассматривать как один из функциональных аспектов управления. Такой подход открывает путь к системному пониманию генезиса процессов познания, его основ и перспектив.
Кодирование информации. Абстрактный алфавит. Информация передается в виде сообщений. Дискретная информация записывается с помощью некоторого конечного набора знаков, которые будем называть буквами, не вкладывая в это слово привычного ограниченного значения (типа «русские буквы» или «латинские буквы»). Буква в данном расширенном понимании – любой из знаков, которые некоторым соглашением установлены для общения. Например, при привычной передаче сообщений на русском языке такими знаками будут русские буквы – прописные и строчные, знаки препинания, пробел; если в тексте есть числа – то и цифры. Вообще буквой будем называть элемент некоторого конечного множества (набора) отличных друг от друга знаков. Множество знаков, в котором определен их порядок, назовем алфавитом (общеизвестен порядок знаков в русском алфавите: А, Б,..., Я).
Рассмотрим некоторые примеры алфавитов.
1. Алфавит прописных русских букв:
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
2. Алфавит клавиатурных символов ПЭВМ IBM (русифицированная клавиатура):
1234567890–=
~!@#$%^&*()_+
qwertyuiop[]
QWERTYUIOP{}
asdfghjkl;:"
ASDFGHJKL:«»
zxcvbnm,./
ZXCVBNM<>?
йцукенгшщзхъ
ЙЦУКЕНГШЩЗХЪ
фывапролджэ
ФЫВАПРОЛДЖЭ
ячсмитьбю
ЯЧСМИТЬБЮ
3. Алфавит знаков правильной шестигранной игральной кости:

4. Алфавит арабских цифр:
5. Алфавит шестнадцатеричных цифр:
0123456789ABCDEF
Этот пример, в частности, показывает, что знаки одного алфавита могут образовываться из знаков других алфавитов.
6. Алфавит двоичных цифр:
0 1
Алфавит 6 является одним из примеров так называемых «двоичных» алфавитов, т. е. алфавитов, состоящих из любых двух знаков. Другими примерами являются двоичные алфавиты: «точка», «тире» (×¾); «плюс», «минус» (+ –).
7. Алфавит прописных латинских букв:
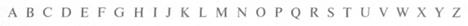
8. Алфавит римской системы счисления:
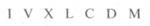
9. Алфавит языка блок-схем изображения алгоритмов:

10. Алфавит языка программирования Паскаль (см. гл. 3).
Кодирование и декодирование. В канале связи сообщение, составленное из символов (букв) одного алфавита, может преобразовываться в сообщение из символов (букв) другого алфавита. Правило, описывающее однозначное соответствие букв алфавитов при таком преобразовании, называют кодом. Саму процедуру преобразования сообщения называют перекодировкой. Подобное преобразование сообщения может осуществляться в момент поступления сообщения от источника в канал связи (кодирование) и в момент приема сообщения получателем (декодирование). Устройства, обеспечивающие кодирование и декодирование, будем называть соответственно кодировщиком и декодировщиком. На рис. 1.3 приведена схема, иллюстрирующая процесс передачи сообщения в случае перекодировки, а также воздействия помех.
Рассмотрим некоторые примеры кодов.
1. Азбука Морзе в русском варианте (алфавиту, составленному из алфавита русских заглавных букв и алфавита арабских цифр, ставится в соответствие алфавит Морзе):

Рис. 1.3. Процесс передачи сообщения от источника к приемнику
2. Код Трисиме (знакам латинского алфавита ставятся в соответствие комбинации из трех знаков: 1, 2, 3):

Код Трисиме является примером так называемого равномерного кода (такого, в котором все кодовые комбинации содержат одинаковое число знаков – в данном случае три). Пример неравномерного кода – азбука Морзе.
Кодирование чисел знаками различных систем счисления будет рассмотрено далее.
Международные системы байтового кодирования. Информатика и ее приложения интернациональны. Это связано как с объективными потребностями человечества в единых правилах и законах хранения, передачи и обработки информации, так и с тем, что в этой сфере деятельности (особенно в ее прикладной части) заметен приоритет одной страны, которая благодаря этому получает возможность «диктовать моду».
Компьютер считают универсальным преобразователем информации. Тексты на естественных языках и числа, математические и специальные символы – одним словом все, что в быту или в профессиональной деятельности может быть необходимо человеку, должно иметь возможность быть введенным в компьютер.
В силу безусловного приоритета двоичной системы счисления при внутреннем представлении информации в компьютере кодирование «внешних» символов основывается на сопоставлении каждому из них определенной группы двоичных знаков. При этом из технических соображений и из соображений удобства кодирования-декодирования следует пользоваться равномерными кодами, т.е. двоичными группами равной длины.
Попробуем подсчитать наиболее короткую длину такой комбинации с точки зрения человека, заинтересованного в использовании лишь одного естественного алфавита – скажем, английского: 26 букв следует умножить на 2 (прописные и строчные) – итого 52; 10 цифр; будем считать, 10 знаков препинания; 10 разделительных знаков (три вида скобок, пробел и др.); знаки привычных математических действий; несколько специальных символов (типа #, $, & и др.) – итого примерно 100. Точный подсчет здесь не нужен, поскольку нам предстоит решить простейшую задачу: имея равномерный код из групп по N двоичных знаков, сколько можно образовать разных кодовых комбинаций? Ответ очевиден: К = 2N. Итак, при N = 6 К = 64 – явно мало, при N = 7 К = 128 – вполне достаточно.
Однако для кодирования нескольких (хотя бы двух) естественных алфавитов (плюс все отмеченные выше знаки) и этого недостаточно. Минимально достаточное значение N вэтом случае 8; имея 256 комбинаций двоичных символов, вполне можно решить указанную задачу. Поскольку 8 двоичных символов составляют 1 байт, то говорят о системах «байтового» кодирования.
Наиболее распространены две такие системы: EBCDIC (Extended Binary Coded Decimal Interchange Code) и ASCII (American Standard Cod Information Interchange). Первая исторически тяготеет к «большим» машинам, вторая чаще используется на мини- и микроЭВМ (в том числе и на персональных компьютерах). Ознакомимся подробнее именно с ASCII, созданной в 1963 г.
В своей первоначальной версии это система семибитного кодирования. Она ограничивалась одним естественным алфавитом (английским), цифрами и набором различных символов, включающих «символы пишущей машинки» (привычные знаки препинания, знаки математических действий и др.) и «управляющие символы». Примеры последних легко найти на клавиатуре компьютера: для микроЭВМ, например, DEL – знак удаления символа.
В следующей версии фирма IBM перешла на расширенную 8-битную кодировку. В ней первые 128 символов совпадают с исходными и имеют коды со старшим битом, равным нулю, а остальные коды отданы под буквы некоторых европейских языков, в основе которых лежит латиница, греческие буквы, математические символы (например знак квадратного корня) и символы псевдографики. С помощью последних можно создавать таблицы, несложные схемы и др.
Для представления букв русского языка (кириллицы) в рамках ASCII было предложено несколько версий. Первоначально был разработан стандарт под названием КОИ-7, оказавшийся по ряду причин крайне неудачным; ныне он практически не используется.
В табл. 1.6 приведена часто используемая в нашей стране модифицированная альтернативная кодировка. В левую часть входят исходные коды ASCII, в правую часть (расширение ASCII) вставлены буквы кириллицы взамен букв немецкого, французского алфавитов (не совпадающих по написанию с английскими), греческих букв, некоторых специальных символов.
Знакам алфавита ПЭВМ ставятся в соответствие шестнадцатеричные числа по правилу: первая – номер столбца, вторая – номер строки. Например: английская «А» – код 41, русская «и» – код А8.
Одним из достоинств этой системы кодировки русских букв является их естественное упорядочение, т.е. номера букв следуют друг за другом в том же порядке, в каком сами буквы стоят в русском алфавите. Это очень существенно при решении ряда задач обработки текстов, когда требуется выполнить или использовать лексикографическое упорядочение слов.
Отметим, что даже 8-битная кодировка недостаточна для кодирования всех символов, которые хотелось бы иметь в расширенном алфавите. Все препятствия

Теоремы Шеннона. Ранее отмечалось, что при передаче сообщений по каналам связи могут возникать помехи, способные привести к искажению принимаемых знаков. Так, например, если вы попытаетесь в ветреную погоду передать речевое сообщению человеку, находящемуся от вас на значительном расстоянии, то оно может быть сильно искажено такой помехой, как ветер. Вообще передача сообщений при наличии помех является серьезной теоретической и практической задачей. Ее значимость возрастает в связи с повсеместным внедрением компьютерных телекоммуникаций, в которых помехи неизбежны. При работе с кодированной информацией, искажаемой помехами, можно выделить следующие основные проблемы: установление самого факта того, что произошло искажение информации; выяснение того, в каком конкретно месте передаваемого текста это произошло; исправление ошибки, хотя бы с некоторой степенью достоверности.
Помехи в передачи информации – вполне обычное дело во всех сферах профессиональной деятельности и в быту. Один из примеров был уже приведен, другие примеры – разговор по телефону, в трубке которого «трещит», вождение автомобиля в тумане и т.д. Чаще всего человек вполне справляется с каждой из указанных задач, хотя и не всегда отдает себе отчет, как он это делает (т.е. неалгоритмически, а исходя из каких-то ассоциативных связей). Известно, что естественный язык обладает большой избыточностью (в европейских языках – до 7%), чем объясняется большая помехоустойчивость сообщений, составленных из знаков алфавитов таких языков. Примером, иллюстрирующим устойчивость русского языка к помехам, может служить предложение «в словах все гласное заменено буквой о». Здесь 26% символов «поражены», однако это не приводит к потере смысла. Таким образом, в данном случае избыточность является полезным свойством.
Избыточность могла бы быть использована и при передаче кодированных сообщений в технических системах. Например, каждый фрагмент текста (предложение) передается трижды, и верным считается та пара фрагментов, которая полностью совпала. Однако большая избыточность приводит к большим временным затратам при передаче информации и требует большого объема памяти при ее хранении. Впервые теоретическое исследование эффективного кодирования предпринял К.Шеннон.
Первая теорема Шеннона декларирует возможность создания системы эффективного кодирования дискретных сообщений, у которой среднее число двоичных символов на один символ сообщения асимптотически стремится к энтропии источника сообщений (в отсутствии помех).
Задача эффективного кодирования описывается триадой:
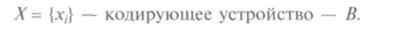
Здесь X, В – соответственно входной и выходной алфавит; под множеством х, можно понимать любые знаки (буквы, слова, предложения); В – множество, число элементов которого в случае кодирования знаков числами определяется основанием системы счисления (например, т = 2). Кодирующее устройство сопоставляет каждому сообщению х, из X кодовую комбинацию, составленную из ni символов множества В. Ограничением данной задачи является отсутствие помех. Требуется оценить минимальную среднюю длину кодовой комбинации.

Для решения данной задачи должна быть известна вероятность Pt появления сообщения xi, которому соответствует определенное количество символов и, алфавита В. Тогда математическое ожидание количества символов из В определится следующим образом:

Этому среднему числу символов алфавита В соответствует максимальная энтропия Нmax = n cplog т. Для обеспечения передачи информации, содержащейся в сообщениях X кодовыми комбинациями из В, должно выполняться условие Нmax ³ H(х), или n cplog m ³ –Pi log Pi. В этом случае закодированное сообщение имеет избыточность п ср ³ H(x)/ log m, nmin = H(x) / log m.
Коэффициент избыточности

Выпишем эти значения в виде табл. 1.7. Имеем:
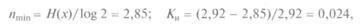
т. е. код практически не имеет избыточности. Видно, что среднее число двоичных символов стремится к энтропии источника сообщений.
Вторая теорема Шеннона гласит, что при наличии помех в канале всегда можно найти такую систему кодирования, при которой сообщения будут переданы с заданной достоверностью. При наличии ограничения пропускная способность канала должна превышать производительность источника сообщений. Таким образом, вторая теорема Шеннона устанавливает принципы помехоустойчивого кодирования. Для дискретного канала с помехами теорема утверждает, что если скорость создания сообщений меньше или равна пропускной способности канала, то существует код, обеспечивающий передачу со сколь угодно малой частотой ошибок.
Доказательство теоремы основывается на следующих рассуждениях. Первоначально последовательность Х= { хi } кодируется символами из В так, что достигается максимальная пропускная способность (канал не имеет помех). Затем в последовательность из В длины п вводится r дополнительных символов и по каналу передается новая последовательность из n + r символов. Эти r дополнительных символов обеспечивают избыточность кодирования информации и позволяют противодействовать помехам. Число возможных последовательностей длины п + r больше числа возможных последовательностей длины п. Множество всех последовательностей длины п + r может быть разбито на и подмножеств, каждому из которых сопоставлена одна из последовательностей длины п. Воздействие помехи на последовательность из n + r символов выводит ее из соответствующего подмножества с вероятностью, зависящей от r. Это позволит определить на приемной стороне канала, какому подмножеству принадлежит искаженная помехами принятая последовательность длины п + r, и тем самым восстановить исходную последовательность длины п.
Эта теорема не дает конкретного метода построения кода, но указывает на пределы достижимого в создании помехоустойчивых кодов, стимулирует поиск новых путей решения этой проблемы.
Дата публикования: 2014-10-19; Прочитано: 10191 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
