 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение типовых задач. 1. Оценить следующую структурную модель на идентификацию:
|
|
Пример 1. Требуется:
1. Оценить следующую структурную модель на идентификацию:
 ,
,
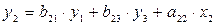 ,
,
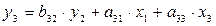 .
.
2. Исходя из приведенной формы модели уравнений
 ,
,
 ,
,
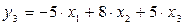 ,
,
найти структурные коэффициенты модели.
Решение:
1. Модель имеет три эндогенные (y1, y2, y3) и три экзогенные (x1, x2, x3) переменные.
Проверим каждое уравнение системы на необходимые (H) и достаточное (Д) условия идентификации.
Первое уравнение:
Н: эндогенных переменных – 2 (y1, y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют y2 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| y2 | x2 | |
| Второе | -1 | a22 |
| Третье | b32 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Второе уравнение:
Н: эндогенных переменных – 3 (y1, y2, y3),
отсутствующих экзогенных – 2 (x1, x3).
Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо.
Д: во втором уравнении отсутствуют x1 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| x1 | x3 | |
| Первое | a11 | a13 |
| Третье | a31 | a33 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.
Третье уравнение:
Н: эндогенных переменных – 2 (y2, y3),
отсутствующих экзогенных – 1 (x2).
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в третьем уравнении отсутствуют y1 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| y1 | x2 | |
| Первое | -1 | 0 |
| Второе | B21 | a22 |
 .
.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо.
Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.
2. Вычислим структурные коэффициенты модели:
1) из третьего уравнения приведенной формы выразим x2 (так как его нет в первом уравнении структурной формы):
 .
.
Данное выражение содержит переменные y3, x1 и x3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x2 в первое уравнение приведенной формы модели (ПФМ):
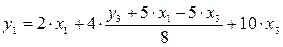 Þ
Þ  – первое уравнение СФМ;
– первое уравнение СФМ;
2) во втором уравнении СФМ нет переменных x1 и x3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Первый этап: выразим x1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:
 .
.
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует x3, которого нет в СФМ.
Выразим x3 из третьего уравнения ПФМ:
 .
.
Подставим его в выражение x1:
 ;
;
 .
.
Второй этап: аналогично, чтобы выразить x3 через искомые y1, y3 и x2, заменим в выражении x3 значение x1 на полученное из первого уравнения ПФМ:
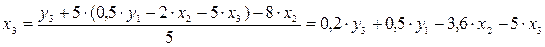 .
.
Следовательно,  .
.
Подставим полученные x1 и x3 во второе уравнение ПФМ:
 Þ
Þ
 – второе уравнение СФМ.
– второе уравнение СФМ.
Это уравнение можно получить из ПФМ иным путем. Суммируя все уравнения, получим
 ,
,
 ,
,
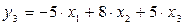

Далее из первого и второго уравнений ПФМ исключим x1, домножив первое уравнение на 3, а второе – на (-2) и просуммировав их:
 ,
,

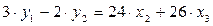
Затем аналогичным путем из полученных уравнений исключаем x3, а именно:
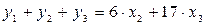 ½-26,
½-26,
 ½ 17,
½ 17,
 ,
,
 , Þ
, Þ

 Þ
Þ  ;
;
3) из второго уравнения ПФМ выразим x2, так как его нет в третьем уравнении СФМ:  .
.
Подставим полученное выражение в третье уравнение ПФМ:
 Þ
Þ  – третье уравнение СФМ.
– третье уравнение СФМ.
Таким образом, СФМ примет вид:
 ,
,
 ,
,
 .
.
Глава 6
Временные ряды в эконометрических исследованиях
Основные понятия и определения.
Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.
Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.
Каждый уровень временного ряда формируется из трендовой (T), циклической (S) и случайной (E) компонент.
Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение – мультипликативные модели временного ряда.
Аддитивная модель имеет вид: Y=T+S+E;
мультипликативная модель: Y=T × S × E.
Построение аддитивной и мультипликативной моделей сводится к расчету значений T, S и E для каждого уровня ряда.
Построение модели включает следующие шаги:
1) выравнивание исходного ряда методом скользящей средней;
2) расчет значений сезонной компоненты S;
3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной (T+E) или в мультипликативной(T × E) модели;
4) аналитическое выравнивание уровней (T+E) или (T × E) и расчет значений T с использованием полученного уравнения тренда;
5) расчет полученных по модели значений (T+S) или (T × S);
6) расчет абсолютных и/или относительных ошибок.
Автокорреляция уровней ряда – это корреляционная зависимость между последовательными уровнями временного ряда:
 , где
, где  ;
;  – коэффициент автокорреляции уровней ряда первого порядка;
– коэффициент автокорреляции уровней ряда первого порядка;
 , где
, где  ;
;  – коэффициент автокорреляции уровней ряда второго порядка.
– коэффициент автокорреляции уровней ряда второго порядка.
Формулы для расчета коэффициентов автокорреляции старших порядков легко получить из формулы линейного коэффициента корреляции.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:
· линейная  ;
;
· гипербола  ;
;
· экспонента  ;
;
· степенная функция 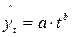 ;
;
· парабола второго и более высоких порядков 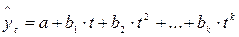 .
.
Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время t=1,2,…,n, а в качестве зависимой переменной – фактические уровни временного ряда yt. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации 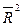 .
.
При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.
Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например  и
и  , и расчет отклонений от трендов:
, и расчет отклонений от трендов: 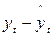 и
и  . Для дальнейшего анализа используются не исходные данные, а отклонения от тренда.
. Для дальнейшего анализа используются не исходные данные, а отклонения от тренда.
Метод последовательных разностей заключается в следующем: если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями  ; если параболический тренд – вторыми разностями
; если параболический тренд – вторыми разностями 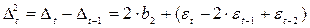 .
.
В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.
Модель, включающая фактор времени, имеет вид  . Параметры a и b этой модели определяются обычным МНК.
. Параметры a и b этой модели определяются обычным МНК.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков 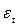 за текущий и предыдущие моменты времени.
за текущий и предыдущие моменты времени.
Для определения автокорреляции остатков используют критерий Дарбина – Уотсона и расчет величины:  0£d£4.
0£d£4.
Коэффициент автокорреляции остатков первого порядка определяется по формуле: 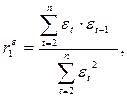 -1£
-1£  1.
1.
Критерий Дарбина – Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением  .
.
Эконометрические модели, содержащие не только текущие, но и лаговые значения факторных переменных, называются моделями с распределенным лагом.
Модель с распределенным лагом в предложении, что максимальная величина лага конечна, имеет вид  .
.
Коэффициент регрессии b0 при переменной xt характеризует среднее абсолютное изменение yt при изменении xt на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора x. Этот коэффициент называют краткосрочным мультипликатором.
В момент (t+1) воздействие факторной переменной xt на результат yt составит (b0 + b1)условных единиц; в момент времени (t+2) воздействие можно охарактеризовать суммой (b0 + b1 + b2) и т.д. Эти суммы называют промежуточными мультипликаторами. Для максимального лага (t+l) воздействие фактора на результат описывается суммой (b0 + b1 +…+ bt=b), которая называется долгосрочным мультипликатором.
Величины  ,
,  , называются относительными коэффициентами модели с распределенным лагом. Если все коэффициенты bj имеют одинаковые знаки, то для любого j 0<bj<1 и
, называются относительными коэффициентами модели с распределенным лагом. Если все коэффициенты bj имеют одинаковые знаки, то для любого j 0<bj<1 и  .
.
Величина среднего лага модели множественной регрессии определяется по формуле средней арифметической взвешенной  и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент t.
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент t.
Медианный лаг – это период, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат:
 ,
,
где 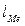 – медианный лаг.
– медианный лаг.
Оценку параметров моделей с распределенными лагами можно проводить согласно одному из двух методов: методу Койка или методу Алмон.
В распределении Койка делается предположение, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:  , где l = 0,1,2,…, 0<l<1.
, где l = 0,1,2,…, 0<l<1.
Уравнение регрессии преобразуется к виду
 .
.
После несложных преобразований получаем уравнение, оценки параметров исходного уравнения.
В методе Алмон предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному распределению:
 .
.
Уравнение регрессии примет вид  ,
,
где 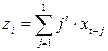 , i = 1,…, k; j = 1,…, p.
, i = 1,…, k; j = 1,…, p.
Расчет параметров модели с распределенным лагом методом Алмон проводится по следующей схеме:
1) устанавливается максимальная величина лага l;
2) определяется степень полинома k, описывающего структуру лага;
3) рассчитываются значения переменных z0,..,zk;
4) определяются параметры уравнения линейной регрессии yt от zi;
5) рассчитываются параметры исходной модели с распределенным лагом.
Модели, содержащие в качестве факторов лаговые значения зависимой переменной, называют моделями авторегрессии, например:
 .
.
Как и в модели с распределенным лагом, b0 в этой модели характеризует краткосрочное изменение yt под воздействием изменения xt на 1 ед. Долгосрочный мультипликатор в модели авторегрессии рассчитывается как сумма краткосрочного и промежуточных мультипликаторов:
 .
.
Такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.
Дата публикования: 2014-10-19; Прочитано: 5948 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
