Теоретические положения. 1. Кинематическое исследование

1. Кинематическое исследование.

Модуль цилиндрических прямозубых колес (изготовлены безсмещения инструмента) определяется по формуле

(1)

где d_a – диаметр вершин зубьев колеса (или шестерни), мм;

z – число зубьев колеса (или шестерни).

Передаточное отношение планетарного редуктора определяется по формуле Виллиса

(2)

где – передаточное отношение от центрального колеса z ₁ к водилу Н при неподвижном колесе z ₂;

– передаточное отношение от центрального колеса z ₁ к неподвижному колесу z ₂при остановленном водиле Н:

2. Определение КПД редуктора.

Потери энергии в зубчатых передачах в основном складывают­ся из потерь:

– на трение в зацеплении;

– на разбрызгивание масла;

– в подшипниках.

В данном случае потерь на разбрызгивание масла нет, так как редуктор – открытый, без смазки.

Определение КПД редуктора основано на одновременном и независимом измерении крутящих моментов на входном T ₁ и выходном T ₂ валах редуктора.

Общий КПД редуктора определяется по формуле

где Т ₁ – крутящий момент на валу электродвигателя, Нмм;

Т ₂ – крутящий (тормозной) момент на выходном валу редуктора, Нмм;

– передаточное отношение редуктора.

Крутящие моменты Т ₁ и Т ₂ определяются по формулам:

;

,

где k ₁ и k ₂– показания индикаторов.

Теоретически КПД планетарного редуктора можно определить рассмотрев соотношение мощностей на входном и выходном валах:

(3)

где Т ₁ и Т ₂ – моменты на соответствующих звеньях;

– КПД планетарной передачи.

Разделим обе части уравнения на , получим

Если всем звеньям планетарной передачи придать вращение вокруг общей оси с угловой скоростью – (т.е. применить метод инверсии), то водило остановится и мы получим зубчатую передачу с неподвижными осями. Тогда зубчатые колеса будут вра­щаться с угловыми скоростями

; ,

а уравнение мощностей этой передачи запишется

, (4)

где – реактивный момент на колесе 2;

– КПД зубчатой передачи.

Разделив обе части уравнений на и обозначив переда­точное отношение зубчатой передачи через получим

.

Уравнение равновесия всех внешних моментов имеет вид

.

Подставляя в это уравнение

,

получим

откуда

где – КПД зацеплений колес 1 и 3, 4 и 2 в предпо­ложении неподвижности водила Н. Для внешнего зацепления можно принять

.

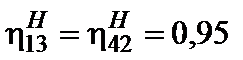Изложенный метод расчета КПД планетарных передач не учитывает потерь на трение во вращательной кинематической паре водила, коэффициент потерь в которой обычно сравнительно мал (2…3 %).