Последовательность проектировочного расчета конической зубчатой передачи

Последовательность расчета закрытой передачи.

1. Определить передаточное число 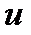и углы делительных конусов шес­терни и колеса и .

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и значения твердости рабочих по­верхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую дол­говечность , коэффициенты режима, допускаемые контактные напряже­ния и допускаемые напряжения изгиба.

4. Выбрать коэффициент длины зуба.

5. Определить средний делительный диаметр из условия контактной прочности [формула (32)].

6. Задать число зубьев шестерни , определить число зубьев колеса

7.Рассчитать внешний модуль ,и округлить его до стандартного зна­чения (см. табл. 3), а также средний модуль .

8. Определить числа зубьев эквивалентных колес и и по табл. 8 — коэффициенты формы зуба шестерни и колеса .

9. Проверить прочность зубьев по напряжениям изгиба. При неудовле­творительных результатах 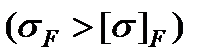необходимо путем соответствующего изменения числа зубьев и модуля при том же конусном расстоянии до­биться определенного изменения напряжений изгиба, не нарушая при этом условия контактной прочности.

10. Произвести геометрический расчет передачи (см. табл. 17).

11. Определить окружную скорость колес и по табл. 14 назначить со­ответствующую степень точности.

Последовательность расчета открытых конических передач.

1. Определить передаточное число и углы делительных конусов шестерни и колеса и .

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и значения твердости рабочих по­верхностей зубьев.

3. Определить базовое число циклов ,расчетную циклическую дол­говечность, коэффициенты режима и определить допускаемые напряжения изгиба.

4. Задать число зубьев шестерни и по передаточному числу опреде­лить число зубьев колеса .

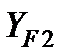5. Определить число зубьев эквивалентных колес и коэффициен­ты формы зуба и по табл. 8.

6. Выбрать коэффициент длины зуба (ширины венца) .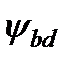

7.Из условия прочности на изгиб (формула 29) определить средний модуль , после чего подсчитать внешний модуль , значение которого округлить до ближайшего большего стандартного (см. табл. 3). При необ­ходимости следует пересчитать в зависимости от стандартного .

8. Произвести геометрический расчет передачи (см. табл. 17).

9. Определить окружную скорость колес и по табл. 14 назначить со­ответствующую степень точности зацепления.

Зубчатые передачи с зацеплением Новикова. Устройство, основные геометрические соотношения

Основной недостаток зубчатых передач с эвольвентным профилем (цилиндрических, конических, планетарных, волновых) – высокие контактные напряжения в зубьях. Они велики потому, что контактируют два зуба с выпуклыми профилями. При этом площадка контакта очень мала, а контактные напряжения соответственно высоки. Это обстоятельство сильно ограничивает "несущую способность" передач, т.е. не позволяет передавать большие вращающие моменты.

Решая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л.Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса.

Передачи с зацеплением Новикова состоят из двух цилиндрических косозубых колес (рис. 57, а) или конических колес (рис. 57, б) с винто­выми зубьями и служат для передачи момента между валами с параллель­ными или пересекающимися осями. Особенность зацепления Новикова состоит в том, что в этом зацеплении первоначальный линейный контакт (рис. 57, в) заменен точечным, превращающимся под нагрузкой в контакт с хорошим прилеганием (рис.57, г). Простейшими профилями зубьев, обес­печивающими такой контакт, являются профили, очерченные по дуге окруж­ности или близкой к ней кривой.

б)

в)

Рис. 57. Передача с зацеплением М. Л. Новикова. А - площадка контакта

Обычно профиль зубьев шестерни делается выпуклым, а профиль зубь­ев колес вогнутым или наоборот (рис.58, а, б), но могут быть передачи и с профилем зубьев шестерни и колеса, показанным на рис.58, в. Выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4-1,8 раза большие вращающие моменты.

a) б) в)

Рис. 58. Профили зубьев в передачах с зацеплением М. Л. Новикова

В зацеп­лении Новикова контакт зубьев теоретически осуществляется в точке, в эвольвентном зацеплении соприкосновение зубьев происходит по линии. Однако при одинаковых габаритных размерах передачи соприкосновение зубьев в зацеплении Новикова значительно лучше, чем соприкосновение в эвольвентном зацеплении.

К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных машин это не так важно.

Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.

В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев ( ) и дают достаточную жёсткость шестерён при их большой относительной ширине.

Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями.

Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п.

Достоинства и недостатки передач с зацеплением Новикова. Высо­кая нагрузочная способность является основным достоинством передач с зацеплением Новикова. При твердости рабочих поверхностей до НВ 350 можно принимать допускаемую нагрузку примерно в 2,5 раза больше до­пускаемой нагрузки для эвольвентных прямозубых передач тех же основ­ных размеров, выполненных из тех же материалов, с той же термической обработкой (сравнение допускаемых нагрузок произведено при коэффици­енте нагрузки К= 1).

Благодаря большей нагрузочной способности передачи с зацеплением Новикова более компактны, имеют почти в 2 раза меньшие габариты по сравнению с передачами с эвольвентным зацеплением при одинаковой пе­редаваемой мощности.

Передачи с зацеплением Новикова допускают большее передаточное число, а вследствие хорошо удерживающейся масляной пленки между со­прикасающимися зубьями уменьшается изнашивание зубьев, повышается КПД передачи.

Потери на трение в зацеплении Новикова примерно в 2 раза меньше, чем потери в эвольвентном зацеплении. Шум во время их работы значи­тельно ниже.

Недостатками являются:

- большая (чем в эвольвентных зацеплениях) чувствительность к изме­нению межосевого расстояния;

- с увеличением нагрузки в зацеплении возрастает осевая составляю­щая, что, в свою очередь, усложняет конструкцию применяемых подшипниковых узлов;

- при ухудшении контакта (например, в случае перекоса валов и изме­нения межосевого расстояния) вся нагрузка, действующая на зубья, может сосредоточиться на небольшом участке длины зубьев, в ре­зультате чего зубья могут оказаться сильно перегруженными;

- необходимость иметь две специальные фрезы для нарезания зубьев (для шестерни и колеса).

Стандартные исходные контуры для цилиндрической зубчатой пере­дачи с зацеплением Новикова для выпуклых (шестерня) и вогнутых (колесо) зубьев (рис. 59, а).

Основные геометрические размеры этих передач (рис. 59, б) опреде­ляют в зависимости от значения нормального модуля т_п (табл. 18 и 19).

а)

Рис. 59. Косозубая передача с зацеплением М.Л. Новикова

Таблица 18. Стандартные значения модулей для передачи с зацеплением Новикова

1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-й ряд
1,6		6,3
2,0	1,8		7,1
2,5	2,25			31,5	35,5
3,15	2,8	12,5	П,2
	3,55
	4,5
	5,6		22,4

Таблица 19. Геометрические параметры передачи с зацеплением Новикова

Параметр, обозначение	Расчетные формулы
Нормальный модуль
Торцовый модуль
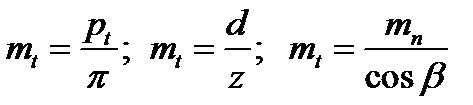
Диаметр вершин зубьев
Делительный диаметр
Основной диаметр
Диаметр впадин зубьев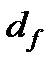
Нормальный шаг
Торцовый шаг
Осевой шаг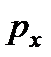
Окружная толщина зубьев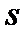
Окружная ширина впадин зубьев
Высота зуба
Высота головки зуба
Высота головки зуба
Радиальный зазор с
Ширина венца b
Межосевое расстояние

Примечание. — угол наклона зубьев; ; — целое число осевых шагов р_х в ширине венца; — часть ширины венца больше целого числа осевых шагов (ширину венца рекомендуется выбирать с учетом выполнения условия ); — суммарное число зубьев.