Скорость распространения волн на поверхности потока

Применим такую схему расчета, которая позволяла бы рассматривать установившееся движение. Имея в виду, что положение волны меняется, представим возмущение на поверхности потока движущегося с такой скоростью, чтобы она была равна скорости распространения волны.

Представим одиночную волну малой высоты 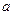, перемещающуюся по свободной поверхности со скоростью 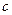в плоском потоке глубиной 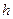. Малая высота волны в данном случае означает, что ее высота значительно меньше ее длины, т.е. 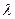>> 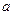. Поток жидкости движется с такой же скоростью, что и волна, но в противоположном направлении; тогда процесс распространения волны можно рассматривать как стационарный. Площадь живого сечения в сечении 2, рис. 10.3 несколько увеличивается, что приводит к незначительному уменьшению скорости течения до значения 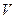< 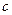. Не учитывая потерь энергии и принимая распределение скоростей по сечению равномерным, применим уравнение Бернулли к сечениям 1 и 2, рис. 10.3:

. (10.2)

Уравнение неразрывности для потока единичной ширины

, откуда . (10.3)

Подставляя значение 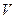из (10.3) в (10.2) и решая полученное уравнение относительно 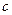, получаем

. (10.4)

Раскрываем под корнем скобку и не принимаем во внимание , так как 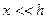; в результате получаем

. (10.5)

Дробь под корнем тождественно преобразуем, умножая числитель и знаменатель на 2

.

Подставляя последнее выражение в (10.5) и не учитывая в знаменателе величину , получим

. (10.6)

Для того, чтобы избавиться от корня, применим формулу приближенного вычисления при малом

. (10.7) В результате (10.6) перейдёт в формулу Сен-Венана

,

а при очень малой высоте волны в формулу Лагранжа

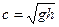. (10.8)

В канале с наклоном дна к горизонту под углом

. (10.9)