Общий случай

Рассмотрим неравномерное плавноизменяющееся движение воды в открытом канале, рис. 6.3.Применим уравнение Бернулли к двум сечениям потока 1 и 2, находящихся на бесконечно малом расстоянии dl друг от друга. Отметка дна в первом сечении z, глубина h, средняя скорость V, а во втором сечении соответственно z+dz, h+dh, V+dV (приращения отметки дна, глубины и скорости могут быть и положительными и отрицательными). С учетом введенных обозначений уравнения Бернулли принимает вид

Рис. 6.3.

,

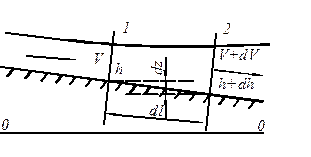
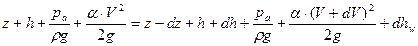(6.1)

где 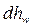- потери энергии по длине между расчетными сечениями.

Не учитывая величину второго порядка малости 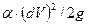, после преобразований имеем из (6.1)

,

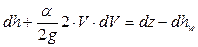(6.2)

Принимая во внимание, что

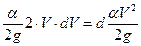и ,

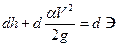разделив обе части уравнения (6.2) на dl, получим

,

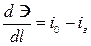(6.3)

где 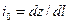- уклон дна русла, 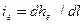- гидравлический уклон.

Уравнение (6.3) является основным дифференциальным уравнением установившегося неравномерного движения в открытом русле.

При определении гидравлического уклона 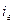в данном случае делается допущение, что потери при неравномерном плавноизменяющемся движении выражаются той же зависимостью, что и при равномерном движении, т.е.

.

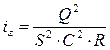(6.4)

Если при равномерном движении величина 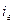постоянна по длине потока, то при неравномерном по причине изменения глубины h, площади сечения S, значений C и R величина 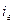также изменяется вдоль потока.

Уравнение (6.3) преобразуем так (умножив и разделив правую часть на dh)

,

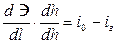или

.

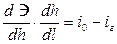Окончательно

.

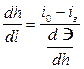(6.5)