Основы методики математического моделирования

Учебные элементы:

1. Модель состава системы.

2. Модель структуры системы.

3. Модели типа чёрный и белый ящик.

Как уже отмечалось выше, существует два метода (способа) получения математической модели: аналитический и эмпирический. Каждый из них имеет свой алгоритм и особенности.

Процесс построения аналитической математической модели и её использования для изучения объекта состоит из следующих этапов:

1. Изучение конструкции объекта и процессов протекающих в нём.

2. Составление структурной схемы, разделение на составные части (декомпозиция).

3. Введение допущений и упрощений.

4. Составление математических зависимостей.

5. Выбор метода решения математических зависимостей.

6. Решение математических зависимостей (как правило, с помощью ЭВМ).

7. Анализ полученных данных.

Первые три этапа не формализованы и в каждом случае носят индивидуальный характер. Полное математическое описание системы представляет собой совокупность уравнений сохранения, уравнение состояния и условий однозначности.

В общем случае для каждого элемента записываются:

1) уравнение сохранения массы;

2) уравнение сохранения энергии;

3) уравнение сохранения количества движения;

4) уравнение состояния.

Условия однозначности — это геометрические, физические и краевые характеристики системы.

Различают два вида краевых условий:

Начальные и граничные, которые определяют единственность решения.

Начальные условия — это значение параметров в начальный момент времени.

Краевые условия — сведение о значении параметров на границе системы.

На границе рассматриваемой области граничные условия можно задать несколькими способами:

а) в виде значений искомой функции;

б) в виде значений производной искомой функции по пространственным координатам;

в) в виде уравнение баланса потоков.

В случаях а-в говорят о граничных условиях первого, второго, третьего рода.

Укрупнённый алгоритм аналитического математического моделирования показан на рис. 1.9.

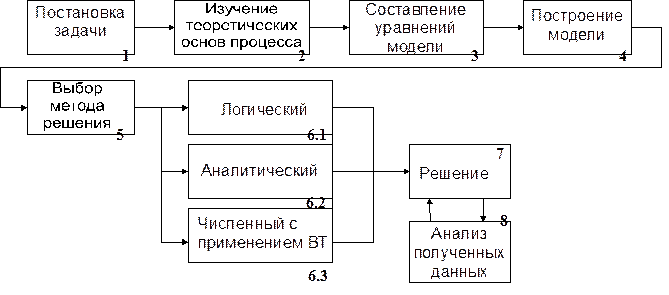
Рис. 1.9 Этапы получения и применения аналитической математической модели

Таким образом, аналитические модели позволяют построить модели состава и модели структуры системы.

Модель состава ограничивается снизу тем, что считается элементом, а сверху границей системы. Как эта граница, так и границы разбиения на подсистемы определяются целями построения модели и, следовательно, не имеют абсолютного характера, поэтому существует многообразие моделей состава системы.

Модель структуры описывает существенные связи между элементами (компонентами модели состава).

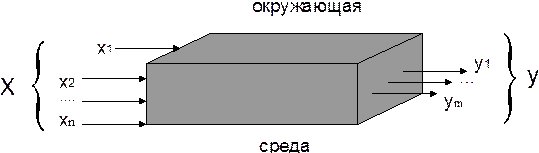
Эмпирический метод построения математической модели основывается на понятии “ чёрный ящик ”, введённое У. Р. Эшби. “Чёрным ящиком” называют систему, внутреннее содержание которой наблюдателю неизвестно, а доступными ему являются только входы и выходы системы (1.10).

Рис. 1.10 Модель “чёрного ящика”

Эта на первый взгляд простая модель отражает два важных свойства системы: целостность и обособленность от среды.

Представление такой модели осуществляется несколькими способами.

Во многих случаях достаточно содержательного словесного описания входов и выходов; тогда модель “чёрного ящика” является просто их списком.

В других случаях строят количественное описание некоторых или всех входов и выходов. В этом случае тем или иным способом задаются два множества X и Y, например, путём наблюдения за входами и выходами.

Простота модели “чёрного ящика” обманчива, потому что построение такой модели не является тривиальной задачей, так как на вопрос о том, сколько и какие именно входы и выходы следует включать в модель не всегда однозначны.

Главной причиной множественности входов и выходов в модели “чёрного ящика”, является то, что всякая реальная система, как и любой объект, взаимодействует с объектами окружающей среды неограниченным числом способов. При построении модели из бесчисленного множества входов, выходов, связей отбирается их конечное число. Критерием отбора при этом является целевое назначение модели, существенность той или иной связи по отношению к этой цели.

Именно здесь возможны ошибки. Тот факт, что из рассмотрения исключаются остальные связи, не лишает их реальности, и они всё равно действуют.

Нередко оказывается, что казавшееся несущественным или неизвестным при построении модели, на самом деле является важным и должно быть учтено.

Особое значение это имеет при задании цели системы, т.е. при определении её выходов. Это относится к описанию существующей системы по результатам её обследования, и к проекту пока ещё не существующеё системы.

Для решения этого противоречия главную цель сопровождают заданием дополнительных целей.

Важно подчеркнуть, что выполнение только основной цели не достаточно, что невыполнение дополнительных целей может сделать ненужным или даже вредным и опасным достижение основной цели. Этот момент заслуживает особого внимания, так как на практике часто обнаруживается незнание, непонимание или недооценка важности указанного положения.

Между тем оно является одним из центральных во всей системологии.

Модель “чёрного ящика” часто называется в ряде случаев единственно применимой при изучении систем в силу объективной невозможности попасть внутрь системы (исследование психики человека) без нарушения её целостности или при действительном отсутствии данных о внутреннем устройстве системы. Например, мы не знаем как “устроен электрон”, но известно, как он взаимодействует с электрическим и магнитными полями, с гравитационным полем. Это и есть описание электрона на уровне модели “чёрного ящика”.

Таким образом, при всём многообразии реальных систем принципиально различных типов моделей, очень немного: модель типа “чёрного ящика”, модель состава, модель структуры, а также их разумное сочетание и, прежде всего объединение всех трёх моделей, т.е. структурная схема системы (рис. 1.11).

Рис. 1.11 Типы моделей

Можно сказать, что структурная схема “белый ящик” получается как результат “суммирования” всех трёх типов моделей. Все указанные типы моделей являются формальными, относящимися к любым системам и, следовательно, не относящимися ни к одной конкретной системе. Чтобы получить модель определённой технической системы, нужно придать модели конкретное содержание. Процесс построения содержательных моделей является процессом интеллектуальным, творческим.

Вопросы:

1. Сколько этапов содержит процедура получения модели?

2. Что представляет собой полное математическое описание системы?

3. Как интерпретируются условия однозначности?

4. Чем отличаются начальные условия от граничных условий?

5. Чем отличается модель состава от модели структуры?

6. Почему приходится пользоваться моделью чёрный ящик? Какова его сущность?

Раздел 1

Тема 2 Математическое моделирование

Основные понятия математического моделирования

Учебные элементы:

1. Математическая модель

2. математическое моделирование

3. параметр

4. фазовая переменная

5. параметрическая схема

6. требования к качеству математической модели

Математическая модель (ММ) -это множество математических объектов (чисел, переменных, матриц, множеств, точек, отрезков переменных и т. д.), связанных определенным образом. Такая модель отражает некоторые свойства моделируемого объекта, интересующие пользователя.

Создание ММ и оперирование с ней для получения полезной информации об объекте называют математическим моделированием.

Среди свойств объекта, отражаемых ММ, различают свойства систем, элементов систем и внешней среды, в которой должен функционировать объект. Свойство – это существенный признак объекта, определяемый количественно, например, геометрические размеры, масса.

Количественное выражение свойств осуществляется с помощью величин, называемых параметрами. Различают выходные, внутренние и внешние (входные) параметры (рис. 1.7).

	Q

X Y

Рис. 1.7 Параметрическая схема объекта моделирования

Если их число соответственно m, n, b, а векторы этих параметров:

Y = (y₁, y₂, …, y_m); Q = (q₁, q₂, …, q_n); X = (x₁, x₂, …, x_b), то

ММ можно отразить отношением в виде математической функции:

Y = F (X, Q) (1.1)

Модель может отражать состояние объекта. Состояние – это совокупность значений свойств объекта (параметров) в определенный момент времени.

Величины, характеризующие физическое или информационное состояние моделируемого объекта называют фазовыми переменными — V. Их изменение во времени называют переходным процессом. Тогда ММ представляется в форме:

LV = j (z) (1.2)

Здесь L — некоторый оператор; z — вектор независимых переменных, в общем случае включающий время и пространственные координаты;

j (z) — заданная функция независимых переменных.

К математическим моделям предъявляются требования универсальности, адекватности, точности и экономичности.

Степень универсальности ММ характеризует полноту отображения в модели свойств реального объекта. Математическая модель отражает лишь некоторые свойства объекта. Большинство моделей предназначено для отображения физических или информационных процессов, при этом не требуется, чтобы ММ описывала такие свойства как геометрическая форма объекта.

Например, ММ резистора в виде уравнения закона Ома, характеризует свойства резистора пропускать электрический ток, но не отображает габариты резистора, его цвет, стоимость и т.д.

Точность ММ оценивается степенью совпадений параметров реального объекта и значений тех же параметров, рассчитанных с помощью оцениваемой ММ.

Если отражаемые в ММ свойства оцениваются вектором выходных параметров: Y = (y₁, y₂, …, y_m), тоотносительная погрешность e_j расчёта параметра определяется как:

e_j =(y_{j м} - y_{j ист})/ y_{j ист}

где: y_{j м} — модельное значение j параметра; y_{j ист.}— истинное значение.

Полученная векторная оценка: e = (e₁, e₂, …, e_m) при необходимости может быть сведена к скалярной, путём использования какой-либо нормы вектора e, например:

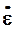_М = ккe кк= max e_j, j є [1: m] (1.3)

Адекватность ММ — способность отображать заданные свойства объекта с погрешностью не выше заданной. Как правило, адекватность модели имеет место лишь в ограниченной области изменения параметров — области адекватности (ОА) математической модели:

ОА = {X кe_M Ј d} (1.4)

Где: d> 0 — заданная константа, равная предельно допустимой погрешности модели.

Экономичность ММ характеризуется затратами ресурсов, в том числе и вычислительных (затраты машинного времени и памяти).

Требования высоких точностей, степени универсальности, широкой области адекватности, с одной стороны и высокой экономичности с другой, противоречивы.

Наилучшее компромиссное удовлетворение этих противоречивых требований зависит от особенностей решаемых задач, что в совокупности с большим разнообразием объектов обусловливает широкий спектр математических моделей.

Вопросы:

Что понимают под терминами "математическая модель” и "математическое моделирование”?

Как отражаются количественно свойства объекта в модели?

Чем характеризуются свойства моделируемого объекта?

Какие требования предъявляются к ММ?