Теорема (о модуле векторного произведения )

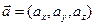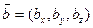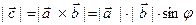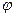Модуль векторного произведения двух векторов и может вычисляться по формуле , где есть угол между векторами и . Если векторы , не являются коллинеарными, то модуль векторного произведения равен площади параллелограмма, построенного на векторах и .

Доказательство. Если векторы 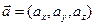, 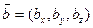являются коллинеарными, то их векторное произведение равно нулевому вектору, а модуль нулевого вектора равен нулю. Так как угол между коллинеарными векторами равен 0 или 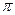, то .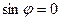

Таким образом, доказываемая формула справедлива для коллинеарных векторов.

Пусть векторы и не являются коллинеарными.

Обозначим направляющие косинусы вектора как 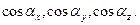Так как, по определению, направляющие косинусы есть компоненты орта вектора , то для них справедлива формула 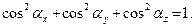Компоненты вектора выражаются через модуль вектора и направляющие косинусы по формулам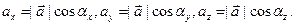

Аналогично, обозначим направляющие косинусы вектора как 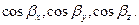Для них также справедлива формула 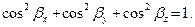Кроме того, выполняются равенства для компонент вектора в виде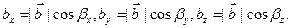

Косинус угла 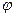между векторами и вычисляется как скалярное произведение между их ортами по формуле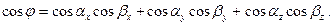

Найдем далее квадрат модуля векторного произведения:

.

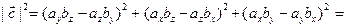
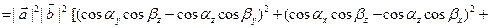
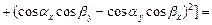
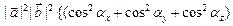
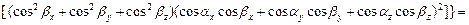
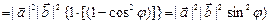Отсюда следует 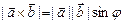, что и завершает доказательство первой части теоремы.

Если векторы , не являются коллинеарными, то на них можно построить параллелограмм. Площадь любого параллелограмм вычисляется как произведение длины основания параллелограмма на его высоту. В нашем случае длина основания равна 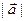, а высота равна 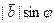. Таким образом, теорема полностью доказана.

Определение. Векторно-скалярным или смешанным произведением трех упорядоченных векторов 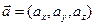, , 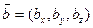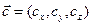в реальном пространстве называют число, найденное по правилу 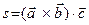, где для первых двух векторов составляется векторное произведение, которое затем скалярно умножается на третий вектор.

Учитывая определения векторного и скалярного произведений, значение смешанного произведения вычисляют по формуле

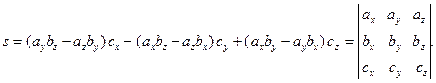
Если векторы 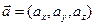, , 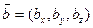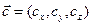являются компланарными, то один из векторов, может быть представлен в виде линейной комбинации двух других. В этом случае одна из строк определителя смешанного произведения будет линейной комбинацией двух других строк. Как известно, значение такого определителя равно нулю.

Таким образом, смешанное произведение трех компланарных (лежащих в одной плоскости) векторов равно нулю.

Рассмотрим далее скалярное произведение вектора 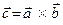на вектор 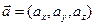. По определению смешанного произведения, мы получим определитель с двумя одинаковыми строками, который равен нулю. Это означает, что векторное произведение 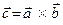ортогонально (перпендикулярно) одному из перемножаемых векторов. Аналогично, показывается, что векторное произведение перпендикулярно и второму из перемножаемых векторов. Таким образом, можно утверждать, что векторное произведение всегда дает вектор, который перпендикулярен обоим векторам-сомножителям.

Основное алгебраическое свойство смешанного произведения состоит в том, что циклическая перестановка векторов, не меняет его величины, т.е.

,

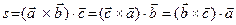что проверяется непосредственно по определяющей формуле.

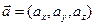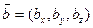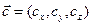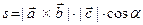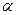Рассмотрим параллелепипед, построенный на векторах , , и перепишем векторно-скалярное произведение в виде , где есть угол между векторам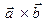и и 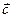. Ранее было показано, что модуль векторного произведения 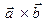равен площади параллелограмма, построенного на векторах 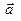и 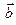. Величина 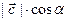по определению равна проекции вектора 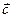на вектор 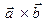, а модуль этой величины равен длине высоты параллелепипеда. Отсюда, окончательно, получаем, что модуль смешанного произведения равен объему исходного параллелепипеда.

Определение. Упорядоченная тройка некомпланарных геометрических векторов 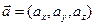, , 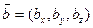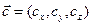называется правой, если величина смешанного произведения строго положительна. Если же величина смешанного произведения строго отрицательна, то указанная тройка векторов называется левой.

Вычислим смешанное произведение для векторов канонического базиса 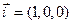, , 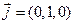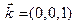. По определяющей формуле

.

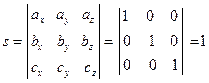Таким образом, векторы канонического базиса образуют правую тройку, а, соответствующую этим векторам систему координат 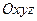, называют правой прямоугольной системой координат. На рисунках ось 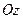обычно направляют вверх, а ос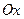и и 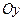располагают таким образом, чтобы наблюдателю, находящемуся внутри телесного угла, образованного тремя осями, кратчайшие повороты от 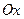оси к оси 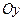и от о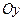си к оси 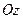казались происходящими против часовой стрелки.

Покажем, что векторы 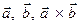образуют правую тройку, если векторы 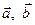являются неколлинеарными. Их смешанное произведение равно скалярному произведению вектора 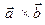на себя. Так как векторы 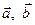являются неколлинеарными, то из доказанного выше следствия следует, что вектор 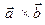отличен от нулевого вектора. Отсюда и аксиом скалярного произведения следует, что 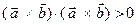, так что векторы 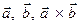образуют правую тройку.

Таким образом, показано, что векторное произведение 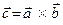удовлетворяет следующим трем условиям:

1) длина вектора 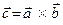равна площади параллелограмма, построенного на векторах 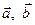, и может вычисляться по формуле ;

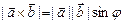2) вектор 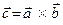перпендикулярен и вектору и вектору ;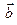

3) упорядоченная тройка векторов 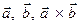является правой.