 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные пространства геометрических векторов на плоскости и реальном пространстве строятся, соответственно, на основе евклидовых пространств арифметических векторов и
|
|
Определение. Любая упорядоченная пара точек 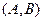 называется направленным отрезком и обозначается как
называется направленным отрезком и обозначается как 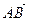 .
.
Первый элемент пары – точку 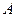 называют началом или точкой приложения направленного отрезка. Второй элемент пары – точку
называют началом или точкой приложения направленного отрезка. Второй элемент пары – точку 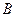 называют окончанием направленного отрезка. Изображается направленный отрезок в виде стрелочки с началом в точке
называют окончанием направленного отрезка. Изображается направленный отрезок в виде стрелочки с началом в точке 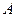 и окончанием в точке
и окончанием в точке 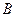 .
.
Будем говорить, что любые два направленных отрезка 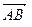 и
и 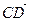 имеют одинаковую длину и направление, если равны арифметические векторы
имеют одинаковую длину и направление, если равны арифметические векторы 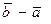 и
и 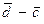 .
.
Определение. Геометрическим вектором 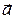 называется множество всех направленных отрезков, имеющих одинаковую длину и направление.
называется множество всех направленных отрезков, имеющих одинаковую длину и направление.
О всяком направленном отрезке 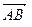 из этого множества говорят, что он представляет геометрический вектор
из этого множества говорят, что он представляет геометрический вектор  (получен приложением вектора
(получен приложением вектора  к точке
к точке 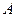 ). Каждому геометрическому вектору однозначно соответствует некоторый арифметический вектор, равный разностям компонент окончания и начала любого направленного отрезка, представляющего данный геометрический вектор.
). Каждому геометрическому вектору однозначно соответствует некоторый арифметический вектор, равный разностям компонент окончания и начала любого направленного отрезка, представляющего данный геометрический вектор.
Для любого арифметического вектора 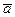 существует единственный направленный отрезок
существует единственный направленный отрезок 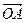 , который называют радиус - вектором точки
, который называют радиус - вектором точки 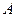 и обозначают
и обозначают 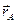 . Все направленные отрезки, имеющие одинаковую длину и направление с радиус – вектором
. Все направленные отрезки, имеющие одинаковую длину и направление с радиус – вектором 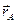 образуют геометрический вектор
образуют геометрический вектор  . Таким образом, каждому арифметическому вектору
. Таким образом, каждому арифметическому вектору 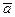 соответствует единственный геометрический вектор
соответствует единственный геометрический вектор  , длина и направление которого задается этим арифметическим вектором.
, длина и направление которого задается этим арифметическим вектором.
Обратно, каждому геометрическому вектору  соответствует единственный арифметический вектор
соответствует единственный арифметический вектор 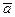 , который определяет длину и направление любого направленного отрезка, составляющего этот геометрический вектор.
, который определяет длину и направление любого направленного отрезка, составляющего этот геометрический вектор.
Иногда используют выражение «задан вектор  ». Это означает, что задан геометрический вектор, который полностью определяется арифметическим вектором
». Это означает, что задан геометрический вектор, который полностью определяется арифметическим вектором 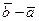 . Радиус – вектор этого геометрического вектора равен
. Радиус – вектор этого геометрического вектора равен 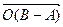 , а любой направленный отрезок этого геометрического вектора с началом в произвольной точке
, а любой направленный отрезок этого геометрического вектора с началом в произвольной точке 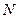 равен
равен 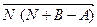 .
.
Геометрические векторы  и
и  называются равными
называются равными 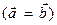 , если множества представляющих их направленных отрезков совпадают. Два любых геометрических вектора равны тогда и только тогда, когда равны соответствующие им арифметические векторы. Как обычно, равенство понимается в том смысле, что слева и справа от знака равенства стоит один и тот же элемент, только записанный в различных формах.
, если множества представляющих их направленных отрезков совпадают. Два любых геометрических вектора равны тогда и только тогда, когда равны соответствующие им арифметические векторы. Как обычно, равенство понимается в том смысле, что слева и справа от знака равенства стоит один и тот же элемент, только записанный в различных формах.
Суммой 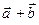 двух любых геометрических векторов
двух любых геометрических векторов  и
и  называется геометрический вектор
называется геометрический вектор 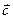 , которому соответствует арифметический вектор
, которому соответствует арифметический вектор 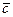 с компонентами
с компонентами  .
.
Если геометрические векторы  и
и  представлены направленными отрезками
представлены направленными отрезками 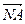 и
и 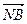 , имеющими общее начало
, имеющими общее начало 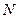 , то их сумма представлена направленным отрезком
, то их сумма представлена направленным отрезком 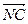 . Этот направленный отрезок приложен к точке
. Этот направленный отрезок приложен к точке 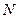 и имеет окончание в точке с координатами
и имеет окончание в точке с координатами 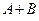 . На рисунке направленный отрезок
. На рисунке направленный отрезок 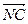 изображается как диагональ параллелограмма, построенного на направленных отрезках
изображается как диагональ параллелограмма, построенного на направленных отрезках 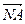 и
и 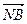 . Сложение геометрических векторов по указанной схеме называют правилом параллелограмма.
. Сложение геометрических векторов по указанной схеме называют правилом параллелограмма.
Если геометрические векторы  и
и  представлены направленными отрезками
представлены направленными отрезками 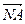 и
и 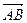 , то их сумма представлена направленным отрезком
, то их сумма представлена направленным отрезком 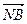 . На рисунке направленный отрезок
. На рисунке направленный отрезок 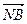 изображается как стрелочка, идущая в треугольнике
изображается как стрелочка, идущая в треугольнике 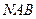 от точки
от точки  к точке
к точке 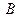 . Сложение геометрических векторов по указанной схеме называют правилом треугольника.
. Сложение геометрических векторов по указанной схеме называют правилом треугольника.
Произведением числа 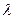 на геометрический вектор
на геометрический вектор  называется геометрический вектор
называется геометрический вектор 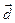 , обозначаемый
, обозначаемый 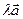 , которому соответствует арифметический вектор
, которому соответствует арифметический вектор 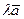 .
.
Нулевой геометрический вектор обычно обозначается как  и соответствует арифметическому вектору
и соответствует арифметическому вектору 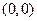 или
или  .
.
Ранее было показано, что для арифметических векторов любой размерности выполняются восемь аксиом линейного пространства. Так как основные операции для геометрических векторов введены посредством операций над двумерными и трехмерными арифметическими векторами, то для них также справедливы восемь аксиом линейного пространства. Таким образом, по построению, между геометрическими и арифметическими векторами одинаковой размерности установлено взаимно однозначное соответствие, согласованное с основными операциями вещественных линейных пространств, что позволяет считать геометрические векторы на плоскости и реальном пространстве конкретными векторами.
Как следует из общих определений, в арифметическом пространстве 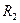 скалярное произведение для любых двух векторов
скалярное произведение для любых двух векторов 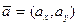 и
и 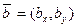 определяется по формуле
определяется по формуле  . Соответственно, в арифметическом пространстве
. Соответственно, в арифметическом пространстве  скалярное произведение для любых двух векторов
скалярное произведение для любых двух векторов  и
и 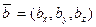 определяется по формуле
определяется по формуле 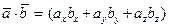 .
.
Определение. Скалярным произведением геометрических векторов  ,
,  называют скалярное произведение соответствующих арифметических векторов
называют скалярное произведение соответствующих арифметических векторов 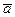 ,
, 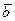 , т.е.
, т.е.  .
.
Отсюда следует, что в пространстве геометрических векторов на плоскости скалярное произведение вычисляется по формуле 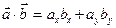 , если заданы точки
, если заданы точки 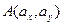 и
и 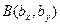 . Аналогично, в реальном пространстве
. Аналогично, в реальном пространстве 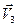 скалярное произведение вычисляется по формуле
скалярное произведение вычисляется по формуле 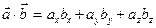 , если заданы точки
, если заданы точки 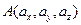 и
и 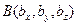 .
.
Длину (модуль) арифметического вектора определяют и вычисляют, соответственно, по формулам 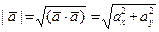 для
для 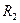 и
и  для
для  .
.
Определение. Длиной (модулем) геометрического вектора  называют длину, соответствующего ему арифметического вектора
называют длину, соответствующего ему арифметического вектора 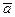 .
.
Так, если геометрический вектор  в реальном пространстве задан арифметическим вектором
в реальном пространстве задан арифметическим вектором 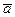 с компонентами
с компонентами 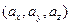 , то длина вектора
, то длина вектора  находится по формуле
находится по формуле
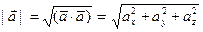 .
.
В частности, нулевой геометрический вектор  имеет нулевую длину.
имеет нулевую длину.
Если, например, геометрический вектор  представлен направляющим отрезком
представлен направляющим отрезком 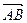 в реальном пространстве, то ему соответствует арифметический вектор
в реальном пространстве, то ему соответствует арифметический вектор 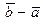 , и его длину в этом случае находят по формуле
, и его длину в этом случае находят по формуле  , где
, где  есть компоненты арифметического вектора
есть компоненты арифметического вектора 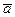 и
и  есть компоненты вектора
есть компоненты вектора 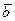 .
.
Длину направленного отрезка 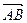 обозначают
обозначают 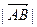 и определяют по формуле
и определяют по формуле 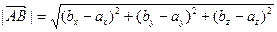 . Отметим, что длина направленного отрезка равна расстоянию
. Отметим, что длина направленного отрезка равна расстоянию 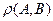 между точками
между точками 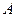 и
и 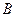 .
.
Модуль произведения числа 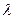 на геометрический вектор
на геометрический вектор  находится по формуле
находится по формуле  , что следует непосредственно из приведенных формул. Если число
, что следует непосредственно из приведенных формул. Если число 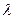 строго положительно, то вектор
строго положительно, то вектор 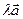 имеет то же направление, что и вектор
имеет то же направление, что и вектор  . Если число
. Если число 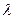 строго отрицательно, то вектор
строго отрицательно, то вектор 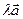 имеет то же направление, что и вектор
имеет то же направление, что и вектор 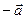 , то есть, направлен в противоположную сторону.
, то есть, направлен в противоположную сторону.
Определение. Угол между двумя любыми ненулевыми геометрическими векторами  и
и  определяется по формуле
определяется по формуле 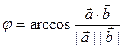 .
.
В частности, в реальном пространстве 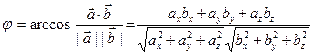 .
.
В задачах, где известен угол 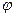 между векторами
между векторами  и
и  и длины этих векторов, скалярное произведение вычисляют по формуле
и длины этих векторов, скалярное произведение вычисляют по формуле 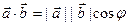 .
.
Дата публикования: 2014-11-18; Прочитано: 880 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
