 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
лекций по микроэкономике 32 страница
|
|
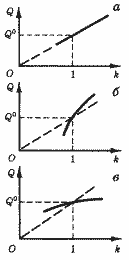
Рис. 14. Постоянная (а), возрастающая (б) и убывающая (в) отдача от масштаба
Таким образом, если предприятие хочет увеличить выпуск продукта в k раз, сохраняя пропорцию между объемами потребления ресурсов, то ему придется увеличить объем потребления каждого ресурса:
- в k раз, если отдача от масштаба постоянна;
- меньше, чем в k раз, если отдача от масштаба возрастает;
- больше, чем в k раз, если отдача от масштаба убывает.
Если масштаб производства может изменяться в широких пределах, то характер отдачи от масштаба не остается одним и тем же во всем диапазоне изменений.
Для того чтобы фирма могла функционировать, требуется некоторый минимальный уровень потребления ресурсов - постоянные затраты.
При малых объемах производства отдача от масштаба оказывается возрастающей: так как величина постоянных затрат остается неизменной, значительное увеличение выпуска продукта может быть достигнуто при относительно небольшом увеличении общих затрат ресурсов.
При больших объемах отдача от масштаба оказывается убывающей вследствие снижения предельного продукта каждого ресурса.
Помимо других обстоятельств убывающая отдача от масштаба на крупных предприятиях связана с усложнением управления производством, нарушениями координации деятельности различных производственных звеньев и т. д. Характерная кривая представлена на рис. 15. Участок слева от точки В характеризуется возрастающей отдачей от масштаба, справа - убывающей. В окрестности точки В отдача от масштаба приблизительно постоянна.
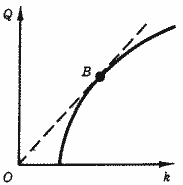
Рис. 15. Различная отдача от масштаба на различных участках кривой
РАЗДЕЛ 3. Технический прогресс и производственная функция
Как уже говорилось, производственная функция описывает техническую сторону производства. При этом все приведенные в разделах 1 и 2 соображения исходили из неизменности технического уровня производства: замена одного ресурса другим, изменение масштаба производства и т. д., - все эти изменения были переходами от одного производственного варианта к другому в пределах множества производственных возможностей, причем само это множество предполагалось неизменным; неизменной была и производственная функция. В то же время в реальной жизни фирмы происходят изменения и другого рода: изобретаются новые материалы, старое оборудование заменяется более совершенным, работники приобретают новые знания и т. д. Кроме того, может совершенствоваться и продукция. Однако такие изменения мы здесь рассматривать не будем: теория предполагает, что продукт идеально однороден, тождествен самому себе, а усовершенствованный продукт - это уже другой продукт. Мы ограничимся рассмотрением только таких изменений в производстве, которые влияют лишь на затраты ресурсов и никак не сказываются на качестве продукта. Как же производственная функция отражает такие изменения в производстве, которые характеризуются как технический прогресс? Чтобы в дальнейшем избежать неясности, вначале исключим изменения, которые не относятся к техническому прогрессу. Допустим, что мы рассматриваем производственную функцию, имеющую своими аргументами всего два фактора - труд (L) и капитал (K). Одна из изоквант такой производственной функции показана на рис. 16. Допустим, что фирма, оставаясь в пределах исходных технических возможностей, механизирует производство, увеличивая количество оборудования (т. е. Заложенного в производство капитала) и высвобождая некоторое количество труда; при этом она сохраняет прежний выпуск продукции. На рис. 16 этому изменению соответствует переход по изокванте из точки А в точку В. Можно ли такое изменение считать проявлением технического прогресса? Разумеется, нет: мы остались в пределах прежних производственных возможностей, произошло лишь замещение одного ресурса другим.
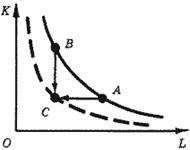
Рис. 16. Сдвиг изокванты производственной функции в результате технического прогресса
Ситуация была бы совершенно иной, если бы фирма, сохранив выпуск продукции, смогла бы уменьшить затраты труда без увеличения затрат капитала или, наоборот, смогла бы уменьшить затраты капитала без уменьшения затрат труда, т. е. смогла бы перейти из точки А или В в точку С, лежащую ниже и левее старой изокванты. В пределах исходных производственных возможностей такой переход не мог бы осуществиться: в точке С производственная функция принимала меньшее значение, чем на изокванте, проходящей через точки A и В. Значит, должна была измениться производственная функция. При этом изокванта, соответствующая исходному выпуску продукции, должна переместиться влево вниз и пройти через точку С.
Итак, технический прогресс - появление новых производственных возможностей. При этом прежние возможности не исчезают. Изобретение новых материалов не исключает использование традиционных. Так, внедрение капрона в качестве конструкционного материала в машиностроении не исключило применение стали - в каждом случае нужно выбирать более эффективный из имеющихся материалов. Получение новых знаний не означает немедленного забвения всего старого. Таким образом, технический прогресс означает расширение множества производственных возможностей - "холм", о котором шла речь в разделе 1, "обрастает дополнительным слоем" (рис. 17). При этом варианты, которые в исходном множестве были технически эффективными, становятся неэффективными, и производственная функция должна учитывать новые эффективные варианты.
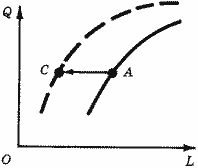
Рис. 17. Сдвиг графика производствен результате технического прогресса
Изложенная здесь точка зрения на то, как изменения производственной функции отражают технический прогресс, получила широкое распространение и развитие. На ее основе разработаны показатели интенсивности технического прогресса; изменение наклона изоквант при их сдвиге позволяет классифицировать виды технического прогресса, различая трудосберегающее, капиталосберегающее, природосберегающее направления. Однако при этом возникает вопрос: почему определенная комбинация ресурсов "до прогресса" позволяла получить максимум 100 единиц продукта, а "после прогресса" та же самая комбинация тех же самых ресурсов позволяет получить, скажем, 120 единиц продукта? Если мы учли все используемые ресурсы и ничего не упустили, какая же сила породила дополнительные 20 единиц продукта?
На этот вопрос можно дать такой ответ: количество ресурсов осталось тем же самым, но изменилось их качество, так что "после прогресса" использованы не совсем те же самые ресурсы, которые были "до".
Однако такое объяснение плохо согласуется с теми допущениями о производственной функции, которые были введены в разделе 1: одно из них сводилось к тому, что каждый аргумент производственной функции соответствует абсолютно однородному ресурсу и что, следовательно, ресурс иного качества - это иной ресурс.
Здесь мы должны вернуться к тому обстоятельству, которое вскользь было упомянуто в разделе 1: термином "производственная функция" обозначают функции по крайней мере двух разных типов. Один тип охватывает функции, которые были предметом обсуждения в двух первых разделах. Будем называть их теоретическими. Они являются удобным средством развития теории, но не годятся для расчетов: однородных ресурсов не просто много, практически невозможно даже составить их полный список. Например, некоторое изменение свойств какого-нибудь материала делает уже "этот" ресурс "иным".
К другому типу относятся производственные функции, которые можно условно назвать расчетными. Их можно реально построить по наблюдаемым данным и затем использовать для плановых, прогнозных и других расчетов. Каждый аргумент расчетной производственной функции соответствует не однородному, а агрегированному ресурсу.
Степень, агрегирования может быть различной - и очень укрупненной ("труд", "капитал"), и более детальной ("основные рабочие", "специалисты", "здания", "станки" и т. д.) - в зависимости от целей расчета и его обеспеченности статистической информацией.
Заметим, что сказанное относится не только к производственным функциям, но и к другим моделям, используемым в экономике: каждая из них может иметь различные варианты, соответствующие различным уровням абстракции. Теоретические (или, как их еще называют, концептуальные) модели обычно слишком громоздки для численной реализации и к тому же требуют практически недоступного объема числовых данных.
Расчетные модели предполагают укрупненное описание явлений и небезупречны с точки зрения требований строгой теории. Все, что говорилось выше о техническом прогрессе и его представлении на языке производственных функций, относилось к функциям агрегированных факторов. Только в таких случаях можно говорить об увеличении продуктивности фактора вследствие изменения его качества. В теоретической модели изменение качества ресурса - это появление нового вида ресурса. Если исходная производственная функция имела своими аргументами объемы потребления ресурсов п видов, т. е. была функцией га переменных, то появление нового вида ресурса требует использования новой производственной функции, зависящей уже от n + 1 аргумента. Таким образом, для теоретической производственной функции технический прогресс означает увеличение размерности области определения. Исходная производственная функция F(х1, х2,..., хn) не отражает новую ситуацию; новая производственная функция F*(х1, х2,..., хn, хn+1) отражает исходную ситуацию, если положить хn+1 = 0. Связь между производственными функциями описывается равенством:
| F(х1, х2,..., хn) = F*(х1, х2,..., хn, 0). |
Ситуация иллюстрируется рис. 18. Пусть в исходном состоянии фирма использовала только первый вид ресурса, и производственная функция имела вид F(х1); ее изокванты - отмеченные точки на оси х1. Технический прогресс привел к появлению второго ресурса.
Теперь производственная функция имеет вид F*(х1, х2), а ее изокванты - кривые на плоскости х1 х2.
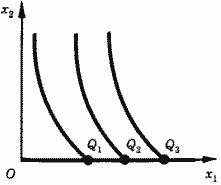
Рис. 18. Карты изоквант: на оси х1 (до появления второго ресурса) и на плоскости х1 х2 (после его появления)
Заметим, что такое представление технического прогресса аналогично описанию короткого и длительного периодов с помощью производственных функций. Новый вид ресурса при этом аналогичен фактору, фиксированному в коротком периоде; единственная особенность состоит в том, что он фиксирован на нулевом уровне (ср. рис. 18 с рис. 12). Поэтому поведение фирмы в условиях технического прогресса иногда называется поведением в сверхдлительном периоде.
Появление нового вида ресурса само по себе еще не означает, что фирма будет его использовать. Если его цена будет слишком высока (изокоста С1 на рис. 19), то задача выбора ресурсов будет иметь угловое решение (точка А1) и фирма откажется от использования нового вида ресурса. При снижении цены фирма начнет его применять наряду с традиционным видом (изокоста С2 и точка А2). Если традиционный вид может быть полностью замещен новым и цена на новый вид ресурса достаточно низка, то задача выбора будет иметь противоположное угловое решение (изокоста С3 и точка А3) - традиционный вид ресурса будет полностью вытеснен новым.
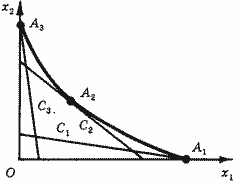
Рис. 19. Изменение выбора ресурсов при снижении цены нового ресурса: отказ от нового (А1), использование нового вместе с традиционным (А2) и вытеснение традиционного новым (А3).
РАЗДЕЛ 4. Штрихи к портрету производственной функции
Современная теория производства сложилась в конце XIX-начале XX в. В явном виде производственная функция была представлена в 1890 г. английским математиком А. Берри (Berry A. The Pure Theory of Distribution // British Association of Advancement of Science: Report of the 60th Meeting, 1890. London, 1893. P. 923-924), помогавшим А. Маршаллу при подготовке математического приложения к его "Принципам экономической науки". Однако попытки установить зависимость выпуска от количества применяемых ресурсов и дать ей какое-то аналитическое выражение имели место задолго до этого. Познакомимся с некоторыми из них.
Марк Теренций Варрон против Марка Порция Катона
В трактате "О земледелии" известный римский писатель и государственный деятель Марк Порций Катон (234-149 гг. до н. э.) описывает две образцовые виллы (хозяйства): оливковую виллу и виноградник (винодельческое хозяйство). Среди множества рекомендаций по их обустройству есть и такие: для обработки оливково рощи в 240 югеров (1 югер равен примерно 3 тыс. м2) Катон определяет необходимое число рабов в 13 человек, включая вилика (управляющего) и вилику (ключницу), а для обработки виноградника в 100 югеров это число составляет 16 человек.
Нормы, предложенные Катоном, вызвали возражение у Марка Теренция Варрона (116-27 гг. до н. э.), столь же известного "писателя по земледелию". Они изложены в его трактате "О сельском хозяйстве". Варрон не соглашается с предположением Катона о том, что между площадью участка и числом рабов, необходимых для его обработки, существует прямая пропорциональная зависимость. Довод Варрона: в общее число рабов Катон не должен был включать вилика и вилику, т. е. расходы по управлению (на содержание управляющего и ключницы), ибо эти расходы постоянны и не зависят от площади участка. "Следовательно, - заключает Варрон, - должно уменьшаться или увеличиваться только число работников и погонщиков быков пропорционально уменьшению или увеличению размера имения". Но и это при условии, "если земля однородна". Если же естественные условия отдельных участков различны, то число рабов будет другим.
Видел Варрон и проблему целочисленности. Он говорил, что Катон предложил меру не единообразную и не нормальную - 240 югеров (нормой является центурия в 200 югеров).
Как, "согласно его наставлению, я мог бы отнять шестую часть от 13 рабов или, оставляя в стороне вилика и вилику, каким образом я мог бы отнять шестую часть от 11 рабов?" (Античный способ производства в источниках. Л., 1933. С. 22).
Таким образом, Варрон по сути дела приходит к выводу о необходимости сопоставления затрат и выпуска как приращений соответствующих переменных, хотя понятие переменной не было, вероятно, ему известно.
Н. Г. Чернышевский
В известных дополнениях к переводу "Оснований политической экономии" Дж. С. Милля, сделанному в 1859 г. для журнала "Современник", Н. Г. Чернышевский так определил задачу экономической науки; "Разложив продукт на доли, соответствующие разным элементам производства, она должна искать, какое сочетание этих элементов и долей дает наивыгоднейший практический результат.
В чем тут состоит задача - понятно каждому: надобно отыскать, при каком сочетании элементов производства данное количество производительных сил дает наибольший продукт" (Чернышевский Н. Г. Очерки из политической экономии (по Миллю) // Избр. экон. произведения: В 3-х т. М., 1949. Т. 3, ч. 2. С. 178). Более того, он предложил и "формулу зависимости производства от двух факторов" (Чернышевский Н. Г. Основания политической экономии Джона Стюарта Милля // Избр. экон. произведения: В 3-х т. М., 1948. Т. 3, ч. 1. С. 306-307), или, как сказали бы мы сейчас, производственную функцию определенного вида.
"Формула", предложенная Чернышевским, проста:
| AB = C, (9) |
где А - "производительные орудия"; В - "работник"; С - "количество продукта известных качеств, производимого дневным трудом этого работника посредством этих орудий".
Коэффициенты при А, В и С характеризуют соответственно "степень достоинства" орудий и работника и "успешность производства". Однако, поскольку сумма коэффициентов при А и В характеризует "данное количество сил, могущих быть обращенными на производство", мы вправе рассматривать их как количество "орудий" и "работников" скорее, чем показатели "степени достоинства" тех и других. Н. Г. Чернышевский приводит и числовую иллюстрацию своей формулы:
1A ∙ 19B = 19C
2A ∙ 18B = 36C
......................
8A ∙ 12B = 96C
9A ∙ 11B = 99C
10A ∙ 10B = 100C
11A ∙ 9B = 99C
12A ∙ 8B = 96C
......................
19A ∙ 1B = 19C
Очевидно, что "производственная функция" Чернышевского является однородной функцией второй степени. Если мы увеличим количество "орудий" и "работников" в k раз, то:
| С* = kAkB = k2AB. |
Следовательно, производство у Чернышевского характеризуется возрастающей отдачей от масштаба. Изокванта функции (9) имеет на графике вид равнобочной гиперболы. Карта изоквант представлена на рис. 20. Норма технической замены "орудиями" "работников" при неизменном выпуске падает (см. таблицу).
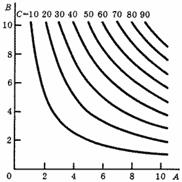
Рис. 20. Карта изоквант производственной функции Н. Г. Чернышевского для различных значений С
Норма технической замены для функции (9) при С = 10
| A | B | RTSAB |
| 10,00 5,00 3,33 2,50 2,00 1,66 1,43 1,25 1,11 1,00 | 1 2 3 4 5 6 7 8 9 10 | - 5,00 1,60 0,83 0,50 0,34 0,23 0,18 0,14 0,11 |
К. Маркс
Взаимосвязь между количествами применяемых ресурсов и объемом выпуска Маркс называл техническим строением капитала. Напомним, что он различал техническое, стоимостное и органическое его строение. Если первое определяется отношением между средствами производства и необходимым для их применения количеством рабочей силы, а второе - тем отношением, в котором капитал распадается на стоимость средств производства и стоимость рабочей силы, то органическим строением капитала Маркс называл его стоимостное строение, "поскольку оно определяется его техническим строением и отражает в себе изменения технического строения" (Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 23. С. 626).
Различая техническое и органическое строение, Маркс писал:
"Первое отношение покоится на техническом базисе и на известной ступени развития производительных сил может рассматриваться как данное. Требуется определенная масса рабочей силы, представленная определенным числом рабочих, чтобы произвести определенную массу продукта, например, в течение одного дня, и, следовательно, - что уже при этом само собой разумеется, - привести в движение, потребить производительно определенную массу средств производства, машин, сырья и т. д....Отношение это очень различно в различных отраслях производства, часто даже в различных подразделениях одной и той же отрасли промышленности, хотя, с другой стороны, в очень отдаленных друг от друга отраслях промышленности оно случайно может быть совершенно или почти одинаковым" (там же. Т. 25, ч. 1. С. 157-158). Достаточно сравнить приведенное определение технического строения капитала с современными определениями производственной функции, чтобы убедиться в их логическом тождестве. Это дает основание использовать в качестве меры технического строения не сами массы капитала (K) и труда (L), а частные дифференциалы простейшей производственной функции Q = f(K, L):
| [(δQ/δK)/(δQ/δL)]∙(K/L) (10) |
Если обозначить цену капитала РK, а цену труда PL и приравнять техническое и стоимостное строение, получим:
| [(δQ/δK)/(δQ/δL)]∙(K/L) = (РK/PL)∙(K/L) (11) |
А это значит, что стоимостное строение капитала можно рассматривать как его органическое строение лишь в том случае, если цены ресурсов пропорциональны их предельной производительности:
| РK/(δQ/δK) = PL/(δQ/δL). (12) |
Поскольку равенство (12) легко приводится к условию оптимальной комбинации ресурсов (7).
Н. Огронович
В 1871 г. в Санкт-Петербурге вышла в свет небольшая книжка с любопытным названием "Новое определение труда и капитала. Наибольшая ценность того или другого, значение наибольшей ценности их в социальной жизни и о наибольшем их производстве, или Новая наука о концентрировании атомов, клеточек, индивидов, ферм в производительных районах с приложением высшей математики". В сущности, это была даже не книга, а "Слово от автора" к будущему труду, который не появился. Автор же книги подписался так: "Н. Огронович (Кудашев, Ху-даш по матери. Воспитанник Киевского университета Св. Владимира)".
Скорее всего, как и книга Г. Госсена (см. лекцию 12, раздел 3), сие "слово" оказалось не замеченным научными кругами. А между тем в ней была сформулирована идея производственной функции практически в современном виде. Н. Огронович пишет: "Труд мой "Наука о концентрировании атомов, индивидов, ферм"... будет по преимуществу не социальный, а политико-экономический, ибо в основу войдет математическая функция, найденная для определения производства; из этой функции мы можем определить maximum и minimum функции, или наибольшее и наименьшее производство всякого организма индивидуального, всякого организма фермы и всякого другого организма.
Потом будет определена прибыль, которая не что иное, как d-л. этой функции... Потом будет определена ценность из этой функции всякой производительной силы, которая есть не что иное, как прибыль, или как d-л производства этой производительной силы, помноженной на то число, какое будет показывать, сколько раз производительная сила участвовала в производстве общем в данный момент производства". С помощью этой функции Огронович хочет в своей будущей книге "определить ценность труда, ценность оборотного капитала, ценность основного капитала и ценность сил природы".
Одновременно Н. Огронович затрагивает и вопрос технического прогресса: "...прогресс производства требует, чтобы капитал все более и более беспредельно рос и разнообразился... Я буду доказывать, что производство будет самым ничтожным образом увеличиваться, если мы будем увеличивать труд, увеличивать напряжение своих мышц... и напротив того, производство наше будет сильно увеличиваться, если мы будем увеличивать капиталы - как оборотный, так и основной и реализованный. Увеличение производства требует увеличения капиталов и уменьшения количества труда. Уменьшить же количество труда - значит уменьшить запрос на труд, и ценность труда упадет" (Огронович Н. Новое определение труда и капитала. СПб., 1873. С. 3).
Таким образом, воспитанник Киевского университета задолго до работ П. Дугласа пришел к идее производственной функции (математической), выразив ее вербально. Но разве основатели австрийской школы политической экономии не сделали того же самого с функцией полезности?
ЗАДАЧИ
1. Производственная функция фирмы q = f(K, L) задана таблицей. Цены факторов РK = 30, РL = 40 не зависят от объемов их потребления фирмой.
Значения производственной функции
| L | K | |||||||||
| 100 120 140 160 180 200 220 240 260 280 300 | 71 79 82 84 86 87 87 88 88 88 88 | 84 100 107 112 115 117 118 119 120 121 122 | 91 112 122 129 134 137 139 141 143 144 145 | 95 119 133 141 147 152 155 158 160 162 164 | 98 125 140 151 158 164 168 171 174 177 179 | 100 129 146 158 166 173 178 183 186 189 191 | 101 132 151 164 174 181 187 192 196 199 202 | 102 135 155 169 180 188 195 200 205 209 212 | 103 137 158 173 185 194 201 207 212 216 220 | 104 139 161 177 189 199 207 213 219 224 228 |
а. Постройте график зависимости q от объема переменного ресурса L при фиксированных значениях К =35; 60; 80.
Постройте графики зависимости q от объема переменного ресурса K при фиксированных значениях L = 100; 200; 300.
Для всех зависимостей проанализируйте изменения среднего и предельного продукта переменного ресурса.
б. Постройте изокванты производственной функции для q = 100; 125; 150; 175; 200.
в. Постройте линию роста фирмы при заданных ценах факторов.
Продукт и ресурсы предполагаются, неограниченно делимыми, а производственная функция - непрерывной. Расчеты и построения могут быть выполнены лишь приближенно.
2. При производстве продукта используются четыре вида ресурсов. В окрестности определенной комбинации; их количеств известны некоторые предельные нормы технической замены: MRTS12 = 0.5; MRTS13 = 5; MRTS24 = 0.1. Найти остальные.
Лекция 23. Затраты
РАЗДЕЛ 0. У БАРБОСА ЕСТЬ ВОПРОСЫ. Что же такое стоимость?
БАРБОС. Не берусь судить обо всех, но мне понятно, что стоимость моего труда, когда я охраняю моего Антона дома и в его директорском кабинете, измеряет, какие усилия моего немалого ума, какой энергии и какого времени стоит для меня эта полезная работа.
АНТОН. Игорь, в этой лекции мы с тобой попробуем заменить термин "затраты" на термин "стоимость".
ИГОРЬ. Именно попробуем. Может, это понравится нашим читателям?
АНТОН. Если они внимательно прочтут Приложение II то возражений быть не должно.
ИГОРЬ. Так что же такое стоимость? И как ее измерить?
АНТОН. Пожалуй, не найти на свете вопросов посложней, чем эти.
ИГОРЬ. Не горюй, Антон. Мы с тобой кое-какие важные слова по этому поводу уже сказали. Помнишь, как в 21-й лекции было рассказано, чту мы теряем и чту находим, когда используем ресурсы для производства деревянной мебели?
АНТОН. Да, да, вспоминаю. Если мы произвели стул, то затраты, ой, извини, стоимость производства, следует измерять как полезность той бумаги, которую можно было бы получить из дерева, использованного на изготовление стула.
ИГОРЬ. Разумеется, и бумаги, и деревянных домов, и шахматных фигур, и еще много другого, что делают из дерева.
АНТОН. А зачем нам сравнивать все эти альтернативные возможности использования дерева?
БАРБОС (ворчит вполголоса, не подымая глаз на хозяина). Зачем, зачем... Самому знать надо как можно больше. А то, помню, героиня одной сказки все время спрашивала: "А зачем тебе большие уши, а зачем тебе большие зубы?". Известно, чем все это кончилось!
ИГОРЬ. Это, чтобы знать, на каком свете живешь, т. е. знать истинно экономические затраты, вернее, истинно экономическую стоимость. Ведь вполне может случиться, что мебель, которую ты хочешь выпускать, в магазинах уже ставить некуда, а вот деревянные коттеджи очень дефицитны.
АНТОН. Теперь я начинаю понимать, в чем дело. Я всегда, таким образом, знаю, на что иду. Скорее всего, при этих обстоятельствах я буду использовать дерево для строительства дефицитных коттеджей. Всякому теперь ясно, что кубометр древесины, вложенный в коттеджи, куда полезнее потребителю, чем кубометр, вложенный куда-нибудь еще.
Дата публикования: 2014-11-18; Прочитано: 308 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
