 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Нормально распределенные случайные величины
|
|
Пусть X случайная величина на пространстве элементарных событий 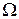 с алгеброй случайных событий
с алгеброй случайных событий 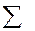 .
.
Определение. Функцией распределения случайной величины X называется функция 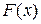 , определяемая равенством
, определяемая равенством
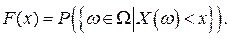
В дальнейшем будем использовать следующие обозначения:
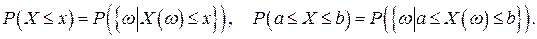
Аналогично определяются вероятности
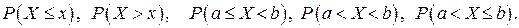
Сформулируем без доказательства основные свойства функции распределения.
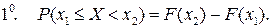
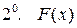 не убывает.
не убывает.
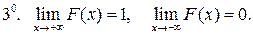
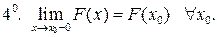 То есть
То есть 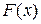 непрерывна слева.
непрерывна слева.
Заметим, что свойство 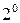 является очевидным следствием свойства
является очевидным следствием свойства 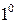 .
.
Задача. Доказать свойства 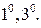
Если X дискретная случайная величина с таблицей распределения (2), то не трудно построить график ее функции распределения 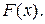
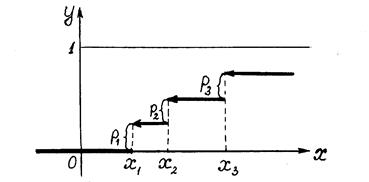
Графиком 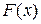 является ступенчатая функция, изображенная на рисунке. Из этого графика видно, что закон распределения случайной величины можно найти через значения функции распределения:
является ступенчатая функция, изображенная на рисунке. Из этого графика видно, что закон распределения случайной величины можно найти через значения функции распределения:
 где
где 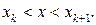 (или
(или 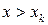 , если
, если 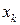 - наибольшее значение X).
- наибольшее значение X).
Таким образом, дискретная случайная величина полностью определяется своей функцией распределения.
Дата публикования: 2014-11-18; Прочитано: 238 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
