Приближенное решение дифференциальных уравнений

Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения можно воспользоваться рядом Тейлора.

Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.

1. Способ последовательного дифференцирования

При решении задачи Коши

,

используется ряд Тейлора

,

где , а остальные производные находятся путем последовательного дифференцирования уравнения и подстановки начальных данных в выражения для этих производных.

Надо отметить, что способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.

Пример 3.12. Найти пять первых членов (отличных от нуля) разложения в степенной ряд решения дифференциального уравнения

, если .

Решение. Находим решение дифференциального уравнения (при 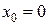) в виде

.

.

.

Далее находим производные высших порядков и значения производных при .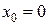

. Тогда .

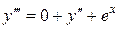. Тогда .

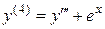. Тогда .

Подставляя найденные значения производных в искомый ряд, получаем:

.

,

1. Способ неопределенных коэффициентов

Этот способ приближенного решения наиболее удобен для линейных дифференциальных уравнений с переменными коэффициентами.

Пусть, например, требуется решить уравнение

с начальными условиями .

Предполагая, что коэффициенты и свободный член разлагаются в ряды по степеням , сходящиеся в некотором интервале , искомое решение находится в виде степенного ряда

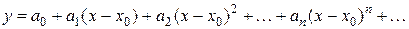
с неопределенными коэффициентами.

При помощи начальных условий находим коэффициенты 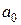и . Для нахождения последующих коэффициентов степенной ряд дифференцируем два раза (каков порядок уравнения) и подставляем выражения для функции и ее производных в исходное уравнение, заменив в нем , их разложениями. В результате получаем тождество, из которого методом неопределенных коэффициентов находим недостающие коэффициенты.

Построенный степенной ряд сходится в том же интервале и является решением исходного уравнения.

Пример 3.13. Найти решение уравнения

.

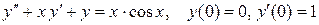используя метод неопределенных коэффициентов.

Решение. Разложим коэффициенты уравнения и при 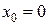в степенные ряды

,

.

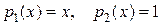Решение исходного дифференциального уравнения находим в виде степенного ряда

.

Тогда

,

.

Из начальных условий находим: . Подставляем полученные ряды в дифференциальное уравнение:

.

Приравнивая коэффициенты при одинаковых степенях :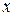

,

,

,

,

,

……………………………

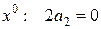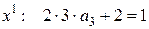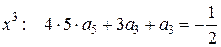Отсюда находим, что , , , , …. Таким образом, получаем решение уравнения в виде

,

т.е. .

,

4. РЯДЫ ФУРЬЕ