Задание 2. Представьте результаты эксперимента, описанного в задаче, в виде таблицы и в виде графика, определите неизвестную величину и ее погрешность графическим методом

Задача 2. При определении жесткости пружины к ее нижнему концу подвешивали грузы известной массы и измеряли соответствующие им удлинения пружины. Экспериментально были получены следующие результаты:

№
F, H
l, мм

Определите жесткость пружины k, учитывая, что при определении силы упругости F абсолютная погрешность (состоящая из приборной погрешности и погрешности отсчета) составила ± 1 Н, а удлинение l измерялось линейкой с ценой деления 1 мм, а приборная погрешность которой

1 мм.

Методические рекомендации по решению задачи

Жесткость пружины k связана с силой упругости F и удлинением l пружины соотношением: 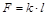(закон Гука), т. е. k является косвенно измеренной величиной при прямых совместных измерениях силы F и удлинения l.

Определение жесткости пружины k и случайной погрешности 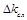данной величины графическим методом, осуществляется следующим образом (см. п. 3.2.1, § 3, гл. 2, раздел II):

1. Строится точечный график, для этого:

§ выбираются оси: по оси у будут откладываться значения F, а по оси х – значения l;

§ выбирается масштаб: М_F: 1мм^{масштабный} – 1Н, М_l: 1мм^{масштабный} – 1мм;

§ по экспериментальным данным строятся точки. В данной задаче значения F и l получены с определенными погрешностями, поэтому на графике следует указать величину этих погрешностей при помощи, например, крестиков (рис. 25),

где 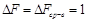Н (по условию задачи),

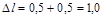, мм.

2. Через нанесенные точки проводится плавная кривая, таким образом, чтобы как над кривой, так и под кривой было одинаковое количество экспериментальных точек. В данном случае может быть получен график, вид которого приближенно показан рис. 26.

3. Определяется наилучшее значение коэффициента .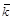

В нашем случае через экспериментальные точки можно провести прямую линию ОА, поэтому для нахождения 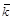следует на данной прямой выбрать точку, например, точку А (рис 26) и рассчитать значение 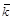по формуле . Численно .

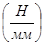4. Находится значение случайной погрешности 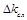. При этом возможны две ситуации:

§ если кривая, проведенная средним образом через все экспериментальные точки, проходит в рамках вычерченных крестиков (которые отображают величину погрешности средств измерений), то это означает, что величина случайной погрешности значительно меньше погрешности средств измерений и поэтому в данном случае, ею можно пренебречь;

§ если кривая, проведенная средним образом через все экспериментальные точки, не пересекает одну или несколько рамок вычерченных крестиков, то значение случайной погрешности больше чем значение погрешности средств измерений и в этом случае ее следует определять соответствующим методом.

В рассматриваемой задаче построенная прямая ОА не проходит в рамках вычерченных крестиков (см. рис. 26). Поэтому нельзя пренебречь случайной погрешностью при нахождении коэффициента k. Тогда значение 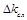определяется графическим методом, следующим образом:

§
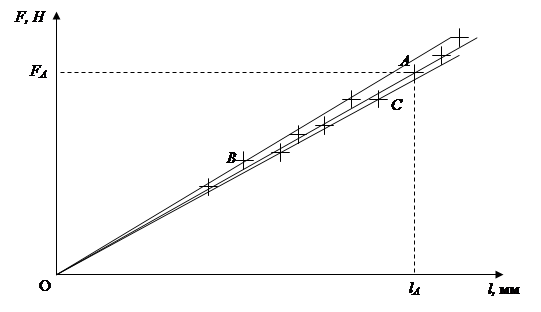построенную прямую поворачивают вокруг начала координат, так, чтобы она, проходя через одну или несколько экспериментальных точек, имела максимальный угловой коэффициент (прямая ОВ рис. 27), а затем поворачивают прямую, так, чтобы она имела минимальный угловой коэффициент (прямая ОС рис. 27).

находятся значения в точке В и в точке С:

, ; , ;

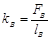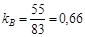
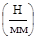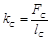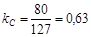
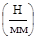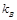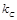§ определяются отклонения и от 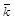по формулам:

, , , ;

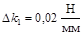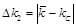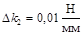§ максимальное из полученных значений и 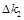принимается за значение случайной погрешности .

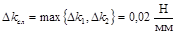5. Для того, чтобы записать окончательный результат в виде предельного интервала, кроме случайной погрешности 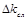, находят погрешность средств измерения и погрешность графической обработки .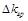

Коэффициент k является косвенно измеренной величиной и определяется из соотношения 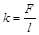(1). Следовательно, для определения можно воспользоваться любым из методов определения погрешности косвенно измеренной величины. В задаче заданы предельные (максимальные) погрешности средств измерений прямо измеренных величин F и l, поэтому для расчета соответствующей погрешности косвенно измеренной величины следует применять один из методов определения предельной (максимальной) погрешности. Найдем погрешность средств измерения коэффициента k при помощи дифференциального метода.

5.1. Выведем формулу для расчета относительной погрешности :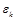

§ найдем натуральный логарифм функции (1): 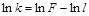(2);

§ продифференцируем выражение (2):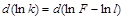

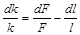(3);

§ в выражении (3) заменим дифференциалы соответствующих функций их абсолютными погрешностями, величину 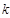заменим ее средним значением, величины 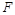и 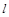заменим их минимальными значениями, т. к. при данных значениях относительная погрешность 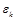при определении величины 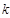будет максимальной (предельной), а алгебраическое суммирование "–" на арифметическое суммирование "+":

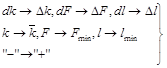получим 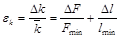(4).

5.2. По формуле (4) рассчитываем значение относительной погрешности средств измерения величины k:

, .

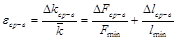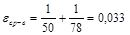5.3. Находим значения абсолютной погрешности средств измерения величины k: , .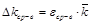

5.4. По формуле (4) рассчитываем значение относительной погрешности графической обработки величины k:

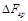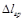, где в качестве и принимаются значения величин, которые в выбранном масштабе соответствуют одному (двум) миллиметрам миллиметровой бумаги: 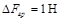, 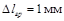. Тогда .

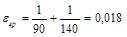5.5. Находим значение абсолютной погрешности графической обработки величины k: , .

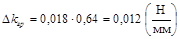5.6. Рассчитываем значение полной абсолютной погрешности:

, .

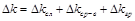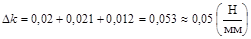5.7. Записываем конечный результата в виде предельного (максимального) интервала: , .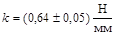

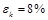Для проверки, правильно ли найдено наилучшее значение коэффициента k, можно рассчитать его при помощи метода наименьших квадратов и сравнить полученные результаты.

Метод наименьших квадратов (см. п. 3.2.2, § 3, гл. 2, раздел II)

1. Рассчитываем наилучшее значение коэффициента k по формуле:

.

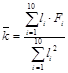При подстановке числовых значений, получаем .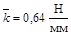

2. Определяем предельную доверительную границу случайной погрешности. Для этого:

2.1. Вычисляем среднюю квадратическую погрешность по формуле:

.

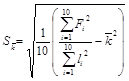Численное значение .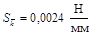

2.2. Рассчитываем предельную доверительную границу случайной погрешности:

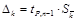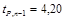, где при .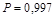

Численное значение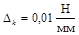

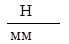
2.3. Записываем результат в виде предельного доверительного интервала: , .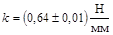

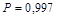Таким образом, можно сделать вывод, что результаты, полученные графическим методом и методом наименьших квадратов совпадают, в пределах найденных погрешностей.