 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 6. Логические основы ЭВМ
|
|
6.1 Основные понятия алгебры логики.
Алгебра логики (или алгебра высказываний) – это раздел математической логики, разработанный в 19 веке в трудах английского математика Джорджа Буля. В алгебре логики используют алгебраические методы для решения логических задач.
Объектами алгебры логики являются высказывания.
Высказывание – это повествовательное предложение, содержание которого можно определить как истинное или ложное. Например, высказывание «Земля – планета Солнечной системы» истинно, а о высказывании «а>b» можно сказать истинно оно или ложно, если указаны значения переменных a b. Алгебра логики отвлекается от смыслового содержания высказываний. Её интересует только один факт – истинно или ложно данное высказывание.
Истинному значению высказывания ставится в соответствие 1(TRUE), ложному 0(FALSE).
Для обращения к высказываниям им назначают имена. Например, А – это высказывание «Ласточки летают низко перед дождём», х1 – «В коробке лежит красный карандаш», х2 – «эта ручка зелёного цвета».
Высказывание абсолютно истинно, если соответствующая ей логическая величина принимает значение 1 при любых условиях Такое высказывание называется тавтологией (логическая константа 1).
Высказывание абсолютно ложно, если соответствующая ей логическая величина принимает значение 0 при любых условиях (логическая константа 0). Такое высказывание называется противоречием.
6.2 Основные логические операции.
- Инверсия – логическое отрицание. Обозначается:
 или х. Читается «не х».
или х. Читается «не х».
Высказывание  истинно при ложном х и ложно при истинном х.
истинно при ложном х и ложно при истинном х.
- Конъюнкция – логическое умножение. Обозначается символами:
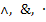 (или знак операции может быть вообще опущен), х1 и х2.
(или знак операции может быть вообще опущен), х1 и х2. - Дизъюнкция – логическое сложение. Обозначается: х1 ٧х2, х1 + х2, х1 или х2.
Эти три операции являются основными.
Остальные операции выражаются через первые три операции: инверсию, конъюнкцию, дизъюнкцию.
- Импликация – логическое следование. Обозначается: х1
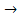 х2. Высказывание х1 -> x2 истинно только тогда, когда правый операнд является истинным, а левый операнд ложным.
х2. Высказывание х1 -> x2 истинно только тогда, когда правый операнд является истинным, а левый операнд ложным. - Эквивалентность(равносильность, необходимо и достаточно). Обозначается: символами
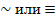 . Высказывание х1~х2 истинно тогда и только тогда, когда операнды равны.
. Высказывание х1~х2 истинно тогда и только тогда, когда операнды равны. - Сложение по модулю 2(исключающее или). Обозначается символом
 .
.
Высказывание истинно тогда и только тогда, когда операнды не равны.
Порядок выполнения операций задаётся круглыми скобками. При отсутствии скобок порядок выполнения операций следующий: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
Составное высказывание (формула алгебры логики, логическое выражение) состоит из нескольких высказываний, соединённых логическими операциями. Исходные высказывания могут быть логическими переменными или логическими константами.
6.3 Основные законы и соотношения алгебры логики.
В алгебре логики имеется четыре основных закона: коммутативный (переместительный), ассоциативный (сочетательный), дистрибутивный (распределительный).
1. Переместительный закон:
· для логического сложения
х1+ х2 = х2 + х1
· для логического умножения
х1 ∙ х2 = х2 ∙ х1
2. Сочетательный закон:
· для логического закона
х1 + (х2 + х3) = (х1 + х2) + х3
· для логического умножения
х1 (х2 х3) = (х1 х2) х3
3. Распределительный закон:
· для логического сложения
х1 (х2 + х3) = х1 х2 + х1 х3
· для логического умножения
х1 + х2 х3 = (х1 + х2) (х1 + х3)
4. Закон общей инверсии (де Моргана):
· для логического сложения
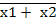 =
=  1 ∙
1 ∙  2
2
· для логического умножения
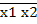 =
=  1 +
1 +  2
2
Справедливость этих законов можно доказать табличным способом, вычисляя значения левой и правой частей доказываемого выражения для всех возможных наборов входных переменных.
Используя основные положения алгебры логики, нетрудно убедиться в справедливости следующих аксиом:
1. х + х + х + х + … + х = х (в алгебре логики нет коэффициентов)
2. х ∙ х ∙ х ∙ … ∙ х (в алгебре логики нет степеней)
3. х + 0 = х
4. х + 1 = 1
5. х ∙ 0 = 0
6. х ∙ 1 = х
7. х ∙  = 0 (закон противоречия)
= 0 (закон противоречия)
8. х +  = 1(закон исключения третьего)
= 1(закон исключения третьего)
Из распределительного закона для логического сложения и умножения вытекают следующие формулы:
· формула склеивания
х1 х2 + х1  2 = х1, т.к. х1(х2 +
2 = х1, т.к. х1(х2 +  2) = х1
2) = х1
· формулы поглощения
х1 + х1 х2 = х1, т.к. х1 (1 + х2) = х1
х1 +  1 х2 = х1 + х2
1 х2 = х1 + х2
 1 + х1 х2 =
1 + х1 х2 =  1 + х2
1 + х2
· формула свёртки
х1х2 +  1 х3+ х2х3 = х1х2 +
1 х3+ х2х3 = х1х2 +  1 х3
1 х3
6.4 Логические функции двух переменных.
Логическая функция (функция алгебры логики ФАЛ) - функция f(x1, x2, …, xn), принимающая значение, равное нулю или единице на наборе логических переменных x1, x2, …, xn.
Логическую функцию можно задать двумя способами: логической формулой или таблицей истинности. Таблица истинности задаёт значения функции на всех возможных наборах её переменных.
В алгебре логики строго доказывается, что для n переменных количество различных наборов равно2n,а количество логических функций для n переменных равно 2 в степени 2n Рассмотрим все возможные наборы для одной переменной, для двух и трёх переменных.
Для одной переменной таких наборов два:0,1.
Для двух переменных наборов четыре:
0 0
0 1
1 0
1 1
Для трёх переменных наборов восемь:
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
В таблице 6.1. представлены различные логические функции двух переменных.
Таблица 6.1. Логические функции двух переменных
| X1 | X2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
1. Конъюнкция (логическое умножение, союз и) – функция f1(x1,x2). Принимает значение истина тогда и только тогда, когда обе переменные истинны. Во всех остальных случаях принимает значение ложь. Обозначается символами: 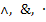 (или знак операции может быть вообще опущен). В общем случае функцию конъюнкция можно определить для n аргументов, т.е. x1, x2, …, xn.
(или знак операции может быть вообще опущен). В общем случае функцию конъюнкция можно определить для n аргументов, т.е. x1, x2, …, xn.
2. Дизъюнкция (логическое сложение, функция ИЛИ) – функция f7(x1, x2). Принимает значение ноль тогда и только тогда, когда оба аргумента равны нулю и принимает значение 1, если хотя бы один аргумент равен 1. Обозначается символом +. В общем случае функцию можно определить для n аргументов.
3. Импликация (следование) х1 в х2 функция f13. Обращается в ноль только в том случае, когда переменная х1 равна единице, а переменная х2 равна нулю. Обозначается х1 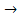 х2.
х2.
4. Импликация х2 в х1 – функция f11(x1, x2). Обращается в ноль тогда и только тогда, когда х2 равен 1, а х1 равен 0.
5. Эквиваленция (разнозначность) – функция f9 (x1, x2). Обращается в 1 тогда и только тогда, когда обе переменные одновременно принимают одинаковые значения. Обозначается символами 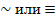 .
.
6. Исключающее или (сложение по модулю 2), функция f6 (x1, x2). Принимает значение истина в том и только в том случае, когда только один из аргументов равен 1. Обозначается символом 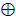 .
.
7. Штрих Шеффера – функция f14 (x1, x2). Принимает значение 0 тогда и только тогда, когда оба аргумента одновременно равны 1. Во всех остальных случаях функция равна 1. Обозначается символом /. F14 (x1, x2) = x1 / x2. Немецкий математик Д. Шеффер на основе этой функции создал алгебру, названную алгеброй Шеффера.
8. Стрелка Пирса (элемент Вебба) – функция f8 (x1, x2). Обозначается символом ↓: f8 (x1, x2) = x1 ↓ x2. Математики Ч. Пирс и Д. Вебб независимо друг от друга изучавшие свойства этой функции, создали алгебру, названную алгеброй Пирса (Вебба).
9. Отрицание импликации (коимпликация) х1 в х2, функция f2 (x1, x2). Принимает значение 1 тогда и только тогда, когда х1 равен 1, а х2 равен 0. Обозначается 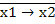 , или х1
, или х1 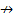 х2. Данную функцию можно рассматривать как функцию запрета со стороны переменной х2.
х2. Данную функцию можно рассматривать как функцию запрета со стороны переменной х2.
10. Отрицание импликации (коимпликация) х2 в х1, функция f4 (x1, x2). Принимает значение 1 тогда и только тогда, когда х2 равен 1, а х1 равен 0. Во всех остальных случаях значение функции 0. Функцию f4 (x1, x2) можно рассматривать как функцию запрета со стороны переменной х1.
Оставшиеся шесть логических функций f0, f3, f5, f10, f12, f15 являются либо константами, либо функциями существенным образом зависящие только от одной из переменных х1 или х2.
f0 (x1, x2) ≡ 0;
f15 (x1, x2) ≡ 1;
f3 (x1, x2) = x1;
f5 (x1, x2) = x2;
f12 (x1, x2) = 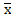 1;
1;
f10 (x1, x2) =  2.
2.
Все перечисленные логические функции являются элементарными. Приведем некоторые определения:
Определение 1. Две функции равносильны друг другу, если на всех возможных наборах переменных принимают одни и те же значения.
Определение 2. Функция [f(x1, x2, …, xn)]*, равная 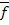 (
(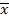 1,
1, 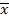 2, …,
2, …, 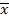 n) называется двойственной функцией к функции f(x1, x2, …, xn).
n) называется двойственной функцией к функции f(x1, x2, …, xn).
6.5 Свойства функций алгебры логики
1. Функция штрих Шеффера { / }.
Свойства функции штрих Шеффера х1 / х2 = 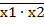 =
=  1 +
1 + 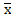 2
2
· х / х = 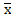 (т.к. х / х =
(т.к. х / х = 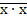 =
=  )
)
· х / 1 = 
· х / 0 = 1
·  / 1 = х
/ 1 = х
·  / 0 = 1
/ 0 = 1
· х /  = 1
= 1
· Для функции штрих Шеффера справедливо свойство коммутативности для двух переменных, т.е. х1 / х2 = х2 / х1
Очередность операций для функции штрих Шеффера с n переменными устанавливается с помощью скобок.
Свойства ассоциативности и дистрибутивности для функции штрих Шеффера не справедливы.
2. Функция стрелка Пирса 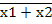 =
=  1 +
1 +  2 = х1 ↓ х2
2 = х1 ↓ х2
· х ↓ х =  (т.к. х ↓ х =
(т.к. х ↓ х = 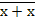 =
=  )
)
· х ↓ 0 = 
· х ↓ 1 = 0
· х ↓  = 0
= 0
·  ↓ 1 = 0
↓ 1 = 0
·  ↓ 0 = х
↓ 0 = х
· х1 ↓ х2 = х2 ↓ х1 свойство коммутативности выполняется только для двух переменных.
Для установления приоритетов выполнения операции стрелка Пирса, обязательно должны использоваться скобки.
Для функции стрелка Пирса свойства ассоциативности и дистрибутивности несправедливы.
3. Функция сложение по модулю 2 (х1 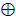 х2).
х2).
Через отрицание, конъюнкцию и дизъюнкцию функция сложения по модулю 2 выражается следующим образом:
| х1 | х2 | х1 ⊕ х2 | СДНФ |
 1 х2 1 х2
| |||
х1  2 2
| |||
х1 ⊕ х2 = х1  2 +
2 +  1 х2;
1 х2;
Функция сложения по модулю 2 обладает следующими свойствами:
· коммутативности х1 ⊕ х2 = х2 ⊕ х1
· ассоциативности х1 ⊕ (х2 ⊕ х1) = (х1 ⊕ х2) ⊕ х3
· дистрибутивности х1 (х2 ⊕ х3) = х1 х2 ⊕ х1 х3
Для этой функции справедливы аксиомы:
х ⊕ х = 0
х ⊕ 1 = 
х ⊕  = 1
= 1
х ⊕ 0 = х
х1 ⊕ х2 =  1 ⊕
1 ⊕  2
2
х1 ⊕  2 = х1~ х2
2 = х1~ х2
 1 ⊕ х2 = х1 ~ х2
1 ⊕ х2 = х1 ~ х2
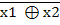 = х1 ~ х2
= х1 ~ х2
На основании аксиом и свойств можно вывести правила перевода функций отрицание, конъюнкция, дизъюнкция через функцию сложения по модулю 2 и наоборот.
 1 = х1 ⊕ 1;
1 = х1 ⊕ 1;
х1 + х2 = х1 ⊕ х2 ⊕ х1 х2
х1 х2 = (х1 ⊕ х2) ⊕ (х1 + х2)
4. Функция равнозначности (х1 ~ х2) выражается через отрицание, конъюнкцию и дизъюнкцию следующим образом:
| х1 | х2 | х1 ~ х2 | СДНФ |
 1 1  2 2
| |||
| х1 х2 |
х1 ~ х2 = х1 х2 +  1
1  2
2
Свойства функции равнозначности:
· х ~ х = 1
· х ~ 0 = 
· х ~ 1 = х
· х ~  = 0
= 0
· х1 ~ х2 =  1 ~
1 ~  2
2
· х1 ~  2 = х1 ⊕ х2
2 = х1 ⊕ х2
·  1 ~ х2 = х1
1 ~ х2 = х1 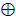 х2
х2
· 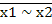 = х1 ⊕ х2
= х1 ⊕ х2
· Для двух переменных выполняется свойство коммутативности
х1 ~ х2 = х2 ~ х1
Свойства ассоциативности и дистрибутивности для этой функции не выполняются.
Функция импликация (х1 → х2) выражается через отрицание и дизъюнкцию следующим образом:
| х1 | х2 | х1 → х2 | СКНФ |
 1 + х2 1 + х2
| |||
х1 → х2 =  1 + х2
1 + х2
Для функции импликации справедливы аксиомы:
х → х = 1
х → 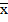 =
= 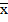
х → 1 = 1
0 → х = 1
х → 0 = 
1 →  =
= 
х1 → х2 =  2 →
2 →  1
1
х1 ∙ х2 = 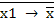 2
2
х1 + х2 =  1 → х2 =
1 → х2 =  2 → х1
2 → х1
Свойства коммутативности, ассоциативности и дистрибутивности для этой функции не справедливы.
5. Функция коимпликация (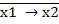 ) выражается через отрицание и конъюнкцию следующим образом:
) выражается через отрицание и конъюнкцию следующим образом:
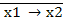 = х1
= х1  2
2
Для функции коимпликации справедливы аксиомы:
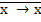 = 0
= 0
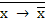 = х
= х
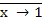 = 0
= 0
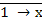 =
= 
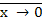 = х
= х
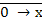 = 0
= 0
х1 + х2 = 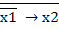
х1 х2 = 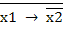
6.6 Аналитическое представление логических функций.
Рассмотренное выше представление логических функций наглядно и может быть применено для функций от любого количества переменных, однако такая запись не является компактной при анализе свойств функций алгебры логики. Проще выглядит аналитическая запись в виде формул. Но наиболее рациональным является представление логических функций в так называемых нормальных формах. Основу этих формул составляют понятия элементарных конъюнкций и дизъюнкций.
Элементарная конъюнкция (минтерм) образуется конъюнкцией конечного множества логических переменных и их инверсий, например:
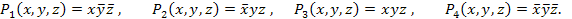
Элементарная дизъюнкция (макстерм) образуется дизъюнкцией конечного множества логических переменных и их инверсий, например:
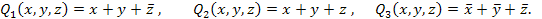
Элементарная конъюнкция принимает единичное значение только при одном из всех возможных наборов входных переменных, а элементарная дизъюнкция принимает нулевое значение только при одном из возможных наборов аргументов и единичное значение при всех других.
Следовательно, минтерм алгебраически представляет собой конъюнкцию аргументов и их инверсий, а макстерм – дизъюнкцию аргументов и их инверсий.
Количество минтермов и макстермов совпадает с количеством возможных наборов аргументов. В таблице 6.2. приведены значения элементарных конъюнкций и дизъюнкций для двух аргументов.
Таблица 6.2. Элементарные конъюнкции и дизъюнкции двух переменных
| Значения аргументов | Значения элементарных конъюнкций | Значения элементарных дизъюнкций | |||||||
| X | Y | 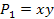
| 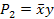
| 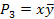
| 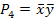
| 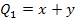
| 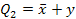
| 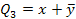
| 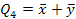
|
Количество аргументов, образующих элементарную конъюнкцию или дизъюнкцию называется ее рангом. Например, ранг минтерма 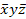 равен 3.
равен 3.
Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется нормальной.
Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции.
Т.е. нормальная форма – это объединение термов, включающее минтермы переменного ранга.
Количество всех термов, входящих в состав ДНФ равно количеству единичных строк таблицы истинности заданной функции.
Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции (макстермы), связанные между собой операцией конъюнкции.
1. Совершенные нормальные формы.
Одну и ту же логическую функцию можно представить различными ДНФ и КНФ. Из всей совокупности нормальных форм выделяют одну ДНФ и одну КНФ, а именно такие формы, которые являются инверсными по отношению друг к другу, т.е. если одна из них равна «1», то другая при этом равна «0», и наоборот. Эти формы называются совершенными нормальными формами.
Дизъюнктивная совершенная нормальная форма (СДНФ) отвечает следующим требованиям:
- в ней нет двух одинаковых элементарных конъюнкций;
- ни одна конъюнкция в ней не содержит одинаковых переменных;
- ни одна конъюнкция не содержит двоичную переменную с ее инверсией;
- все конъюнкции являются элементарными;
- все конъюнкции имеют одинаковый ранг.
Для представления функции в СДНФ может быть использована также операция Å.
Сформулируем требования, которые предъявляются к операции связывающей элементарные минтермы:
1) Если какой-либо терм 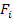 = 1, то функция должна быть равна 1.
= 1, то функция должна быть равна 1.
2) Если какой-либо терм 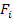 = 0, то функция может быть равна 1.
= 0, то функция может быть равна 1.
3) Необходимо, чтобы при значениях термов 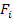 = 0 функция была равна нулю.
= 0 функция была равна нулю.
Табличное представление операций отвечающих требованиям имеет вид, представленный в таблицах 6.3. и 6.4.3:
Таблица 6.3. Таблица6.4.
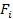
| 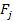
| D=+ |
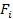
| 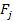
| D=Å |
Любая таблично заданная ФАЛ может быть представлена в следующей аналитической форме:
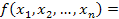
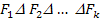 , где
, где
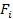 - элементарный минтерм; знак D обозначает операции +, Å;
- элементарный минтерм; знак D обозначает операции +, Å;
k – количество наборов, на которых функция равна 1.
Конъюнктивная совершенная нормальная форма (КСНФ) отвечает следующим требованиям:
- в ней нет двух одинаковых элементарных дизъюнкций;
- ни одна дизъюнкция в ней не содержит двух одинаковых переменных;
- ни одна дизъюнкция не содержит переменную вместе с ее инверсией;
- все дизъюнкции имеют один и тот же ранг.
Чтобы определить, какие операции могут связывать элементарные дизъюнкции, изложим следующие требования:
1) Если какой-либо терм 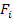 = 0, то функция должна быть равна 0.
= 0, то функция должна быть равна 0.
2) Если все термы 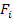 = 0, то функция равна 1.
= 0, то функция равна 1.
Выполняя эти требования можно привести к операциям конъюнкции и равнозначности (таблица 6.5. и 6.6):
Таблица 6.5. Таблица 6.6.
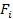
| 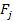
| & |
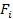
| 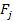
| º |
Вывод: любая таблично заданная ФАЛ может быть задана в аналитической форме:
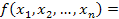
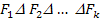 , где
, где
знак D обозначает операции & и º, k – количество двоичных наборов, для которых 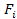 =0.
=0.
В алгебре логики строго доказывается, что любая логическая функция, кроме 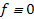 , представима в ДСНФ, любая функция, кроме
, представима в ДСНФ, любая функция, кроме 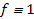 , представима в КСНФ.
, представима в КСНФ.
Формулы в ДСНФ или КСНФ можно получить по табличному представлению логической функции.
Для образования ДСНФ необходимо выполнить следующие действия:
1) по каждому набору двоичных переменных, при котором логическая функция принимает значение 1, составить элементарные конъюнкции;
2) в элементарные конъюнкции записать без инверсии переменные, заданные единицей в соответствующем наборе, и с инверсией – переменные заданные нулем;
3) соединить элементарные конъюнкции знаком операции дизъюнкции или операции сложение по модулю 2.
Для образования КСНФ необходимо выполнить аналогичную последовательность действий:
1) по каждому набору двоичных переменных, при котором логическая функция принимает значение 0, составить элементарные дизъюнкции;
2) в элементарные дизъюнкции записать без изменения переменные, заданные нулем в соответствующем наборе, и с инверсией – переменные заданные единицей;
3) соединить элементарные дизъюнкции знаком конъюнкции.
Пример.
Пусть задана некоторая функция 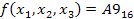 (см таблицу 6)
(см таблицу 6)
Получим для заданной функции СДНФ и СКНФ.
Функция 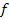 принимает значение 1 для четырех наборов и значение 0 для других четырех наборов.
принимает значение 1 для четырех наборов и значение 0 для других четырех наборов.
| Значения аргументов | Значения функции | ДСНФ | КСНФ | ||
| X | Y | z | 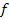
| ||
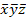
| - | ||||
| - | 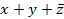
| ||||
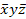
| - | ||||
| - | 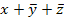
| ||||
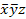
| - | ||||
| - | 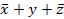
| ||||
| - | 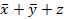
| ||||
| xyz | - |
Функция в СДНФ состоит из логической суммы четырех элементарных конъюнкций третьего ранга:
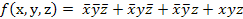
Функция в СКНФ является логическим произведением четырех элементарных дизъюнкций третьего ранга:
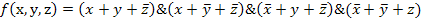
Совершенная нормальная форма отличается от нормальной формы тем, что всегда содержит термы только максимального ранга и дает однозначное представление функции.
Произвольная нормальная дизъюнктивная форма переводится в СДНФ следующим образом:
пусть 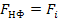 , тогда
, тогда
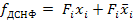 , где
, где 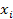 - переменная, которая не входит в данный терм
- переменная, которая не входит в данный терм 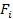 .
.
Пример.
Логическую функцию, заданную в ДНФ преобразовать в СДНФ.
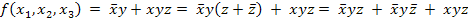 .
.
Произвольная КНФ переводится в СКНФ логическим умножением дизъюнкции младшего ранга на конъюнкцию 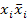 , где
, где 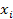 – переменная, которая не входит в данный терм.
– переменная, которая не входит в данный терм.
Пусть 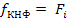 , тогда
, тогда
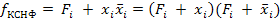
Пример.
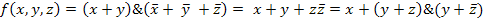
При использовании аналитических форм представления обычно стремятся к упрощению логических функций.
6.7 Системы функций алгебры логики.
Рассмотрим теорему Жегалкина, которая играет важную роль в алгебре логики.
Теорема Жегалкина. Любая булева функция может быть представлена многочленом вида 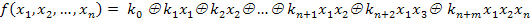 , где
, где 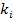 – коэффициент, принимающий значения 0 или 1.
– коэффициент, принимающий значения 0 или 1.
Теорема Жегалкина дает возможность представить любую логическую функцию в виде полиномов разной степени, существует несколько классов ФАЛ, которые также важны для логического анализа.
Класс линейных функций ( 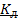 ). Булева функция называется линейной, если она представляется полиномом первой степени:
). Булева функция называется линейной, если она представляется полиномом первой степени:
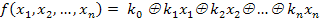 .
.
Количество линейных функций равно 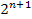 .
.
Например, при n=2 количество линейных функций равно 8.
1) 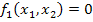 ;
;
2) 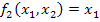 ;
;
3) 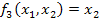 ;
;
4) 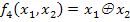 ;
;
5) 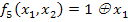 ;
;
6) 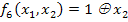 ;
;
7) 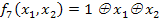 ;
;
8) 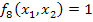 .
.
Класс функций, сохраняющих 0 ( 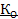 ).
).
Если функция на нулевом наборе переменных равна нулю, то говорят, что функция сохраняет ноль:
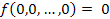 .
.
Класс функций, сохраняющих 1 ( 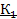 ).
).
Если функция на единичном наборе переменных равна 1, то говорят, что функция сохраняет единицу:
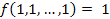 .
.
Класс монотонных функций ( 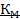 ).
).
Функция алгебры логики называется монотонной, если при любом возрастании набора значения этой функции не убывают.
Класс самодвойственных функций ( 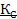 ).
).
Функция алгебры логики является самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, т.е.:
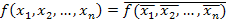 .
.
Все названные функции обладают существенным свойством: любая функция алгебры логики, полученная с помощью операции суперпозиции и подстановки из функций одного класса, обязательно будет принадлежать этому же классу. При этом система логических функций называется функционально полной, если любую логическую функцию можно представить в аналитической форме через функции, взятые в любом конечном числе экземпляров каждая.
Базисом называется полная система ФАЛ, с помощью которой любая ФАЛ может быть представлена суперпозицией исходных функций.
Теорема Поста-Яблонского. Для того, чтобы система ФАЛ была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию:
не сохраняющую ноль,
не сохраняющую единицу,
не являющуюся линейной,
не являющуюся монотонной,
не являющуюся самодвойственной.
Проблема простейшего представления логических функций сводится не только к выбору не только базиса, но и формы наиболее экономного представления этих функций.
Дата публикования: 2014-11-04; Прочитано: 1998 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
