 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 4. Арифметические основы ЭВМ
|
|
4.1 Системы счисления
Информация, обрабатывая ЭВМ и находящаяся внутри вычислительной машины, всегда представлена в виде чисел, записанных в той или иной системе счисления. Вопрос о выборе системы счисления для цифрового автомата - один из важнейших вопросов проектирования как алгоритмов функционирования отдельных устройств, так и расчёта технических характеристик автомата.
Можно считать, что любое число имеет значение (содержание) и форму представления(т. е. запись числа). Значение числа задает порядок расположения чисел на числовой оси, или другими словами его отношение к значениям других чисел («больше», «меньше», «равно»). Форма представления определяет порядок записи числа с помощью предназначенных для этого знаков. При этом значение числа не зависит от способа его представления. Это означает также, что число с одним и тем же значением может быть записано по-разному, т.е. отсутствует взаимно однозначное соответствие между представлением числа и его значением. Например, число пять в римской системе счисления представляется как символ «V», в двоичной системе счисления как набор символов – цифр «101», в десятичной системе счисления как символ – цифра «5» и т.д., этот ряд можно продолжать бесконечно. В связи с этим возникают вопросы, во-первых, о формах представления чисел, и, во-вторых, о возможности и способах перехода от одной формы к другой.
Способ представления числа определяется системой счисления.
Система счисления – совокупность приёмов и правил для записи числа символами(цифровыми знаками).
Любая предназначенная для практического применения система счисления должна обеспечивать единственность представления числа и простоту оперирования числами.
Способы записи чисел можно объединить в две группы: непозиционные и позиционные. В свою очередь позиционные системы счисления подразделяются на традиционные системы счисления и нетрадиционные системы счисления.
Непозиционные системы счисления.
Системы счисления, в которых каждой цифре соответствует величина, независящая от местоположения этой цифры в записи числа, называются непозиционными.
Принципы построения таких систем не сложны. Для их образования используют в основном операции сложения и вычитания.
К непозиционным системам счисления можно отнести унарную систему. Система с одним символом(палочкой) встречалась у многих народов.
Наиболее известная непозиционная система счисления - римская. В римской системе счисления для изображения чисел используются символы I, V, X, L(50), C(100), D(500),М(1000). Десятичное число 27 представляется следующим образом: XXVII=10+10+5+1+1. В непозиционных системах счисления не представляются дробные и отрицательные числа. Арифметические операции выполнять в непозиционной системе счисления очень сложно, так как отсутствуют правила для выполнения действий.
Позиционные системы счисления.
Системы счисления, в которых вклад каждой цифры в величину числа зависит от ее положения (позиции) в последовательности цифр, изображающей число, называются позиционными. Для позиционных систем счисления характерным и определяющим является наличие основания системы, которое показывает, во-первых, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию(влево или вправо) и, во-вторых, какое количество различных цифр входит в ограниченный набор, называемый алфавитом системы, используемый для записи любого числа.
Под алфавитом позиционной системы счисления понимают совокупность различных цифр (символов), используемых для записи чисел.
Для записи чисел в конкретной системе счисления используется некоторый конечный алфавит, состоящий из цифр - символов.
При этом основанием традиционной системы счисления может быть любое натуральное число р³2. Наименование системы счисления соответствует ее основанию. Количество цифр, используемых в р-ичных системах счислениях для записи алфавита равно основанию системы счисления Например, алфавит двоичной системы счисления состоит из двух цифр 0 и 1. Алфавит двенадцатеричной системы счисления состоит из 12 цифр-символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Традиционных цифр-символов для записи алфавита этой системы счисления оказалось недостаточно, поэтому были введены в качестве цифр заглавные буквы латинского алфавита.
В теории чисел рассматриваются системы счисления, основаниями которых могут быть любые натуральные числа>1, а также доказывается, что в любой позиционной системе счисления можно записать любое число и притом единственным образом.
Запишем алфавиты систем счисления, используемых в информатике:
- двоичная система счисления 0,1;
- четверичная система счисления 0,1,2,3;
- восьмеричная система счисления 0,1,2,3,4,5,6,7;
- шестнадцатеричная система счисления 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
Любое число А в позиционной системе счисления можно представить суммой произведений целых однозначных коэффициентов ai, взятых из алфавита системы на последовательные целые степени основания p (так называемая развернутая форма записи числа):
 , (4.1)
, (4.1)
где m — количество цифр в целой части числа или Аq= 
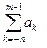 ×qk, для целой части числа и Аq=
×qk, для целой части числа и Аq= 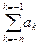 ×qk (4.2)
×qk (4.2)
где ак-любая цифра из алфавита системы с основанием равным q, m, n-число позиций соответственно для целой и дробной частей числа.
Степенной ряд для целой и дробной частей числа можно представить эквивалентными выражениями по схеме Горнера:
для целой части: Аq= 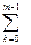 ak×qk=(…((am-1q+am-2q)q+am-3)q+…+a1)q+a0; (4.3)
ak×qk=(…((am-1q+am-2q)q+am-3)q+…+a1)q+a0; (4.3)
для дробной части Aq= 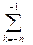 akqk=q-1(a-1+q-1(a-2+…q-1 (a-k+1+a-kq-1)…)). (4.4)
akqk=q-1(a-1+q-1(a-2+…q-1 (a-k+1+a-kq-1)…)). (4.4)
4.2 Перевод чисел из одной системы счисления в другую.
1) Перевод целых чисел из одной системы счисления в другую.
Целое число в системе счисления q может быть представлено эквивалентным числом в системе счисления р по формуле (1.3)
Аq=Ар=(…((bm-1p+bm-2p)q+bm-3)p+…+b1)p+b0. (4.5)
Задача перевода числа из одной системы счисления(q) в другую систему счисления (р) заключается в отыскании значений цифр bk числа в новой системе счисления.
Разделив обе части равенства (4.5) на основание новой системы р, выраженное цифрами системы счисления q, получим:
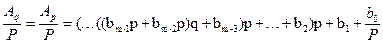 (4.6)
(4.6)
или Аq=Ap=(Aq)1+b0, где (Аq)1 – целое частное, b0 – остаток, являющийся первой младшей цифрой числа в новой системе счисления, остаток выражен цифрами исходной системы счисления.
При следующем делении частного на основание системы счисления р будут получены новое частное и новый остаток: (Аq)1=(Aq)2+b1, где b1 – вторая младшая цифра числа. Продолжая деление целых целых частных до нулевого значения частного, находим все цифры числа в новой системе счисления.
Правило перевода целого числа из одной системы счисления в другую.
1) последовательно делить данное число и получаемые целые частные на основание новой системы счисления, выраженные цифрами исходной системы, до тех пор, пока частное не станет равным нулю.
2) Полученные остатки, являющиеся цифрами числа в новой системе счисления, выразить цифрами алфавита этой системы счисления.
3) Записать число в новой системе, начиная с последнего остатка.
2) Перевод дробных чисел.
Рассуждая по аналогии с переводом для целых чисел, но используя операцию умножения, сформулируем правило перевода дробных чисел.
Правило перевода дробных чисел из одной системы счисления в другую.
1) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы, выраженное цифрами исходной системы, до тех пор, пока либо дробная часть произведения не станет равной нулю, либо не появится период, либо не будет достигнуто заданное количество разрядов искомой дроби.
2) Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, выразить цифрами алфавита этой системы.
3) Записать дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
4.3 Перевод из 10-ной системы счисления в р-ную.
1.) Используем изложенный способ перевода числа из одной системы счисления в другую при р=10 и q=2.
Пусть десятичное число равно 13. Чтобы перевести его в двоичную систему счисления необходимо проделать следующие арифметические операции:
  1 1
| ||||||
Число 13 делим на 2, полученный остаток будет младшим разрядом искомого двоичного числа.
Каждое очередное частное делится на 2 до тех пор, пока частное от деления не станет не станет равным 0.
Последнее частное является старшим разрядом двоичного числа. Запишем полученное последнее частное и все остатки по порядку справа—налево — 1101, это и есть число 13 в двоичной системе счисления, 1310=11012.
Сущность вычислений заключается в многократном делении целых чисел на 2.
Рассмотрим перевод дробного десятичного числа в двоичную форму. Для этого мы должны проделать арифметическую операцию умножения до первого полученного нуля в дробной части, либо до определенного количества значащих цифр.
Поясним на примерах.
1) переведем число 0,5 (десятичное) в двоичную систему счисления. Для наглядности будем приводить умножение «столбиком».
 0 0
| |
2) 0,7510 переводим в двоичную систему счисления.
 |
 0 0
| 75 2 |
| 50 2 | |
Выписываем разряды «сверху—вниз».
3) 0,3310 переводим в двоичную систему.
 0 0
| 33 2 |
| 66 2 | |
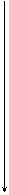 1 1
| 32 2 |
| 64 2 | |
| 28 2 | |
| 56 2 | |
| 12 2 | |
| 24 2 | |
| 48 2 | |
| 96 2 | |
| 92... |
4) Перевести 10,2510 в двоичную систему счисления.
| 0, | 25 2 |
| 50 2 | |
| 0 |
10,2510=1010,012.
2.) Выполнить перевод числа из одной системы счисления в другую можно подбором соответствующих показателей основания системы счисления и коэффициентов при этих степенях, т. е. записать развернутую форму числа, но уже в другой системе счисления. Наиболее легко этот способ реализуется для двоичной системы счисления, так как коэффициенты при степенях могут принимать значения либо 0, либо 1. Например, переведем число 123 в двоичную систему счисления подбором показателей степеней и коэффициентов при них. Составим таблицу степеней числа 2 и посмотрим, какие из этих степеней могут в сумме составить число 123.
Таблица степеней числа 2.
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 |
123=64+32+16+8+2+1=1×26+1×25+1×24+1×23+0×22+1×21+1×20=11110112.
Рассмотрим перевод целых и дробных чисел из десятичной системы счисления в восьмеричную систему счисления.
В восьмеричной системе счисления для представления числа используются цифры от 0 до 7. Правила перевода естественно остаются прежними.
Пример
21,2510 переведем в восьмеричную систему счисления.
| 2110=258 0,2510=0,28 21,2510=25,28 |
| 25 8 | |
При переводе из десятичной системы счисления в шестнадцатеричную, необходимо помнить о том, что количество символов алфавита шестнадцатеричной системы счисления превышает количество символов алфавита десятичной системы счисления и двузначные числа 11,12,13,14,15 десятичной системы счисления являются однозначными в системе счисления по основанию 16.
В шестнадцатеричной системе счисления для записи любого числа необходимо 16 цифр, для изображения недостающих цифр используются заглавные буквы латинского алфавита.
Алфавит шестнадцатеричной системы счисления:
| A | B | C | D | E | F | ||||||||||
Пример.
Перевести десятичное число 142,25 в шестнадцатеричную систему счисления.
| 14210=8E8 0,2510=0,416 142,2510=8E,416 |
| (E) |
| 0, | 25 16 |
4.4 Перевод чисел из р-ичной системы счисления в десятичную.
Для того, чтобы перевести р-ичное число в десятичную систему счисления, запишем его в развернутой форме, а затем, выполнив необходимые вычисления, получим соответствующее десятичное число.
Пример 1.
Перевести из восьмеричной системы счисления в десятичную следующие числа:
-13.48; 27.518; 14.28; 127.038
Запишем развернутую форму записи числа в восьмеричной системе счисления, основание системы счисления108, выразим цифрой десятичной системы счисления 108=810
Выполним перевод для первого числа:
-13.48= -(138+0.48)
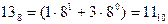
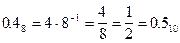
-13.48= -11.510.
Остальные примеры решите самостоятельно.
Пример 2.
Перевести следующие числа: 1110011.012, -456.078, 1АС.1516.
1110011.01=1×26+1×25+1×24+0×23+0×22+1×21+1×20+
0×2-1=64+32+16+2+1+0.25=115.25; остальные примеры выполните самостоятельно.
4.5 Системы счисления с основаниями, являющимися степенью 2.
При решении примеров по переводу чисел из одной системы счисления в другую (при этом обе системы имеют в качестве основания степени числа 2) может понадобиться таблица переводов.
Таблица переводов.
Дата публикования: 2014-11-04; Прочитано: 699 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
