Тема 7. Анализ взаимосвязей

При анализе связей между показателями особое внимание уделяется вероятностным связям. Для выявления их наличия и определения тесноты используется корреляционно-регрессионный анализ, метод параллельных рядов, графический метод, методы анализа атрибутивных и альтернативных рядов.

При проведении корреляционно-регрессионного анализа выделяют следующие этапы:

1. подбирается уравнение регрессии, и рассчитываются его параметры;

2. определяются показатели тесноты связи;

3. устанавливается сила связи;

4. оценивается надежность параметров уравнения регрессии и показателей тесноты связи.

На первом этапе выбирают уравнение регрессии. Для этого можно воспользоваться графическим методом, изобразив эмпирические значения факторного и результативного признака на оси координат.

Если наблюдается линейная связь между признаками, рекомендуется воспользоваться уравнением прямой:

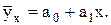(7.1)

При наличии нелинейных форм связи можно использовать следующие уравнения:

- параболы второго порядка:

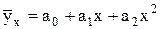, (7.2)

- параболы третьего порядка:

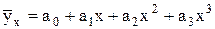, (7.3)

- показательной функции:

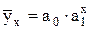, (7.4)

- полулогарифмической функции:

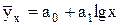, (7.5)

где 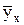- теоретические значения результативного признака;

а₀, а₁, а₂, а₃ - параметры уравнения регрессии;

х - эмпирические (реальные) значения факторного признака.

Для расчета параметров уравнения регрессии используют метод наименьших квадратов:

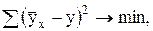(7.6)

где у - реальные значения результативного признака.

Базируясь на методе наименьших квадратов, можно составить следующие системы нормальных уравнений для расчета параметров а₀, а₁ и т.д.:

а) для уравнения прямой

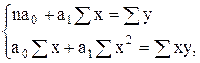(7.7)

б) для уравнения параболы второго порядка

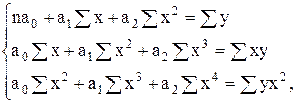(7.8)

в) для показательной функции

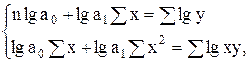(7.9)

г) для полулогарифмической функции

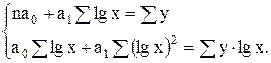(7.10)

Для определения параметров уравнений может использоваться либо способ совместного решения уравнений, либо способ определителей.

По способу определителей параметры уравнения прямой находятся следующим образом:

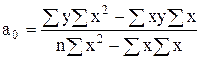(7.11)

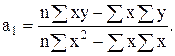(7.12)

Параметры уравнения показательной функции:

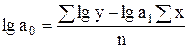(7.13)

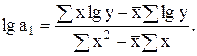(7.14)

Параметры уравнения полулогарифмической функции по методу определителей равны:

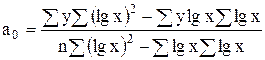(7.15)

(7.16)

Выбор уравнения, наиболее точно описывающего связь между факторным и результативным признаками, осуществляется при помощи остаточной дисперсии 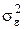(формула (7.25)). Наиболее точным считается то уравнение, у которого остаточная дисперсия имеет наименьшее значение.

Для определения тесноты связи используются различные показатели, как параметрические, так и непараметрические: коэффициент линейной корреляции, индекс корреляции (корреляционное отношение), коэффициент Фехнера, коэффициент корреляции рангов Спирмэна, коэффициенты ассоциации и контингенции, коэффициент взаимной сопряженности Чупрова и т.д.

Коэффициент корреляции используется только при линейной форме связи и рассчитывается по формулам:

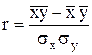(7.18)

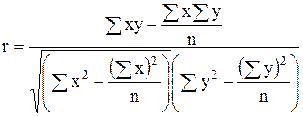. (7.19)

Индекс корреляции (корреляционное отношение) используется для линейной и нелинейной форм связи. Он находится как отношение:

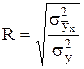, (7.20)

где 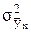- факторная дисперсия, обусловленная изменением результативного признака у только под воздействием изменения факторного признака х. Рассчитывается по формуле:

, (7.21)

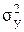- общая дисперсия результативного признака у, обусловленная воздействием всех факторов, а не только фактора х.

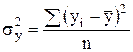, (7.22)

где 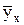- теоретические значения результативного признака, рассчитанные на основе уравнения регрессии;

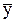- среднее значение результативного признака;

n - количество единиц в совокупности;

у_i - реальные значения результативного признака.

Коэффициент линейной корреляции "r" может принимать значения от -1 до 1. Отрицательное значение свидетельствует о наличии обратной связи между признаками х и у.

Индекс корреляции принимает значения от 0 до 1.

Если показатели тесноты связи будут равны 0, значит связь между х и у отсутствует.

Сила связи находится на основании показателей тесноты связи по шкале Чеддока.

Таблица 7.1