| §1 Теория графов
|
| 1. Определение графа
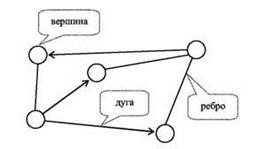
| Графом называется совокупность двух множеств: множества точек V и множество линий Е - подмножество VxV. Ясно, что Е={(vi,vj)| vi,vj ÎV}.
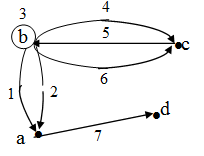
Множество V- множество вершин графа, Е – множество ребер. Обозначение: G=(V,E).
 Граф есть упорядоченная пара
Граф есть упорядоченная пара 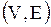 , где , где 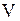 - непустое множество, называемое множеством вершин; - непустое множество, называемое множеством вершин; 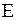 - бинарное отношение на - бинарное отношение на 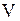 . Если . Если 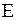 - неупорядоченное бинарное отношение на - неупорядоченное бинарное отношение на 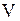 (т.е. (т.е. 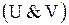 в в 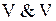 , то , то 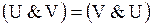 ), то ), то 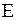 - множество ребер, и граф является неориентированным.
Ориентированный граф есть упорядоченная пара - множество ребер, и граф является неориентированным.
Ориентированный граф есть упорядоченная пара 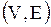 , где , где 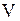 - множество вершин, а - множество вершин, а 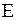 - упорядоченное отношение на - упорядоченное отношение на 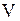 (т.е. (т.е. 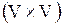 ). В этом случае ). В этом случае 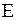 называется множеством дуг. Первая и вторая вершины дуги называется соответственно начальной и конечной вершинами. называется множеством дуг. Первая и вторая вершины дуги называется соответственно начальной и конечной вершинами.
|
| 2. Отношение инцидентности
| Между множествами V и Е устанавливается отношение инцидентности: двум элементам из множества V ставится в соответствие один элемент из множества Е.
|
| 3. Смежные вершины
| Два ребра, инцидентные одной вершине, называются смежными.
Если два смежные различных ребра инциденты одной и той же вершине, то они называются смежными.
Смешные вершины. Если две вершины инциденты одному ребру, то они называются смежными.
| Задача.
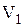 , , 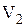 - смежные вершины; - смежные вершины; 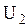 , , 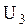 - не являются смежными; ребра - не являются смежными; ребра 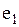 и и 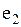 смежные ребра, а смежные ребра, а 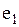 и и 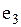 нет. нет.
|
| 4. Петля
| Если ребро инцидентно только одной вершине, то это петля.
Ребро, инцидентное только одной вершине, называется петлей.
|
| 5. Кратные ребра
| Два ребра, инцидентные одной паре вершин, называются кратными
Кратность пары вершин называется число соединяющих их ребер.
|
| 6. Безреберный граф
| Если множество Е пустое, то граф называется пустым (безреберным), все его вершины голые.
|
| 7. Полный граф
| Если все вершины графа попарно смежны, то граф полный.
|
| 8. Дополнительный граф
| Граф, дополняющий данный граф до полного, называется дополнительным.
|
| 9. Ориентированный (орграф), неориентированный граф
| Если ребра имеют направления, то граф ориентированный или орграф, иначе граф неориентированный.
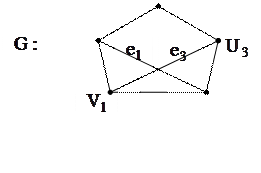
Геометрическая (графическая) интерпретация графа G=(V,E), где множество вершин V={a,b,c,d,e}, а множество ребер E={(a,c),(a,d),(b,d),(c,d)}, приведена на рисунке
 Неориентированный конечный граф.
Неориентированный конечный граф.
|
| 10. Изоморфные графы
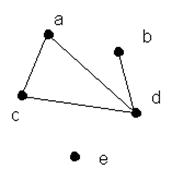
| Графы, отличающиеся только нумерацией вершин, но сохраняющие при этом множества V и E и соответственные инцидентности, называются изоморфными.
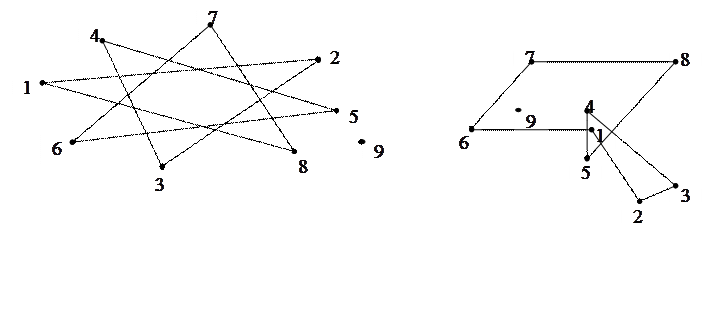 Графы изоморфны
Задача.
Изоморфны ли пары графов?
а)
Графы изоморфны
Задача.
Изоморфны ли пары графов?
а) 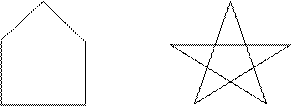 а) Изоморфны. Каждый из них состоит из одного простого цикла длины 5.
б)
а) Изоморфны. Каждый из них состоит из одного простого цикла длины 5.
б) 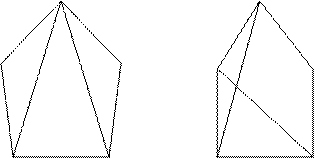 б) Неизоморфны. У одного есть вершина степени 4, а у второго нет.
г)
б) Неизоморфны. У одного есть вершина степени 4, а у второго нет.
г)  г) Несмотря на полное совпадение наборов степеней вершин графы неизоморфны: в одном их них есть мост – ребро при удалении которого он теряется связность, а в другом моста нет.
г) Несмотря на полное совпадение наборов степеней вершин графы неизоморфны: в одном их них есть мост – ребро при удалении которого он теряется связность, а в другом моста нет.
|
| 11. Мультиграф. Псевдограф
| Если у графа  имеется несколько дуг, исходящих из вершины имеется несколько дуг, исходящих из вершины  и заходящих в вершину и заходящих в вершину 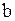 , то такие дуги называются кратными, а сам граф называется мультиграфом.
Псевдограф − граф, в котором есть петли и/или кратные ребра.
Мультиграф − псевдограф без петель. , то такие дуги называются кратными, а сам граф называется мультиграфом.
Псевдограф − граф, в котором есть петли и/или кратные ребра.
Мультиграф − псевдограф без петель.
| 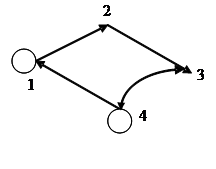 Задача.
На рисунке изображен мультиграф. Сколько исходящих дуг имеет вершина 4?
Решение.
Запишем вначале все дуги (исходящие и входящие), связанные с точкой 4.
Это дуги: (4; 1); (4; 3); (4; 4) и (3; 4). Исходящими из точки 4 являются первые три дуги. Последняя дуга (3; 4) – это входящая дуга в точку 4.
Ответ. 3. Задача.
На рисунке изображен мультиграф. Сколько исходящих дуг имеет вершина 4?
Решение.
Запишем вначале все дуги (исходящие и входящие), связанные с точкой 4.
Это дуги: (4; 1); (4; 3); (4; 4) и (3; 4). Исходящими из точки 4 являются первые три дуги. Последняя дуга (3; 4) – это входящая дуга в точку 4.
Ответ. 3.
|
| 12. Степень (валентность вершин)
| Степенью (или валентностью) вершины называется суммарное количество входящих в эту вершину и выходящих из нее дуг.
Если вершина изолированная, то ее степень равна нулю. Если вершина концевая, то ее степень равна единице.
Степенью (валентностью) вершины называется число инцидентных ей ребер.
|
| 13. Маршрут графа. Цепь/цикл графа
| В неориентированном (ориентированном) графе последовательность из 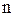 ребер (дуг) ребер (дуг) 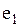 , , 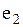 , … , … 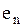 называется маршрутом (ориентированным маршрутом) длины называется маршрутом (ориентированным маршрутом) длины 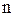 , если существует соответствующая последовательность из , если существует соответствующая последовательность из 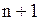 (не обязательно различных вершин) (не обязательно различных вершин) 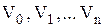 , таких, что , таких, что 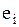 инциденто инциденто 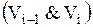 , , 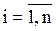 .
Маршрут (ориентированный маршрут) называется замкнутым (незамкнутым), если .
Маршрут (ориентированный маршрут) называется замкнутым (незамкнутым), если 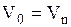 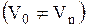 . Если . Если 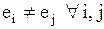 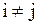 , то маршрут называется цепью (путем).
Если , то маршрут называется цепью (путем).
Если 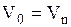 , то цепь (путь) называется циклом (контуром). Если вершины различны, получаем простую цепь. , то цепь (путь) называется циклом (контуром). Если вершины различны, получаем простую цепь.
|
| 14. Связный граф
| Граф называется связным, если каждая пара вершин может быть соединена цепью.
|
| 15. Компоненты графа
| Граф, который не является связным, может быть разбит на конечное число связных подграфов, называемых компонентами или частями.
|
| 16. Связность графа
| Связностью графа называется наименьшее число вершин, удаление которых делает исходный граф несвязным.
|
| 17. Разрез графа
| Разрезом графа называется минимальное множество ребер, удаление которых увеличивает число компонент.
|
| 18. Полный граф
| Граф называется полным, если каждая вершина соединена ребром с каждой из всех других вершин.
|
  На рисунке
На рисунке 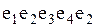 - маршрут; - маршрут; 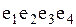 - цепь; - цепь; 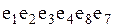 - цикл; - цикл; 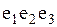 - простая цепь; - простая цепь; 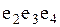 - простой цикл; - простой цикл; 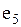 - разрез. - разрез.
|
| 19. Двудольный граф
| Граф называется двудольным, если его вершины могут быть разбиты на два таких множества, что каждое ребро соединяет вершину одного множества с вершиной другого.
|
| 20. Регулярный граф
| Связный граф называется регулярным, если все его вершины имеют одинаковую степень.
|
| 21. Эйлеров путь. Критерий Эйлера
| Эйлеровым путем в графе G называется такой путь, в котором каждое из ребер встречается только один раз. Эйлер показал, что такой путь существует тогда и только тогда, когда граф содержит не более двух вершин нечетной степени и является связным. Эйлеров цикл существует тогда и только тогда, когда в нем все вершины четные.
ТеоремаЭйлера. В любом конечном графе сумма степеней вершин равна удвоенному числу его ребер.
|
| 22. Матрица смежности
| Матрица смежности
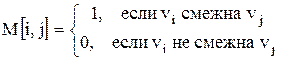 данная матрица симметрична относительно главной диагонали, а главная диагональ состоит из нулей, за исключением петель.
данная матрица симметрична относительно главной диагонали, а главная диагональ состоит из нулей, за исключением петель.
|  Задача.
Составить матрицу смежности для графа, изображенного на рисунке.
Решение.
Граф, изображенный на рисунке Задача.
Составить матрицу смежности для графа, изображенного на рисунке.
Решение.
Граф, изображенный на рисунке 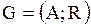 состоит из трех состоит из трех 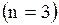 вершин вершин 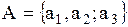 . И двух дуг . И двух дуг 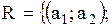 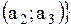 . Значит матрица смежности . Значит матрица смежности 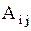 для нашего графа будет размером для нашего графа будет размером 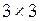 : :
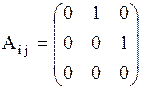 .
Поясним, как получена первая строка матрицы. Первая строка .
Поясним, как получена первая строка матрицы. Первая строка 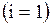 показывает связь точки показывает связь точки 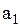 с остальными точками: дуги с остальными точками: дуги 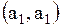 , то есть петли, нет, значит 0; дуга , то есть петли, нет, значит 0; дуга 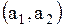 есть, значит 1; дуги есть, значит 1; дуги 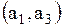 нет, значит – 0. Поясним вторую строку нет, значит – 0. Поясним вторую строку 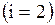 . Она показывает связь точки . Она показывает связь точки 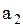 с остальными точками: дуги с остальными точками: дуги 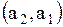 нет, значит – 0, дуги нет, значит – 0, дуги 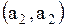 , то есть петли, нет, значит – 0; дуга , то есть петли, нет, значит – 0; дуга 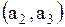 есть, значит 1. Третья строка полностью состоит из нулей, так как из точки есть, значит 1. Третья строка полностью состоит из нулей, так как из точки 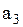 к остальным точкам нет связи, значит нет дуг: к остальным точкам нет связи, значит нет дуг: 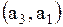 ; ; 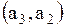 ; ; 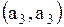 .
Ответ. .
Ответ. 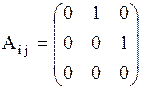 . .
|
| 23. Матрица инциндентности
| Матрица инцидентности
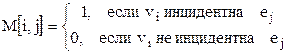 в случае неориентированного графа в случае неориентированного графа
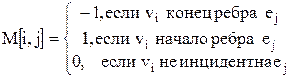 в случае ориентированного графа в случае ориентированного графа
| Задача.
Записать матрицу инцидентности для мультиграфа 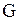 , изображенного на рисунке. , изображенного на рисунке.
 Решение.
Мультиграф, изображенный на рисунке Решение.
Мультиграф, изображенный на рисунке 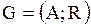 - орентирован, состоит из четырех - орентирован, состоит из четырех 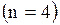 вершин вершин 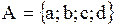 и семи и семи 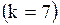 дуг (на рисунке дуги дополнительно обозначены цифрами). Значит матрица будет размером дуг (на рисунке дуги дополнительно обозначены цифрами). Значит матрица будет размером 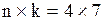 , то есть четыре строки и семь столбцов: , то есть четыре строки и семь столбцов:
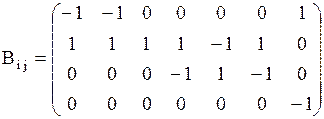 .
Поясним первую строку. Она показывает расположение всех семи дуг по отношении к точке .
Поясним первую строку. Она показывает расположение всех семи дуг по отношении к точке 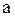 :
дуга 1 в точку :
дуга 1 в точку 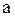 входит, значит ставим (– 1);
дуга 2 в точку входит, значит ставим (– 1);
дуга 2 в точку 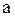 входит, значит ставим (– 1);
дуги 3, 4, 5, 6 в точку входит, значит ставим (– 1);
дуги 3, 4, 5, 6 в точку 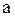 не входят и не выходят, поэтому в первой строке на месте 3, 4, 5,6 стоят нули;
дуга 7 из точки не входят и не выходят, поэтому в первой строке на месте 3, 4, 5,6 стоят нули;
дуга 7 из точки 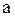 выходит, поэтому в первой строке на седьмом месте стоит единица.
Поясним вторую строку матрицы. Она показывает расположение всех дуг по отношению к точке выходит, поэтому в первой строке на седьмом месте стоит единица.
Поясним вторую строку матрицы. Она показывает расположение всех дуг по отношению к точке 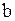 : дуги 1, 2, 3, 4 и 6 выходят из точки : дуги 1, 2, 3, 4 и 6 выходят из точки 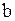 , поэтому во второй строке на первом, втором, третьем, четвертом и шестом местах стоят единицы. А вот дуга 5 в точку , поэтому во второй строке на первом, втором, третьем, четвертом и шестом местах стоят единицы. А вот дуга 5 в точку 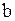 входит, поэтому на пятом месте стоит (– 1). Дуга 7 в точку входит, поэтому на пятом месте стоит (– 1). Дуга 7 в точку 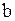 не входит и не выходит, поэтому на седьмом месте стоит 0.
Аналогично формируются третья строка (соответствующая точке не входит и не выходит, поэтому на седьмом месте стоит 0.
Аналогично формируются третья строка (соответствующая точке 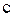 ) и четвертая строка (соответствующая точке ) и четвертая строка (соответствующая точке 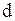 ). Предлагаем самостоятельно проанализировать эти строки. ). Предлагаем самостоятельно проанализировать эти строки.
|
| 24. Дерево
| В неориентированном графе связный подграф, не имеющий циклов называется деревом.
Если все вершины графа принадлежат дереву, то оно называется покрывающим.
Ориентированное дерево имеет корень в вершине 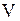 , если существует путь от , если существует путь от 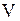 к каждой из других вершин. Ребра графа, принадлежащие покрывающему дереву, называются ветвями. Все остальные ребра называются хордами. к каждой из других вершин. Ребра графа, принадлежащие покрывающему дереву, называются ветвями. Все остальные ребра называются хордами.
|
|
| Матрица инциденций неориентированного графа обладает следующими очевидными свойствами:
1) в графе без петель каждый столбец этой матрицы имеет в точности две единицы, соответствующие паре вершин ребра;
2) если в графе имеются петли, то в столбцах, соответствующих петлям, имеется по одной единице, а в остальных – по две.
|
| | | | |

 Граф есть упорядоченная пара
Граф есть упорядоченная пара 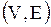 , где
, где 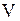 - непустое множество, называемое множеством вершин;
- непустое множество, называемое множеством вершин; 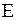 - бинарное отношение на
- бинарное отношение на 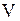 . Если
. Если 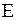 - неупорядоченное бинарное отношение на
- неупорядоченное бинарное отношение на 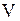 (т.е.
(т.е. 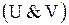 в
в 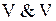 , то
, то 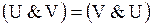 ), то
), то 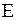 - множество ребер, и граф является неориентированным.
Ориентированный граф есть упорядоченная пара
- множество ребер, и граф является неориентированным.
Ориентированный граф есть упорядоченная пара 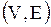 , где
, где 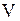 - множество вершин, а
- множество вершин, а 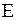 - упорядоченное отношение на
- упорядоченное отношение на 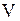 (т.е.
(т.е. 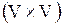 ). В этом случае
). В этом случае 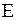 называется множеством дуг. Первая и вторая вершины дуги называется соответственно начальной и конечной вершинами.
называется множеством дуг. Первая и вторая вершины дуги называется соответственно начальной и конечной вершинами.
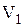 ,
, 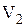 - смежные вершины;
- смежные вершины; 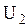 ,
, 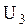 - не являются смежными; ребра
- не являются смежными; ребра 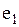 и
и 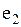 смежные ребра, а
смежные ребра, а 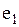 и
и 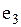 нет.
нет.

 Неориентированный конечный граф.
Неориентированный конечный граф.
 Графы изоморфны
Задача.
Изоморфны ли пары графов?
а)
Графы изоморфны
Задача.
Изоморфны ли пары графов?
а)  а) Изоморфны. Каждый из них состоит из одного простого цикла длины 5.
б)
а) Изоморфны. Каждый из них состоит из одного простого цикла длины 5.
б)  б) Неизоморфны. У одного есть вершина степени 4, а у второго нет.
г)
б) Неизоморфны. У одного есть вершина степени 4, а у второго нет.
г)  г) Несмотря на полное совпадение наборов степеней вершин графы неизоморфны: в одном их них есть мост – ребро при удалении которого он теряется связность, а в другом моста нет.
г) Несмотря на полное совпадение наборов степеней вершин графы неизоморфны: в одном их них есть мост – ребро при удалении которого он теряется связность, а в другом моста нет.
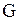 имеется несколько дуг, исходящих из вершины
имеется несколько дуг, исходящих из вершины 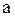 и заходящих в вершину
и заходящих в вершину 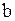 , то такие дуги называются кратными, а сам граф называется мультиграфом.
Псевдограф − граф, в котором есть петли и/или кратные ребра.
Мультиграф − псевдограф без петель.
, то такие дуги называются кратными, а сам граф называется мультиграфом.
Псевдограф − граф, в котором есть петли и/или кратные ребра.
Мультиграф − псевдограф без петель.
 Задача.
На рисунке изображен мультиграф. Сколько исходящих дуг имеет вершина 4?
Решение.
Запишем вначале все дуги (исходящие и входящие), связанные с точкой 4.
Это дуги: (4; 1); (4; 3); (4; 4) и (3; 4). Исходящими из точки 4 являются первые три дуги. Последняя дуга (3; 4) – это входящая дуга в точку 4.
Ответ. 3.
Задача.
На рисунке изображен мультиграф. Сколько исходящих дуг имеет вершина 4?
Решение.
Запишем вначале все дуги (исходящие и входящие), связанные с точкой 4.
Это дуги: (4; 1); (4; 3); (4; 4) и (3; 4). Исходящими из точки 4 являются первые три дуги. Последняя дуга (3; 4) – это входящая дуга в точку 4.
Ответ. 3.
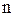 ребер (дуг)
ребер (дуг) 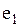 ,
, 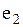 , …
, … 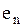 называется маршрутом (ориентированным маршрутом) длины
называется маршрутом (ориентированным маршрутом) длины 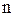 , если существует соответствующая последовательность из
, если существует соответствующая последовательность из 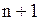 (не обязательно различных вершин)
(не обязательно различных вершин) 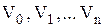 , таких, что
, таких, что 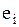 инциденто
инциденто 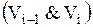 ,
, 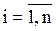 .
Маршрут (ориентированный маршрут) называется замкнутым (незамкнутым), если
.
Маршрут (ориентированный маршрут) называется замкнутым (незамкнутым), если 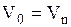
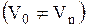 . Если
. Если 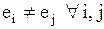
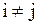 , то маршрут называется цепью (путем).
Если
, то маршрут называется цепью (путем).
Если 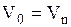 , то цепь (путь) называется циклом (контуром). Если вершины различны, получаем простую цепь.
, то цепь (путь) называется циклом (контуром). Если вершины различны, получаем простую цепь.

 На рисунке
На рисунке 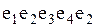 - маршрут;
- маршрут; 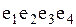 - цепь;
- цепь; 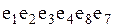 - цикл;
- цикл; 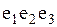 - простая цепь;
- простая цепь; 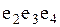 - простой цикл;
- простой цикл; 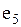 - разрез.
- разрез.
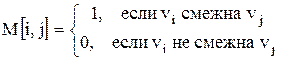 данная матрица симметрична относительно главной диагонали, а главная диагональ состоит из нулей, за исключением петель.
данная матрица симметрична относительно главной диагонали, а главная диагональ состоит из нулей, за исключением петель.
 Задача.
Составить матрицу смежности для графа, изображенного на рисунке.
Решение.
Граф, изображенный на рисунке
Задача.
Составить матрицу смежности для графа, изображенного на рисунке.
Решение.
Граф, изображенный на рисунке 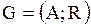 состоит из трех
состоит из трех 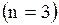 вершин
вершин 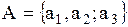 . И двух дуг
. И двух дуг 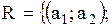
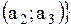 . Значит матрица смежности
. Значит матрица смежности 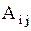 для нашего графа будет размером
для нашего графа будет размером 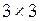 :
:
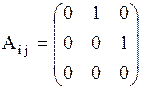 .
Поясним, как получена первая строка матрицы. Первая строка
.
Поясним, как получена первая строка матрицы. Первая строка 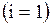 показывает связь точки
показывает связь точки 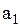 с остальными точками: дуги
с остальными точками: дуги 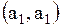 , то есть петли, нет, значит 0; дуга
, то есть петли, нет, значит 0; дуга 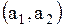 есть, значит 1; дуги
есть, значит 1; дуги 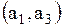 нет, значит – 0. Поясним вторую строку
нет, значит – 0. Поясним вторую строку 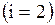 . Она показывает связь точки
. Она показывает связь точки 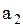 с остальными точками: дуги
с остальными точками: дуги 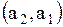 нет, значит – 0, дуги
нет, значит – 0, дуги 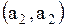 , то есть петли, нет, значит – 0; дуга
, то есть петли, нет, значит – 0; дуга 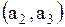 есть, значит 1. Третья строка полностью состоит из нулей, так как из точки
есть, значит 1. Третья строка полностью состоит из нулей, так как из точки 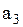 к остальным точкам нет связи, значит нет дуг:
к остальным точкам нет связи, значит нет дуг: 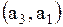 ;
; 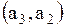 ;
; 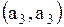 .
Ответ.
.
Ответ. 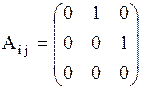 .
.
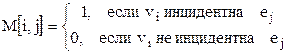 в случае неориентированного графа
в случае неориентированного графа
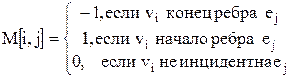 в случае ориентированного графа
в случае ориентированного графа
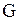 , изображенного на рисунке.
, изображенного на рисунке.
 Решение.
Мультиграф, изображенный на рисунке
Решение.
Мультиграф, изображенный на рисунке 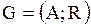 - орентирован, состоит из четырех
- орентирован, состоит из четырех 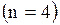 вершин
вершин 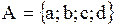 и семи
и семи 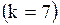 дуг (на рисунке дуги дополнительно обозначены цифрами). Значит матрица будет размером
дуг (на рисунке дуги дополнительно обозначены цифрами). Значит матрица будет размером 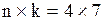 , то есть четыре строки и семь столбцов:
, то есть четыре строки и семь столбцов:
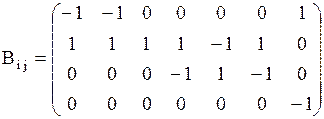 .
Поясним первую строку. Она показывает расположение всех семи дуг по отношении к точке
.
Поясним первую строку. Она показывает расположение всех семи дуг по отношении к точке 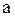 :
дуга 1 в точку
:
дуга 1 в точку 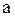 входит, значит ставим (– 1);
дуга 2 в точку
входит, значит ставим (– 1);
дуга 2 в точку 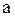 входит, значит ставим (– 1);
дуги 3, 4, 5, 6 в точку
входит, значит ставим (– 1);
дуги 3, 4, 5, 6 в точку 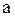 не входят и не выходят, поэтому в первой строке на месте 3, 4, 5,6 стоят нули;
дуга 7 из точки
не входят и не выходят, поэтому в первой строке на месте 3, 4, 5,6 стоят нули;
дуга 7 из точки 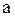 выходит, поэтому в первой строке на седьмом месте стоит единица.
Поясним вторую строку матрицы. Она показывает расположение всех дуг по отношению к точке
выходит, поэтому в первой строке на седьмом месте стоит единица.
Поясним вторую строку матрицы. Она показывает расположение всех дуг по отношению к точке 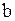 : дуги 1, 2, 3, 4 и 6 выходят из точки
: дуги 1, 2, 3, 4 и 6 выходят из точки 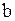 , поэтому во второй строке на первом, втором, третьем, четвертом и шестом местах стоят единицы. А вот дуга 5 в точку
, поэтому во второй строке на первом, втором, третьем, четвертом и шестом местах стоят единицы. А вот дуга 5 в точку 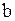 входит, поэтому на пятом месте стоит (– 1). Дуга 7 в точку
входит, поэтому на пятом месте стоит (– 1). Дуга 7 в точку 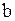 не входит и не выходит, поэтому на седьмом месте стоит 0.
Аналогично формируются третья строка (соответствующая точке
не входит и не выходит, поэтому на седьмом месте стоит 0.
Аналогично формируются третья строка (соответствующая точке 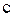 ) и четвертая строка (соответствующая точке
) и четвертая строка (соответствующая точке 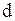 ). Предлагаем самостоятельно проанализировать эти строки.
). Предлагаем самостоятельно проанализировать эти строки.
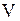 , если существует путь от
, если существует путь от 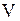 к каждой из других вершин. Ребра графа, принадлежащие покрывающему дереву, называются ветвями. Все остальные ребра называются хордами.
к каждой из других вершин. Ребра графа, принадлежащие покрывающему дереву, называются ветвями. Все остальные ребра называются хордами.