 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ортонормированный базис евклидова пространства
|
|
Азн. 13.8. Базіс 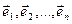 (2) n-мерного евклидового пространства называется ортонормированным, когда он ортогональный и все его векторы нормированные, то есть
(2) n-мерного евклидового пространства называется ортонормированным, когда он ортогональный и все его векторы нормированные, то есть 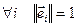 .
.
Тэарэма 13.9. Базис (2) евклидового пространства ε n является ортонормированным тогда и только тогда, когда ортогональное достояние произвольных векторов 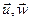 , которые в этом базисе имеют координаты
, которые в этом базисе имеют координаты 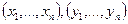 , грядет равный:
, грядет равный: 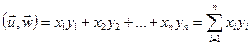 (3). Доказ: Если
(3). Доказ: Если  - ортонормированный, тогда по 14.2
- ортонормированный, тогда по 14.2 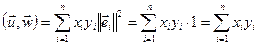 . Пусть правдиво (3). Тогда поскольку
. Пусть правдиво (3). Тогда поскольку  в базисе (2) мои координаты (1,0,0,...,0) получаем что:
в базисе (2) мои координаты (1,0,0,...,0) получаем что: 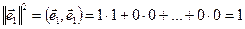 .
.
Откуда 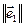 =1. Аналогично
=1. Аналогично 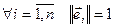 . Когда
. Когда 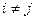 з (3) следует, что
з (3) следует, что 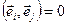 , то (2) – ортонормированный базис.■
, то (2) – ортонормированный базис.■
Тэарэма 13.10. В каждой конечномерном евклидовом пространстве существует ортонормированный базис.
Доказ: В евклидовом пространстве εn существует базис 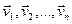 . Идея доказательства в том, чтобы построить постепенно посредством этого базиса ортогональный базис
. Идея доказательства в том, чтобы построить постепенно посредством этого базиса ортогональный базис 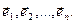 Возьмем
Возьмем 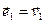 . Очевидно, что
. Очевидно, что 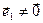 . Будем искать
. Будем искать 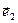 в виде
в виде 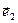 =
= 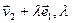 Î R. Из условия ортогональности следует, что 0=(
Î R. Из условия ортогональности следует, что 0=(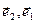 )=(
)=(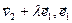 )=
)= 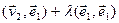 . Но
. Но 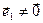 , последнее равенство эквивалентно тому, что
, последнее равенство эквивалентно тому, что 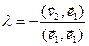 . Таким образом, нашли
. Таким образом, нашли 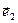 такой, что (
такой, что (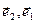 )=0. Заметим, что векторы
)=0. Заметим, что векторы 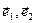 получили из векторов
получили из векторов 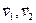 посредством элементарных преобразований. По 14.5 ранги систем векторов
посредством элементарных преобразований. По 14.5 ранги систем векторов 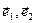 і
і 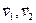 равные, то
равные, то 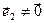 . Когда построили систему ненулевых попарно ортогональных векторов
. Когда построили систему ненулевых попарно ортогональных векторов
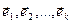 і
і 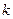 <
< 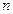 , тогда вектор
, тогда вектор 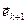 будем искать в виде:
будем искать в виде: 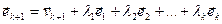 . Рассмотрим
. Рассмотрим 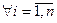 (
(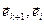 )=(
)=(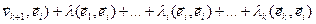 . Условие попарной взаимоортогональности векторов
. Условие попарной взаимоортогональности векторов 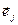 ,
,  эквивалентная тому, что 0=(
эквивалентная тому, что 0=(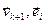 )+
)+ 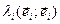 , поскольку
, поскольку 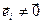 , последнее равенство эквивалентно тому, что
, последнее равенство эквивалентно тому, что 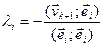 Таким образом, получаем систему попарно ортогональных векторов
Таким образом, получаем систему попарно ортогональных векторов 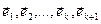 . Остается заметить, что последняя система получается из системы
. Остается заметить, что последняя система получается из системы 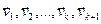 посредством элементарных преобразований, значиться их ранги равные
посредством элементарных преобразований, значиться их ранги равные 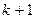 , і
, і 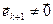 . Таким путям мы получим систему попарно ортогональных векторов
. Таким путям мы получим систему попарно ортогональных векторов 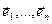 , ранг какой равный n, из чего следует, что эти векторы образовывают ортогональный базис пространства
, ранг какой равный n, из чего следует, что эти векторы образовывают ортогональный базис пространства 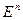 . Исходя из базиса
. Исходя из базиса 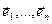 , рассмотрим векторы
, рассмотрим векторы 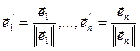 . То
. То 
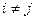
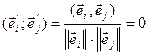 . Па 12.9
. Па 12.9 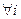
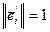 , значит векторы
, значит векторы 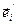 образовывают ортонормированный базис.■
образовывают ортонормированный базис.■
Св-во 13.11. Когда 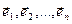 - ортонормированный базис ε n,
- ортонормированный базис ε n, 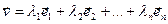 , то
, то 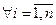
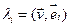 . Доказ:
. Доказ: 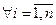
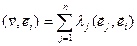 . Из условия ортонормируемости следует, что
. Из условия ортонормируемости следует, что 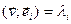 .■
.■
Св-во 13.12. Когда 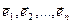 - ортонормированный базис ε n, векторы
- ортонормированный базис ε n, векторы 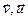 имеют в этом базисе столбцы координат X и Y соответственно, тогда
имеют в этом базисе столбцы координат X и Y соответственно, тогда 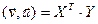 . Доказ.
. Доказ. 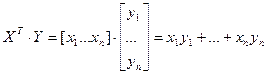 , что по 14.4 ровно
, что по 14.4 ровно 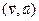 . ■
. ■
Дата публикования: 2014-11-04; Прочитано: 533 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
