Подпространства. Свойства. Линейная оболочка системы векторов

Опр. 13.1. Пусть V линейное пространство над полем Р. Непустое подмножество U V называют подпространством пространства V, когда U является линейным пространством относительно операций, какие указанный в V.

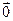
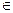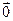
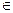Ул. 7.6. Когда U и W подпространства пространства V, тогда U ∩ W - подпространство пространства V. Доказательство.1. Так как U і W, 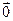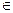U ∩ W, значиться U ∩ W ≠Ø.

2. Когда 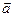и и 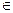U ∩ W, тогда по 7.2.2 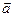+ 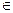U и 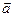+ 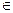W, откуда 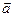+ 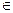U ∩ W.

3. Когда 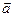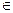U ∩ W і λ 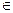Р, тогда по 7.2.3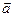 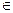λ U и λ 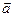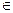W, значиться λ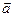 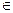U ∩ W ■

Итог.7.7. Когда { U_i }_{( i 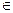І)} линейные подпространства V, тогда U = ∩ U_i - подпространство в V.

Доказательство. Аналогично 7.6. ■

Ул. 7.3. Когда U подпространство линейного пространства V и dim V <∞, тогда dim U ≤ dim V. Доказательство. Когда U ={ 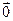} утверждение очевидно. Когда U ≠{ 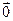}, тогда dim U =k і u₁,…, u_k базис U. Тогда, по 5.4, k≤ dim V. ■

Ул. 7.4. Когда U подпространство в V, dim V <∞ и dim U = dim V, тогдп U = V. Доказательство. Пусть 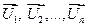- базис U, тогда это n линейно независимых векторов n-мерного пространства V. Значит это базис V. ■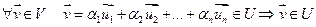

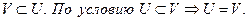Ул. 7.5. Пусть размерность dim V <∞ и 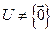в V, тогда произвольный базис подпространства U в V можно дополнить до базиса пространства V. Доказательство. Следует из теоремы (Любая линейнозависимая подсистема системы 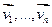содержится в ее МЛНП, в частности, любой ненулевой вектор из 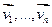содержится в МЛНП.) и определения базиса. ■

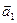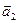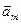
Азн. 7.8. V- линейное пространство над Р, , ,..., 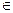V. Через L( 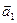, ,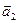..., 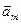)= { λ ₁ 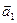+…+ λ _n 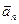| λ _i 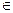P} будем обозначать линейную оболочку множества векторов { 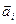}, i = .

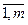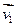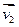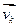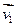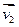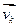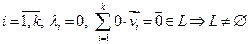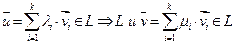
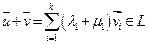
Св-во 7.7. L(, ,..., ) – подпространство V (натянутый на вектор , ,..., ). Доказательство: . Пусть 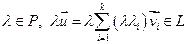, тоэто подпространство. ■

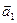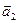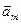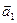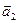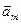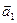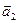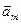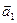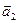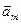Ул. 7.9. L( , ,..., ) - наименьшая из подпространств V, что удерживает { , ,..., }. [ Наименьшая в том смысле, что когда U подпространство в V и { , ,..., } U, тогда L( , ,..., ) U ].
Доказательство: Пусть U удовлетворяет условию свойства, тогда ■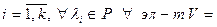

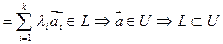Св-во 7.10. Пусть 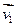, ,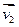..., 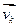- система векторов пространства V, содержащая хотя бы 1 ненулевой вектор, тогда если ранг этой системы векторов = r, то 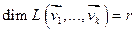и для любой МЛНП этой системы векторов является базисом 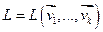. Доказательство: Пусть 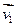, ,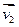..., 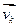- МЛНП, тогда лин.завис. Любой вектор системы выражается через МЛНП, а МЛНП полна в L, значит МЛНП – базис в L. ■