Случайные величины 6 страница

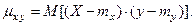(1)

Замечание 1. Нетрудно убедиться, что корреляционный мо -мент можно записать в виде:

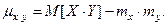
Замечание 2. Корреляционный момент двух независимых случайных величин равен нулю.

Это следует из условия независимости случайных величин.

Замечание 3. Для корреляционного момента случайных ве – личин и выполняется неравенство

Определение. Коэффициентом корреляции 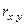случайных величин и называют отношение корреляционного мо -мента к произведению средних квадратических отклонений этих величин, т.е.

(2)

Если случайные величины независимы, то их корреляци- онный смомент равен нулю и, соответственно равен нулю их коэффициент корреляции.

Учитывая замечание 3, получаем основное свойство коэффициента корреляции:

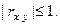(3)

Пример 7. Рассмотрим случай системы дискретных случай- ных величин, распределение которых забано таблицей:

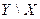
-1	0,12	0,14	0,11	0,07
	0,12	0,14	0,07	0,04
	0,05	0,07	0,04	0,03

Найти математические ожтдания и дисперсии составляющих и найти для них коэффициент корреляции .

Найдём одномерные законы распределения составляющих

и их числовые характеристики.

Для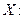

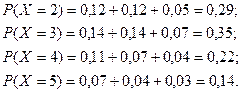
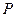
	0,29	0,35	0,22	0,14

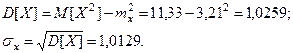
Для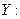

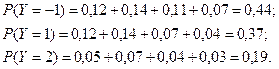
	-1
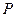
	0,44	0,37	0,19

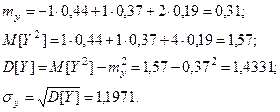
Математическое ожидание произведения:

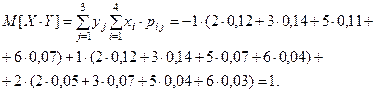Тогда корреляционный момент равен:

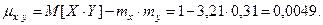
И окончательно, коэффициент корреляции равен:

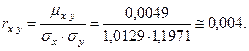
Это означает, что случайные величины и имеют очень слабую зависимость.

Рассмотрим аналогичную задачу для случая непрерывных случайных величин.

Пример 8. Пусть система случайных величин 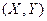подчинена закону распределения с плотностью:

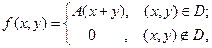
где область . Найти значение параметра 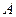, числовые характеристики случайных величин и и их коэффициент корреляции .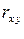

Область 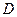- это треугольник:

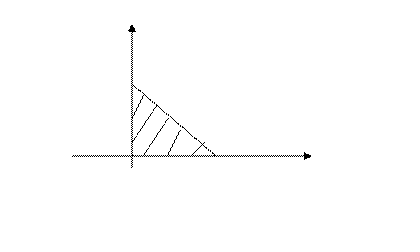
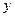
0 2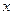

Сначала найдём значение параметра 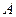, учитывая ос -новное условие плотности распределения:

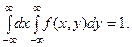
В нашем случае,

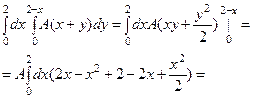
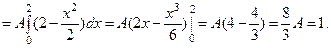
Отсюда, 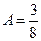и плотность распределения имеет вид:

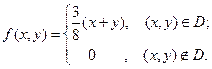
Найдём числовые характеристики составляющих.

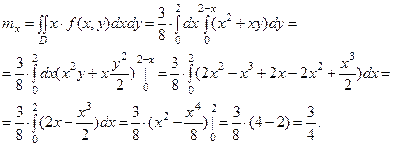
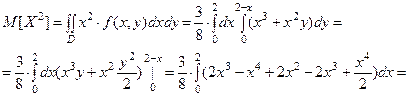
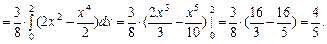
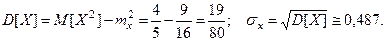
Так как функция 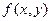и область 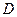симметричны относи -тельно 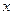и 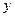, то числовые характеричтики случайных вели -чин и совпадают, т.е.

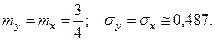
Математическое ожидание произведения случайных величин

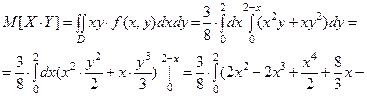
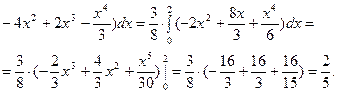Корреляционный момент равен:

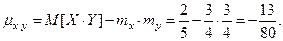
И окончательно,

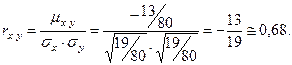
8.6. Коррелированность и зависимость случайных

величин

Определение. Две случайные величины и называют коррелированными, если их корреляционный момент (или, что равносильно, коэффициент корреляции) отличен от нуля.

Коррелированные величины являются зависимыми. Обрат -ное предположение не всегда имеет место, т.е. зависимые случайные величины могут быть и коррелированными и не коррелированными. Если случайные величины независимые, то они обязательно некоррелированы.

Убедимся на примере, что две зависимые величины могут быть некоррелированными.

Пример. Пусть двумерная случайная величина 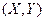за – дана плотностью распределения:

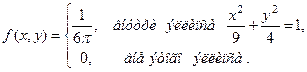
Доказать, что и - некоррелированные величины.

Плотности распределения составляющих, как нетрудно убе -диться внутри заданного эллипса задаются соответствующими формулами 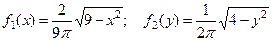и равны нулю вне эллипса.

Так как 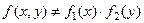, то и - зависимые случайные величины.

Так как функция 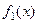симметрична относительно оси Оу, то 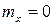, аналогично, 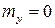, ввиду симметрии 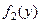относительно оси Ох (чётные функции).

так как равен нулю внутренний интеграл (интеграл от нечётной функции равен чётной функции, а пределы интегрирования симметричны). Тогда

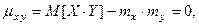т.е. данные зависимые случайные величины не являются кор- релированными.

Замечание 1. Для нормально распределённых составляющих двумерной случайной величины понятия некоррелированности и независимости равносильны.

Замечание 2. Если составляющие и связаны линей- ной зависимостью, т.е. 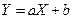, то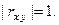

БИБЛИОГРАФИЧЕСКИЙ СПИСОК