 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Случайные величины 5 страница
|
|
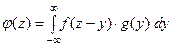 .
.
В частности, если 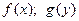 принимают только положи- тельные значения на промежутке
принимают только положи- тельные значения на промежутке  , то выполняютя сле- дующие формулы:
, то выполняютя сле- дующие формулы:

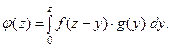
ПРИМЕР 2. Пусть независимые случайные величины  и
и  заданы своими плотностями распределения:
заданы своими плотностями распределения:
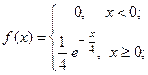
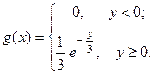
Найти закон распределения случайной величины 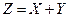 .
.
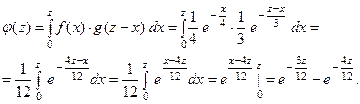
Таким образом,
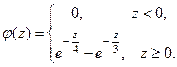
Легко проверить, что выполняется основное свойство плотнос -ти распределения, а именно,
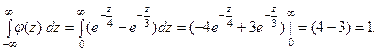
§ 8. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
8.1 Законы распределения системы случайных величин.
Все случайные величины, которые рассматричались до сих пор, определялись одним числом (одним аргументом) - одно -мерные случайные величины. Но, кроме них, можем рассмот- реть величины, которые зависят от двух, трёх и более аргу –ментов, так называемые, многомерные случайные величины, которые можно рассматривать как системы одномерных слу -чайных величин. Через 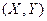 - обозначают двумерную слу- чайную величину, а каждую из величин
- обозначают двумерную слу- чайную величину, а каждую из величин  и
и  - называют составляющей (компонентой).
- называют составляющей (компонентой).
Двумерную случайную величину называют дискретной, если её составляющие - дискретные случайные величины.
Непрерывной называют двумерную случайную величину, сос- тавляющие которой - непрерывные случайные величины.
Законом распределения дискретной двумерной случайной величинв называют таблицу вида:

| 
| |||||
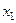
| 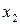
| 
| 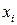
| 
| 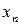
| |
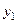
| 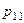 
| 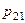
| 
| 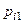
| 
| 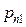
|

| 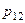
| 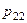
| 
| 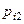
| 
| 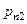
|

| 
| 
| 
| 
| 
| 
|
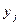
| 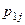
| 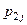
| 
| 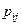
| 
| 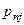
|

| 
| 
| 
| 
| 
| 
|
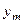
| 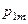
| 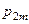
| 
| 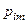
| 
| 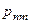
|
Так как события 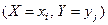 ,
, 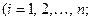
 образуют полную группу несовместных событий, то сумма всех вероятностей
образуют полную группу несовместных событий, то сумма всех вероятностей 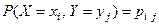 , стоящих в таблице, равна единице.
, стоящих в таблице, равна единице.
Зная закон распределения двумерной случайной величины, можно найти закон распределения каждой составляющей:
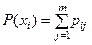 (сумма вероятностей в столбце таблицы);
(сумма вероятностей в столбце таблицы);
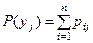 (сумма вероятностей в строке таблицы).
(сумма вероятностей в строке таблицы).
Пример 1. Дан закон распределения двумерной случайнойвеличины:
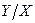
| |||
| -1 | 0,12 | 0,28 | 0,11 |
| 0,21 | 0,14 | 0,14 |
Составить законы распределения случайных величин  и
и  .
.
Случайная величина  имеет распределение:
имеет распределение:

| |||
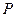
| 0,33 | 0,42 | 0,25 |
Для случайной величины  получаем ряд:
получаем ряд:

| -1 | |
| 0,51 | 0,49 |
Определение. Функцией распределения двумерной случайной величины называют функцию  , которая имеет смыс как для дискретных, так и для непрерыв- ных случайных величин. Геометрически это равество можно истолковать, как вероятность того, что случайная точка
, которая имеет смыс как для дискретных, так и для непрерыв- ных случайных величин. Геометрически это равество можно истолковать, как вероятность того, что случайная точка 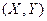 попадает в бесконечный квадрат с вершиной в точке
попадает в бесконечный квадрат с вершиной в точке 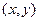 , расположенный левее и ниже этой вершины.
, расположенный левее и ниже этой вершины.
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ:
Свойство 1. 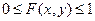 .
.
Свойство 2. Функция распределения - неубывающая функция по обоим аргументам, т.е.
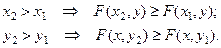
Свойство 3. Для всех 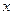 и
и 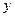 выполняются следующие соотношения:
выполняются следующие соотношения:
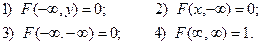
Свойство 4. Функции распределения составляющих можно найти из равенств:
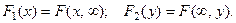
Определение. Плотностью совместного распределения ве- роятностей двумерной непрерывной случайной величины назы- вается вторая смешанная производная от фукнкции распреде –ления, т.е.
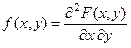 .
.
Пример 2. Дана функция распределения системы случайных величин 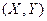 :
: 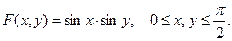 Найти её плотность распределения.
Найти её плотность распределения.
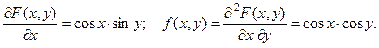
Пусть известна плотность распределения системы случай - ных величин 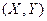 -
- 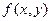 . Тогда функцию распределе -ния можно найти, используя равенство:
. Тогда функцию распределе -ния можно найти, используя равенство:
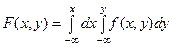 ,
,
Это непосредственно следует из определения плотности рас- пределения.
Вероятность попадания 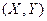 в область
в область 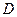 определя -ется равенством
определя -ется равенством
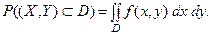
СВОЙСТВА ДВУМЕРНОЙ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ.
Свойство 1. Двумерная плотность распределения всегда по- ложительна: 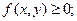
Свойство 2. Двойной несобственный интеграл с бесконеч - ными пределами интегрирования от плотности распределения равен единице
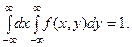
Если известна плотность совместного распределения веро- ятностей системы двух случайных величин, то можно найти плотности распределения каждой составляющей. 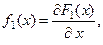 но
но 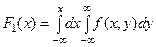 . Тогда
. Тогда
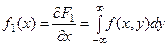 .
.
Аналогичным образом получаем
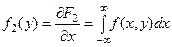 ,
,
где
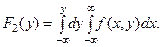
Пример 3. Пусть дана двумерная плотность распределения
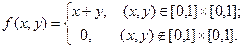
Найти плотности распределения случайных величин  и
и 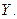
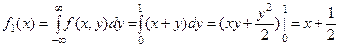
при 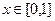 и равна нулю вне этого промежутка. Аналогично, ввиду симметрии функции
и равна нулю вне этого промежутка. Аналогично, ввиду симметрии функции 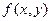 относительно
относительно 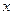 и
и 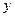 , получаем:
, получаем:
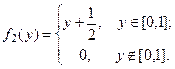
8.2 Условные законы распределения.
Понятие, аналогичное понятию условной вероятности для случайных событий 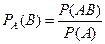 , можно ввести для характеристики зависимости между случайными величинами.
, можно ввести для характеристики зависимости между случайными величинами.
Рассмотрим отдельно случаи дискретной и непрерывной двумерной случайной величины.
а) Для дискретной двумерной сдучайной величины, заданной таблицей:

| 
| |||||
| 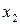
| 
| 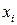
| 
| 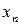
| |
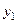
| 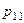 
| 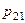
| 
| 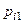
| 
| 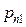
|

| 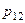
| 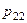
| 
| 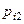
| 
| 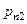
|

| 
| 
| 
| 
| 
| 
|
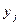
| 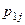
| 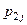
| 
| 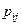
| 
| 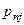
|

| 
| 
| 
| 
| 
| 
|
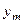
| 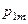
| 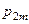
| 
| 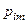
| 
| 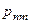
|
условные вероятности вычисляются по формулам:
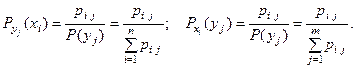
Замечание. Суммы соответствующих условных вероятностей равны единице, т.е.
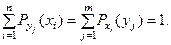
Пример 4. Пусть дискретная случайная величина задана таблицей:
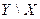
| |||
| -1 | 0,12 | 0,28 | 0,11 |
| 0,21 | 0,14 | 0,14 |
Найти условный закон распределения составляющей  при условии, что случайная величина
при условии, что случайная величина  приняла значение
приняла значение 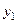 .
.
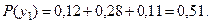
Тогда 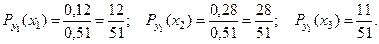
Очевидно, что сумма этих вероятностей равна единице.
б) Для Непрерывной двумерной случайной величины услов -ной плотностью распределения 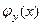 составляющей
составляющей  при данном значении
при данном значении 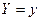 называют отношение
называют отношение
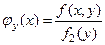 ,
,
аналогично, условной плотностью распределения 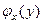 при данном значении
при данном значении 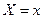 -
- 
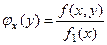 .
.
Пример 5. Пусть плотность совместного распределения не- прерывной двумерной случайной величины 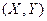 задана функцией:
задана функцией: 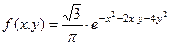 . Найти условные плотности распределения составляющих.
. Найти условные плотности распределения составляющих.
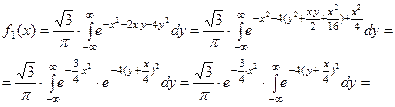
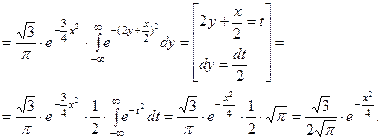
При вычислении использовали интеграл Пуассона
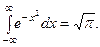
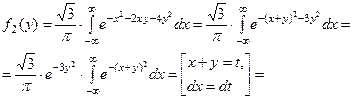
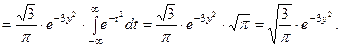
Тогда условные плотности распределения имеют вид:
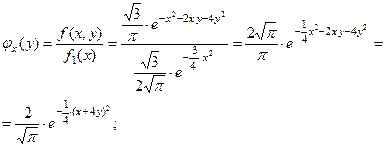
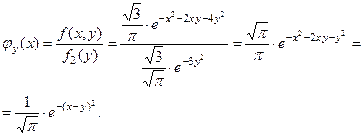
8.3 Условное математическое ожидание.
Определение. Условным математическим ожиданием диск- ретной случайной величины  при
при 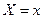 называется сумма произведений возможных значений
называется сумма произведений возможных значений  на их условные вероят -ности:
на их условные вероят -ности:
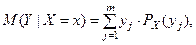
аналогично 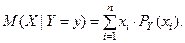
Пример 6. Пусть двумерная дискретная случайная величи -на задана таблицей:
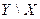
| |||
| -1 | 0,12 | 0,28 | 0,11 |
| 0,21 | 0,14 | 0,14 |
Найти условные математические ожидания:  при
при 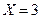 и
и  при
при 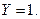
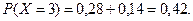
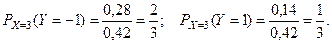
Тогда 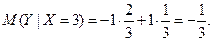
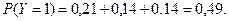
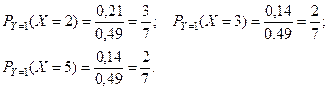
Тогда 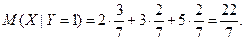
Для непрерывных величин:
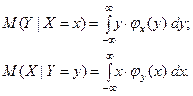
8.4 Зависимые и независимые случайные величины.
Определение. Две случайные величины называются незави- симыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая случайная величина. Из этого определения следует, что условные законы распределения независимых случайных величин равны их бе – зусловным законам распределения.
ТЕОРЕМА. Для того, чтобы случайные величины  и
и  были независимыми, необходимо и достаточно, чтобы выпол -нялось равенство:
были независимыми, необходимо и достаточно, чтобы выпол -нялось равенство: 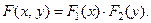
Доказывать теорему не будем, но как следствие, получаем:
Следствие. Для того, чтобы случайные величины  и
и  были независимыми, необходимо и достаточно, чтобы плот -ность совместного распределения системы
были независимыми, необходимо и достаточно, чтобы плот -ность совместного распределения системы 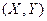 была рав -на произведению плотностей распределения составляющих, т.е.
была рав -на произведению плотностей распределения составляющих, т.е.

8.5 Числовые характеристики системы двух случайных
величин. Корреляционный момент. Коэффициент
корреляции.
Определение. Корреляционным моментом 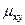 системы слу- чайных величин
системы слу- чайных величин  и
и  называют математическое ожидание произведения отклонений этих величин:
называют математическое ожидание произведения отклонений этих величин:
Дата публикования: 2014-11-04; Прочитано: 850 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
