Случайные величины 4 страница

Если мы рассматриваем дискретную случайную величину , принимающую значения ,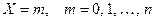

вероятности каждого из которых вычисляются по формуле Бернулли, т.е. имеющую биномиальное распределение, то 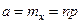, , 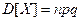и неравенство Чебышева приоб- ретает вид: 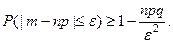(3)

Для частоты события в серии из 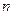независимых испы- таний, в каждом из которых оно может произойти с одной и той же вероятностью 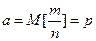, и имеющей дисперсию 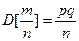, вероятность отклонения относительной частоты события от его вероятности оценивается с помощью формулы:

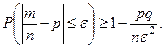
Пример. Вероятность появления события в каждом незави -симом испытании равна 0,4. Используя неравенство Чебышева,

Оценить вероятность того, что при 100 независимых испыта –ниях число появлений события заключено в промежутке от 30 до 50.

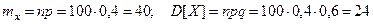. Требуемое число появлений события представляет собой про -межуток, симметричный относительно математического ожи –дания. Тогда 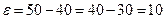. По формуле (3) получаем .

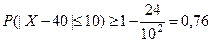5.3 Теорема Чебыщева.

ТЕОРЕМА. Если последовательность попарно независимых случайных величин имеет конечные мате- матические ожидания и дисперсии этих случайных величин равномерно ограничены (не превышают некоторого постоянного значения 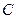), то среднее арифметическое этих случайных ве –личин сходится по вероятности к среднему арифметическому их математических ожиданий, т.е. для любого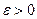

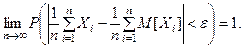(4)

В этой теореме предполагалось, Что сучайные величины имеют различные математические ожидания, но на практике чаще бывает, что в последовательности испытаний случайные величины имеют одно и тоже математическое ожидание и дис- персии их равномерно ограничены. В этом случае формула (4) приобретает вид:

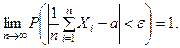(5)

Теорема Чебышева справедлива как для дискретных, так и для непрерывных случайных величин.

Сущность теоремы Чебышева состоит в том, что среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограни- чены) утрачивает характер случайной величины.

На теореме Чебышева основан широко применяемый в ста- тистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке элементов не -которой совокупности судят о поведении всей совокупности (генеральной совокупности). Например, при проверке качества каких – либо изделий проверяется некоторое количество слу - чайно взятых деталей.

Пример. Для проверки средней продолжительности службы электроламп в партии тз 400 одинаковых ящиков по выбору взяли по одной лампе из каждого ящика. Оценить вероятность того, что средняя продолжительность службы 400 электроламп отличается от средней продолжительности службы электро -ламп из всей партии не более чем на 5 ч. (по абсолютной ве- личине), если известно, что среднее квадратическое отклоне -ние продолжительности службы электроламп для каждого ящи- ка меньше чем 8 часов.

Пусть 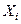- продолжительность службы электролампы, взя- той из 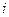- го ящика. По условию, 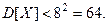Очевидно, что средняя продолжительность службы отобранных элек- троламп равна 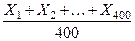, а средняя продолжи -тельность службы электроламп из всей партии равна

.

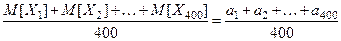Тогда вероятность искомого события

5.4 Теорема Бернулли.

ТЕОРЕМА. Пусть произведены 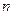независимых испытаний,

в каждом из которых постоянна вероятность появления собы -тия 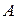: 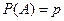. Тогда при неограниченном числе испыта- ний отклонение относительной частоты события от его веро –ятности имеет свойство:

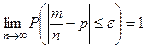
для любого .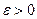

Другими словами, теорема Бернулли утверждает, что при 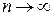относительная частота события стремится «по вероят- ности» к истинной вероятности этого события.

5.5 Центральная предельная теорема.

Закон больших чисел устанавливает факт приближения среднего значения большого числа случайных величин к оп -ределённым постоянным значениям. Более того, оказывается, что при некоторых условиях совокупное действие случайных величин приводит к определённому, а именно к нормальному закону распределения.

Центральная предельная теорема представляет собой группу теорем, посвящённых установлению условий, при ко –торых возникает нормальный закон распределения. Среди этих теорем важнейшее значение принадлежит теореме Ляпунова.

ТЕОРЕМА ЛЯПУНОВА. Если 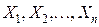- независи - мые случайные величины, для каждой из которых математи – ческое ожидание 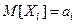, дисперсия 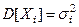, абсо- лютный центральный момент 3 – го порядка

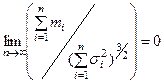и , (6)

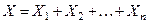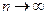то закон распределения суммы при неограниченно приближается к нормальному закону с матема -тическим ожиданием 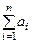и дисперсией 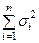. Условие (6) состоит в том, что в сумме не должно быть слагаемых, влияние которых на сумму было бы подав -ляюще высоко, по сравнению с остальными, т.е. «удельный вес» каждого слагаемого должен стремиться к нулю при увели- чении числа слагаемых.

Так например, потребление электроэнергии для бытовых нужд в каждой квартире многоквартирного дома можно пред- ставить в виде суммы 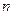различных случайных величин. Если потребление электроэнергии в каждой квартире не выделяется резко среди остальных, то, на основании теоремы Ляпунова,

можно считать, что потребление электроэнергии всего дома (т.е. суммарный закон распределения) будет иметь приближён- но нормальный закон распределения. Но если в некотором помещении этого дома расположена, к примеру мастерская по ремонту электрооборудования, работа которой связана с боль -шим расходом электроэнергии, то вывод о нормальном распре- делении электроэнергии в этом доме будет неверным, так как нарушено условие (6) теоремы Ляпунова.

§ 6. ФУНКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА ЕЁ

РАСПРЕДЕЛЕНИЕ И МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ

Если каждому значению случайной величины соответ- ствует одно из возможных значений случайной величины , то называют функцией случайного аргумента :

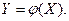
6.1. Пусть - дискретная случайная величина.

а) Если различным значениям случайной величины отве- чают различные значения случайной величины , то вероят -ности соответствующих значений и равны между собой.

Пример 1. Дискретная случайная величина задана рядом распределения:

	- 2	-1
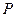
	0,2	0,1	0,1	0,3	0,3

Тогда закон распределения функции 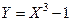задаётся рядом:

	- 9	-2	-1
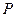
	0,2	0,1	0,1	0,3	0,3

б) Если различным значениям отвечают значения случай- ной величины , среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений .

Пример 2. Пусть случайная величина задана тем же рядом распределения:

	- 2	-1
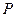
	0,2	0,1	0,1	0,3	0,3

Тогда ряд распределения случайной величины 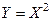имеет вид:

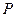
	0,1	0,4	0,5

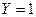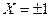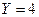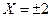( при , поэтому складываем соответствующие вероятности 0,1+0,3=0,4; при , поэтому скла- дываем вероятности 0,2+0,3=0,5).

6.2. Пусть теперь - непрерывная случайная величина,

заданная плотностью распределения 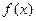. Пусть функция 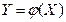- дифференцируемая и сторого монотонная, т.е. имеет дифференцируемую обратную функцию . Тог -да плотность распределения случайной величины 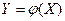гаходится с помощью равенства:

.

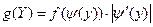Пример 3. Пусть случайная величина распределена по закону Коши

.

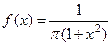Найти плотность распределения случайной величины .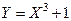

Обратная функция 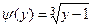. Эта функция строго монотонна и дифференцируема

.

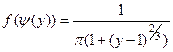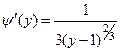. Тогда плотность распределения случай- ной величины 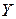имеет вид:

.

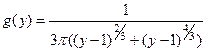Если функция 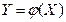в интервале возможных значений не монотонна, то стоит разбить этот интервал на интер- валы, в каждом из которых функция 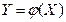является мо- нотонной, найти 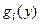для каждого из интервалов монотон –ности и затем представить 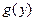в виде суммы:

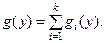
Пример 4. Задана плотность распределения нормально распределённой случайной величины :

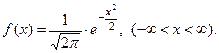
Найти плотность распределения 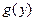случайной величины .

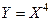Из уравнения 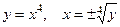. Так как на промежетке 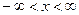функция 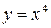не монотонна, то обратная функция состоит из двух частей. На промежутке ,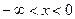

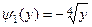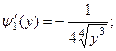
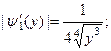
На промежутке

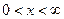
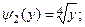
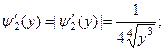
Тогда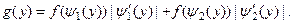

, .

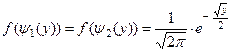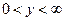Тогда

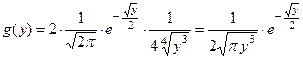
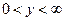и 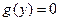вне этого интервала.

6.3. Пусть - дискретная случайная величина с возмож -

ными значениями 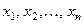, вероятности которых равны соответственно: 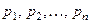. Функция 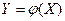также дискретная случайная величина, причём свои возможные зна- чения 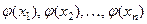она принимает с теми же ве- роятностями 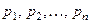. Тогда её математическое ожи- дание вычисляется по формуле:

.

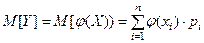Пример 5 Пусть дискретная случайная величина задана рядом распределения:

	- 2	-1
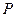
	0,2	0,1	0,1	0,3	0,3

Найти математическое ожидание случайной величины

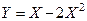. Это также дискретная случайная величина с рядом распределения:

	- 10	- 3		-1	- 6
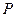
	0,2	0,1	0,1	0,3	0,3

Тогда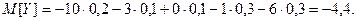

6.4. Пусть теперь - непрерывная случайная величина с плотностью распределения 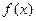. Чтобы найти математичес -кое ожидание функции 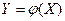, можно воспользоваться двумя способами:

а) сначала найти плотность распределения 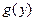данной функции и непосредственно применить формулу для вычисле -ния математического ожидания

;

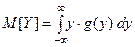б) если отыскание плотности 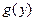вызывает затруднение, то математическое ожидание можно найти по формуле

.

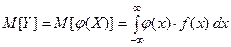Пример 6. Пусть задана плотность распределения случайной величины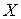

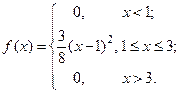
Найти математическое ожидание функции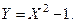

В этом примере математическое ожидание проще найти ис- пользуя способ б). Так как 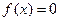вне промежутка 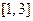, то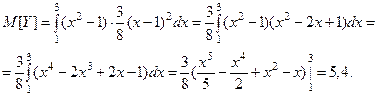

§ 7. ФУНКЦИЯ ДВУХ СЛУЧАЙНЫХ АРГУМЕНТОВ.

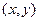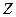Если каждой паре случайных величин и соответствует одно из возможных значений случайной величи- ны , то 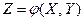называют функцией двух случайных агументов и . На практике наиболее часто встре- чается задача - найти закон распределения функции 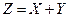по известным распределениям слагаемых. Напри- мер, если - погрешность показаний некоторого измеритель- ного прибора (распределена, обычно, нормально), а - погрешность округления показаний этого прибора (распределе- на равномерно), то возникает задача - найти закон распреде -ления суммы погрешностей .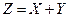

7.1. Пусть и - дискретные случайные величины,

которые заданы своими законами распределения. Тогда воз- можные значения случайной величины 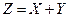- это все возможные значения сумм значений и , а вероятности соответствующих значений 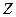находятся, как произведения со- ответствующих вероятностей значений и , входящих в

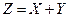и как суммы этих произведений, в случае, если одному значению суммы отвечают различные комбинации значений и .

Пример 1. Пусть даны ряды распределения дискретных случайных величин и .

	-1
	0,2	0,5	0,3

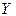
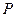
	0,1	0,4	0,5

Тогда функция 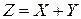принимает значения: 1, 3, 4, 6, 7, 8, 9. Вероятности этих значений находим, используя теоре -мы умножения и сложения вероятностей следующим образом:

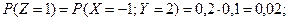
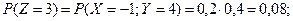
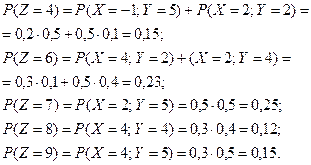
Получаем ряд распределения случайной величины :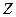

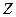
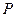
	0,02	0,08	0,15	0,23	0,25	0,12	0,15

Сумма вероятностей, стоящих в нижней строке, равна 1, поэтому эта таблица в самом деле задаёт ряд распределения случайной величины .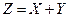

7.2. Пусть теперь и - непрерывные случайные величины. Если и - независимы, то зная плотности таспределения случайных величин и - 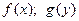, соответственно, плотность распределения случайной величины

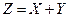можно найти по одной из следующих формул:

;

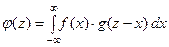или