Теорема Остроградского - Гаусса

Если в некоторой области G трёхмерного пространства, ограниченной замкнутой кусочно-гладкой поверхностью , задано непрерывно дифференцируемое векторное поле 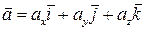, то поток векторного поля 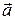через внешнюю сторону замкнутой поверхности равен тройному интегралу от функции 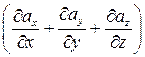по области G, ограниченной поверхностью :

,

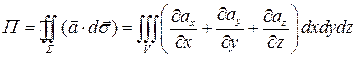где символ обозначает интеграл по замкнутой поверхности.

Доказательство:

а) Рассмотрим область G, правильную в направлении оси Oz, которую будем называть элементарной H_z областью. Это означает, что снизу и сверху она ограничена поверхностями: : и : 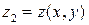соответственно, а сбоку цилиндрической поверхностью 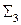с образующими, параллельными оси Oz и направляющей Г.

Рассмотрим одно слагаемое:

= =

= =…

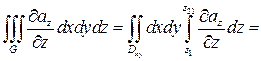
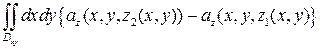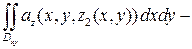
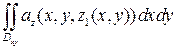{на 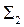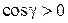, а на .

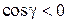Учитывая, что 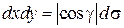, получаем:

на : ,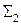

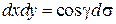на : } …= + =…

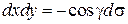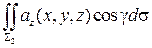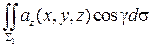Добавим интеграл по 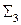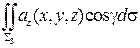в полученную сумму, так как на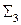 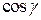всюду равен нулю, а следовательно, и .

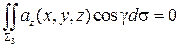Тогда

…= + + =

= .

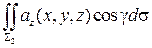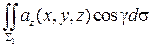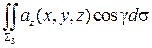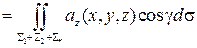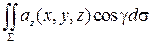б) Рассмотрим пространственную область G, которую можно разбить на n элементарных областей H_z типа, т.е. 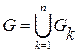. Докажем, что и в этом случае справедлива теорема Остроградского-Гаусса.

Пусть , , 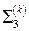- нижняя, верхняя и боковая части поверхности , ограничивающей область ,

тогда

+ + = ,

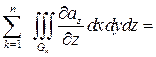
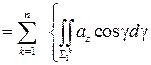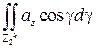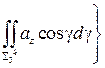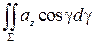так как интегралы по 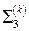равны нулю, а по поверхност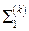и и 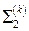составляют в сумме интеграл по поверхности .

в) Аналогично для H_x и H_y областей справедливо:

; .

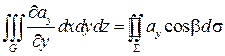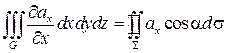Складывая почленно, получаем утверждение теоремы.

1). Векторная форма записи теоремы Остроградского-Гаусса имеет вид:

,

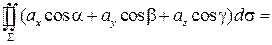
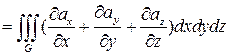где 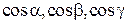- координаты единичного вектора внешней нормали.

2). Используя обозначение дивергенции, формулу Остроградского-Гаусса можно записать в виде

.

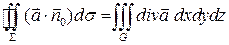Поток векторного поля (вектора) через внешнюю сторону замкнутой поверхности равен тройному интегралу от 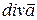по области G, ограниченной .

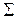Применение теоремы Остроградского – Гаусса

Вычисление объемов.

ПРИМЕР. Пусть ; ; . , .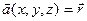

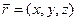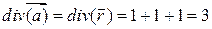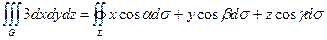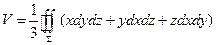Вычисление потоков.

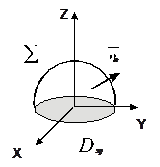
ПРИМЕР. Вычислите поток поля 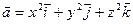через замкнутую поверхность .

Решение:

= = =…

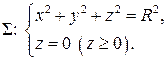
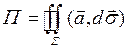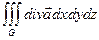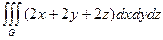{перейдём в сферическую систему координат} …= = .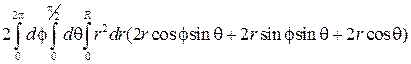

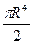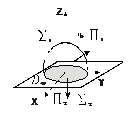
ПРИМЕР. Найдите поток поля 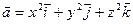через внешнюю сторону полусферы:

Решение:

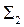Воспользуемся результатами предыдущей задачи. Замкнем поверхность поверхностью , которая представляет собой часть плоскости XOY.

, , = =…{ }… = ,

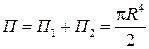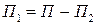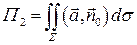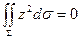т.к. на 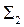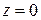и = .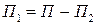

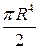Инвариантное определение дивергенции

Пусть 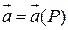- векторное поле, удовлетворяющее условию теоремы Остроградского – Гаусса. Пусть точка M - произвольная точка области G. Выберем поверхность , охватывающую область G. Из теоремы Остроградского – Гаусса следует, что .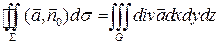

Воспользуемся теоремой о среднем, согласно которой существует такая точка М ₁, принадлежащая G, что 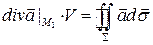; 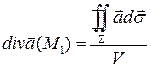, где V –объем G. Пусть стягивается в точку М, тогда М ₁→ М, а → , .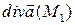

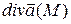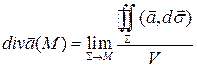Поскольку правая часть выражения не зависит от системы координат (инвариантна), то инвариантно и данное ОПРЕДЕЛЕНИЕ дивергенции.