Производная по направлению

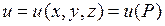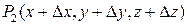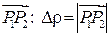Пусть в пространственной области G задано скалярное поле: . Рассмотрим точку и исходящий из нее вектор . Найдем, как изменяется поле в направлении вектора . Сместимся из точки в направлении вектора в точку . Обозначим за длину вектора , тогда 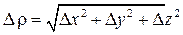. При этом функция поля получит приращение

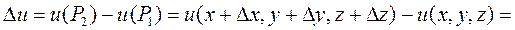
где - бесконечно малая более высокого порядка по 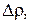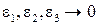при , а величина 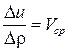- средняя скорость изменения скалярной функции в направлении вектора .

.

Перейдем к пределу при 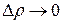,что соответствует стремлению :

,

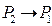где 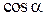, , 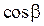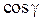- направляющие косинусы вектора 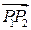. Поскольку 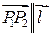, то их направляющие косинусы равны. Так как 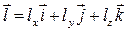, то , , .

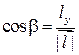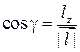ОПРЕДЕЛЕНИЕ. Производной функции u в точке 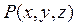(обозначение ) по направлению вектора 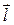называется предел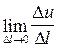 (если он существует), равный .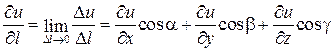

Производная по направлению 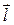: - определяет скорость изменения скалярного поля в направлении вектора 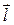, в частности, если >0, поле возрастает, если <0, поле убывает.

ПРИМЕР. Найдите производную в точке Р (1,1,1) в направлении вектора , если .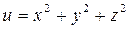

Решение:

; ,

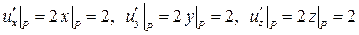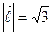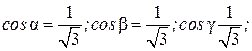
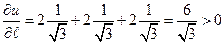, следовательно, скалярное поле возрастает.