 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод введения топологии с помощью базы
|
|
Если 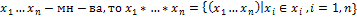
Утв.1 Пусть x – непустое мн-во β -семейств.
Подмн-во мн-ва x, удовл. усл.
В1) Uβ=xu
В2)  V1, V2
V1, V2 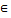 β и
β и  x
x  V1 ∩ V2 ∃ U
V1 ∩ V2 ∃ U  β | x
β | x  V ⊆ V1 ∩ V2
V ⊆ V1 ∩ V2
тогда ∃ единственная топология  на мн-ве X, такая что β является базой пр-ва (x,
на мн-ве X, такая что β является базой пр-ва (x,  )
)
□ Рассм. семейство  опр. по правилу:
опр. по правилу:
∅ 
 , U
, U 
 ó
ó  x
x  U ∃ U
U ∃ U  β | x
β | x  V ⊆ U
V ⊆ U
Покажем, что  - топология на X.
- топология на X.
□ 01) ∅ 
 , x
, x 
 (Из В1)
(Из В1)
02) Покажем, что пересечение  конечн. совокуп. мн-в из
конечн. совокуп. мн-в из  принадл.
принадл. 
(□ индук. по числу n мн-в пересек. совокупн.)
n=1 – выполн.
Пусть утв. верно для сов-тей с числом мн-в n=2. Покажем, что оно верно для совокуп. с числ. n=k+1
Пусть U=U1∩…∩Uk+1, где Ui 
 , i=1,k+1
, i=1,k+1
Обозн. U*= U1∩…∩Uk, U* 

U= U* ∩ Uk+1 , пусть x  U ∃ V1
U ∃ V1  β | λ
β | λ  U1 ⊆ U*
U1 ⊆ U*
∃ V2  β| x
β| x  U2 ⊆ Uk+1
U2 ⊆ Uk+1
∃ U  β| x
β| x  U ⊆ V1∩ V2, V ⊆ U => U
U ⊆ V1∩ V2, V ⊆ U => U 

03)Пусть U=VUt, где где  t
t 
 Ut
Ut 

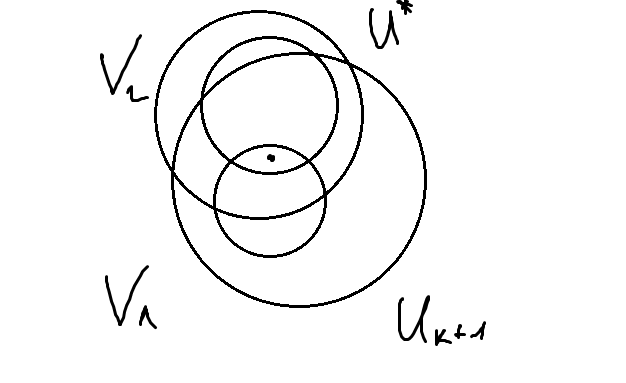
Покажем, что U 
 , рассмотрим
, рассмотрим  т.к.
т.к. 
 ∃ t0
∃ t0 
 | x
| x  U0
U0
∃V  β|| x
β|| x  V ⊆ U0 V ⊆ U ▪
V ⊆ U0 V ⊆ U ▪
β – база пр-ва (x,  )
)
Лемма: Пусть даны т.п. 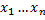 , x=
, x= 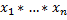
Семейство βn подмн-в мн-ва x, сост. Из всех мн-в вида 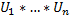 , где
, где  i=1,n Ui⊆xi
i=1,n Ui⊆xi
удл. Условиям B1, B2.
□B1: 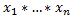
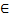 βn
βn
B2: 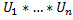
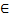 βn
βn 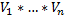
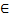 βn
βn
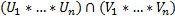 =
= 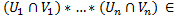 βn ▪
βn ▪
23 Определение топологии произведения топологических пространств. Теорема о метричности этой топологии. Примеры.
Опр.
Пусть даны т.п. 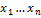 , x=
, x= 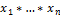 Топологией произведения на Х наз. топология
Топологией произведения на Х наз. топология  r базу которой образует сем-во βn
r базу которой образует сем-во βn
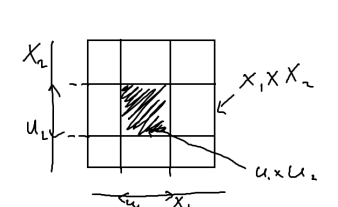
Утв.
Пусть  – т.п. x=
– т.п. x=  Если каждое из пр-в x: метризуемо метрикой p, то х метриз. метрикой p(x,y)=max pi(xi,yi)
Если каждое из пр-в x: метризуемо метрикой p, то х метриз. метрикой p(x,y)=max pi(xi,yi)
x= 
y= 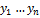
□ 1)покажем, что p-метрика
М1), М2) очевидно
М3) p(x,y) ≤p(x,z)+p(z,y)
 i=1,n pi(xi,yi) ≤pi(xi,ei)+pi(zi,yi) ≤p(x,z)+p(z,y)
i=1,n pi(xi,yi) ≤pi(xi,ei)+pi(zi,yi) ≤p(x,z)+p(z,y)
p(x,y) ≤p(x,z)+p(z,y)
2)Вид шара, пусть a=(ai…ak)  X, ε>0
X, ε>0
x=(x1…xn)  βp(a, ε) ó p(a,x)< ε ó
βp(a, ε) ó p(a,x)< ε ó
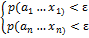 ó
ó 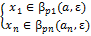
β(a, ε)= βp1(a1, ε)*… βpn(an, ε)
Вывод:  a
a  X,
X,  ε>0 βp(a, ε)
ε>0 βp(a, ε) 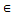 βn
βn
3)Покажем, что  P=
P=  n пок.
n пок.  p
p
пусть G 
 P, когда
P, когда  a
a 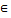 G ∃ εa>0 | βp (a, εa)
G ∃ εa>0 | βp (a, εa)  G,
G,
Т.к. все βp (a, εa) 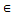 βn и G= ∪ βp(a, ε0) G
βn и G= ∪ βp(a, ε0) G 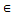
 n
n
Покажем  n ⊆
n ⊆  P, пусть G
P, пусть G 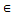
 p, рассм.
p, рассм.  a=(a1…an)
a=(a1…an)  G ∃
G ∃ 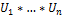 |
|  a
a  ⊆ G
⊆ G
Ui⊆xi i=1,n  i=1,n ∃ εi>0| βp(ai, εi) ⊆ Ui
i=1,n ∃ εi>0| βp(ai, εi) ⊆ Ui
ε=min{ε1…εn}, тогда βp(a, ε)= 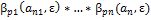 ⊆
⊆ 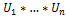 ⊆G▪
⊆G▪
Примеры:
1)На ℝn= 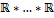
 n=
n=  n μ(x,y)=max|xi-yi|
n μ(x,y)=max|xi-yi|
 n(из утв.2) μ~d=>
n(из утв.2) μ~d=>  n=
n=  n
n
2)В ℝn рассм. фигуры
П: 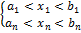
Где ai<bi i=1,n
П=  Топология произведения на П сов. с топ., из ℝn
Топология произведения на П сов. с топ., из ℝn
24 Сходимость последовательностей в произведении топологических пространств.
Утв. Пусть x= 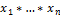 , где
, где 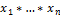 -т.п. λ=(x1…xn)
-т.п. λ=(x1…xn) 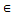 X (X(k))k=1 послед. в х-точек, х(к)=(х1(к) … хn(k))
X (X(k))k=1 послед. в х-точек, х(к)=(х1(к) … хn(k))
x(k)a-> x в x ó  i=1,n xi(k)->xi в xi
i=1,n xi(k)->xi в xi
□=>)fix  i ≤ n Рассм.
i ≤ n Рассм.  окр. U топ. xi в Xi
окр. U топ. xi в Xi
Рассм. G= 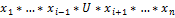 - опр. точки х в Х
- опр. точки х в Х
∃ p  ℕ |
ℕ |  k ≥ p x(k)
k ≥ p x(k)  G Тогда
G Тогда  k≥p x1(k)
k≥p x1(k) 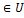
<=)Рассмотрим  окр. G=
окр. G= 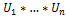 точки х в Х
точки х в Х
 i=1,n ∃ pi
i=1,n ∃ pi  ℕ |
ℕ |  k≥pi xi(k)
k≥pi xi(k)  Ui
Ui
Пусть p=max {p1…pn};  k≥p x(k)
k≥p x(k)  G ▪
G ▪
Дата публикования: 2015-11-01; Прочитано: 230 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
