 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Сравнения первой степени. Линейные диофантовы
|
|
Уравнения.
Пусть а, b – целые числа, m – натуральное число. Говорят, что а сравнимо с b по модулю m, если 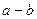 делится на m. В этом случае будем писать
делится на m. В этом случае будем писать 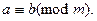
Приведем основные свойства сравнений:
1)  ;
;
2) если 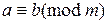 , то
, то 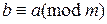 ;
;
3) если 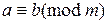 ,
, 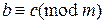 , то
, то 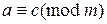 ;
;
4) если 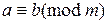 , то
, то 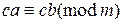 ;
;
5) если 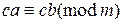 ,
, 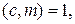 то
то 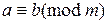 ;
;
6) если 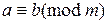 , то
, то 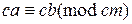 ;
;
7) если 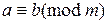 ,
, 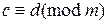 , то
, то 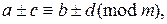
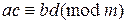 ;
;
8) если 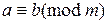 , то
, то 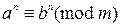 для любого натурального n;
для любого натурального n;
9) если 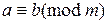 ,
, 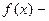 многочлен с целыми коэффициентами, то
многочлен с целыми коэффициентами, то 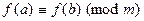 ;
;
10) 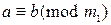 ,…,
,…, 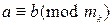 тогда и только тогда, когда
тогда и только тогда, когда 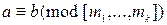 ;
;
11) если 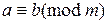 и m делится на d, то
и m делится на d, то 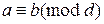 ;
;
12) если 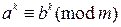 и n делится на k, то
и n делится на k, то 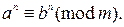
Пусть а, b – целые числа, 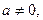 m – натуральное число. Сравнение
m – натуральное число. Сравнение 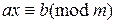 называется разрешимым, если существует целое число
называется разрешимым, если существует целое число 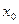 такое, что
такое, что 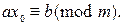 В этом случае число
В этом случае число 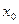 называется решением сравнения
называется решением сравнения 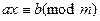 .
.
Сравнение 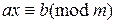 разрешимо тогда и только тогда, когда b делится на (a, m). Причем, если
разрешимо тогда и только тогда, когда b делится на (a, m). Причем, если 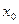 - это одно из решений сравнения
- это одно из решений сравнения 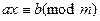 , то множество всех решений этого сравнения имеет вид
, то множество всех решений этого сравнения имеет вид  , т.е.
, т.е. 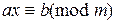
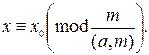
Вышеуказанное решение линейного сравнения 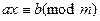 позволяет найти все решения линейного диофантова уравнения
позволяет найти все решения линейного диофантова уравнения 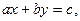 где
где 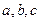 – целые числа,
– целые числа, 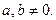 Диофантово уравнение
Диофантово уравнение 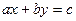 имеет решение в целых числах x, y тогда и только тогда, когда с делится на (a,b). Причем, если
имеет решение в целых числах x, y тогда и только тогда, когда с делится на (a,b). Причем, если 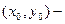 это одно из решений этого уравнения, то множество всех решений задается в виде
это одно из решений этого уравнения, то множество всех решений задается в виде 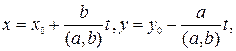 где t пробегает множество всех целых чисел. Частное решение
где t пробегает множество всех целых чисел. Частное решение 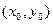 можно найти с помощью алгоритма Евклида. Индукцией по числу переменных аналогичным образом можно решить линейное диофантово уравнение от n переменных
можно найти с помощью алгоритма Евклида. Индукцией по числу переменных аналогичным образом можно решить линейное диофантово уравнение от n переменных 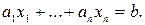
Пусть  попарно взаимно простые натуральные числа и
попарно взаимно простые натуральные числа и 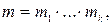 а
а 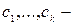 целые числа, тогда множество решений системы сравнений
целые числа, тогда множество решений системы сравнений 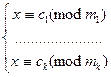 имеет вид
имеет вид 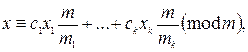 где
где 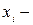 произвольное целое число, удовлетворяющее сравнению
произвольное целое число, удовлетворяющее сравнению 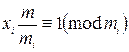 (китайская теорема об остатках).
(китайская теорема об остатках).
Пример 1. Решите сравнение 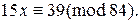
Решение. С помощью алгоритма Евклида найдем частное решение 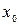 исходного сравнения. Имеем 84=15·5+9,15=9·1+6,9=6·1+3,6=3·2+0. Поэтому 3=9–6·1=9–(15–9·1)·1=9·2–15·1=(84–15·5)·2–15·1=84·2+15·(–11), следовательно, 39=3·13=84·26+15·(–143), т.е. 15·(–143)≡39(mod 84), значит,
исходного сравнения. Имеем 84=15·5+9,15=9·1+6,9=6·1+3,6=3·2+0. Поэтому 3=9–6·1=9–(15–9·1)·1=9·2–15·1=(84–15·5)·2–15·1=84·2+15·(–11), следовательно, 39=3·13=84·26+15·(–143), т.е. 15·(–143)≡39(mod 84), значит, 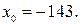 Поэтому множество всех решений исходного сравнения имеет вид
Поэтому множество всех решений исходного сравнения имеет вид 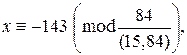 т.е.
т.е. 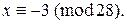
Пример 2. Решите уравнение 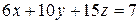 в целых числах.
в целых числах.
Решение. Зафиксируем переменную 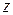 и рассмотрим исходное уравнение как диофантово уравнение относительно переменных
и рассмотрим исходное уравнение как диофантово уравнение относительно переменных 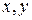 . Уравнение
. Уравнение 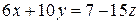 разрешимо тогда и только тогда, когда
разрешимо тогда и только тогда, когда 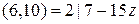 , то есть при
, то есть при 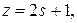
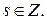 Поэтому
Поэтому 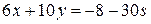 . Найдем частное решение
. Найдем частное решение 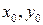 . Используя алгоритм Евклида, находим линейное разложение наибольшего общего делителя чисел 6 и 10:
. Используя алгоритм Евклида, находим линейное разложение наибольшего общего делителя чисел 6 и 10:
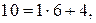
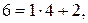
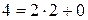
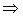
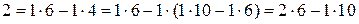 . Поэтому
. Поэтому 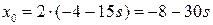 ,
, 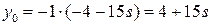 . Общее решение исходного уравнения:
. Общее решение исходного уравнения: 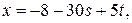
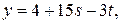
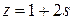 , где
, где 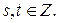
Ответ: 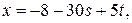
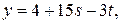
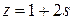 , где
, где 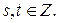
Пример 3. Решите систему сравнений 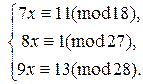
Решение. Преобразуем исходную систему:
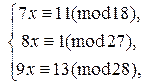
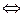
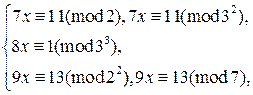

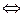
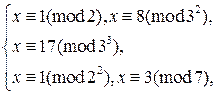
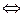
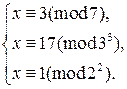
К последней системе применим китайскую теорему об остатках. Найдем частные решения сравнений 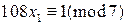 ,
, 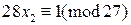 ,
, 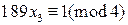 . Имеем
. Имеем 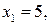
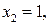
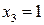 . Поэтому решение исходной системы имеет вид:
. Поэтому решение исходной системы имеет вид: 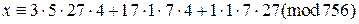 , то есть
, то есть 
Пример 4. Решите систему уравнений 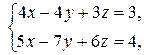 в целых числах.
в целых числах.
Решение. Решаем систему методом Гаусса:
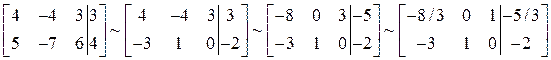 .
.
Откуда следует, что 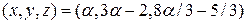 ,
, 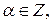
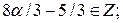 . Следовательно,
. Следовательно, 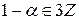 , т.е.
, т.е. 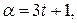
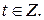 Окончательно получаем
Окончательно получаем 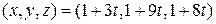 ,
, 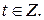
2.1. Решите следующие сравнения:
1) 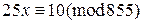 , 2)
, 2) 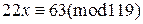 , 3)
, 3) 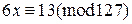 ,
,
4) 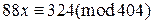 .
.
2.2. Решите следующие уравнения в целых числах:
1)  2)
2) 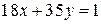 , 3)
, 3)  ,
,
4) 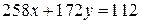 , 5)
, 5)  .
.
2.3. Решите следующие уравнения в целых числах:
1) 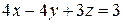 , 2)
, 2) 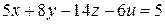 ,
,
3) 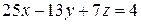 ,4)
,4) 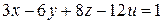 .
.
2.4. Пусть 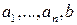 - целые числа, не все из которых равны 0.
- целые числа, не все из которых равны 0.
1) Докажите, что уравнение 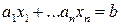 разрешимо в целых числах тогда и только тогда, когда
разрешимо в целых числах тогда и только тогда, когда 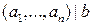 .
.
2) Пусть 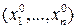 - частное решение неоднородного уравнения
- частное решение неоднородного уравнения 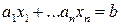 ,
, 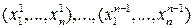 - линейно независимые решения однородного уравнения
- линейно независимые решения однородного уравнения 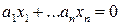 . Докажите, что общее решение неоднородного уравнения
. Докажите, что общее решение неоднородного уравнения 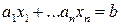 задается формулой
задается формулой 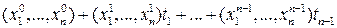 , где
, где 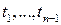 - произвольные целые числа.
- произвольные целые числа.
2.5. Используя китайскую теорему об остатках, решите следующие
системы сравнений:
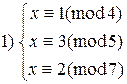 2)
2)  3)
3) 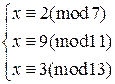
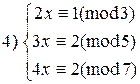 5)
5) 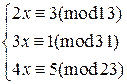 6)
6) 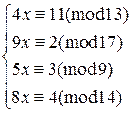
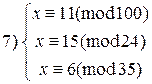 8)
8) 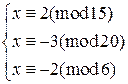 9)
9) 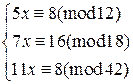 .
.
2.6. Решите следующие системы уравнений в целых числах:
1) 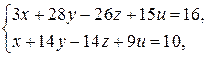 2)
2) 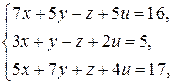
3) 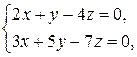 4)
4) 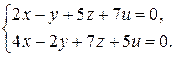
2.7. Найдите все натуральные решения уравнения 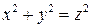 .
.
2.8. Докажите, что уравнение 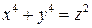 не имеет решений в натуральных числах.
не имеет решений в натуральных числах.
2.9. Пусть 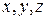 - целые числа, удовлетворяющие равенству
- целые числа, удовлетворяющие равенству
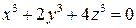 . Докажите, что
. Докажите, что 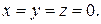
2.10. Докажите, что уравнение 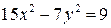 не имеет решений в целых числах.
не имеет решений в целых числах.
2.11. Докажите, что для любого натурального 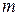 найдутся целые числа
найдутся целые числа 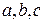 , такие, что уравнение
, такие, что уравнение 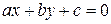 имеет ровно
имеет ровно 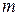 решений в натуральных числах
решений в натуральных числах 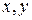 .
.
2.12. Докажите, что для любых натуральных 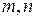 найдутся целые числа
найдутся целые числа 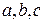 , такие, что уравнение
, такие, что уравнение 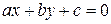 имеет единственное решение
имеет единственное решение 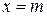 ,
, 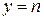 в натуральных числах.
в натуральных числах.
2.13. Найдите все простые числа 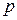 и натуральные числа
и натуральные числа 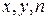 , удовлетворяющие уравнению
, удовлетворяющие уравнению 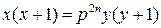 .
.
Функция Эйлера.
Пусть m – натуральное число, большее единицы. Количество натуральных чисел, меньших m, которые взаимно просты с m, обозначается 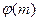 и функция
и функция 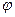 называется функцией Эйлера.
называется функцией Эйлера.
По определению полагается 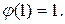
Отметим, что функция Эйлера мультипликативна, т.е. для любых взаимно простых натуральных чисел m, n выполняется равенство 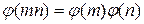 и если
и если 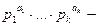 каноническое разложение числа m, то
каноническое разложение числа m, то
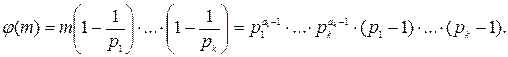
Пусть m – натуральное, а а – целые числа и 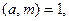 то
то 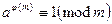 (теорема Эйлера).
(теорема Эйлера).
Следствием теоремы Эйлера является теорема Ферма: если p – простое, а а – целые числа, причем 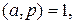 то
то 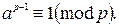 Теорему Ферма можно сформулировать иначе: пусть p – простое число, а – целое число, тогда
Теорему Ферма можно сформулировать иначе: пусть p – простое число, а – целое число, тогда 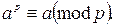
Говорят, что целые числа 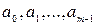 образуют полную систему вычетов по модулю m, если они попарно не сравнимы по модулю m. Целые числа
образуют полную систему вычетов по модулю m, если они попарно не сравнимы по модулю m. Целые числа 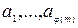 образуют приведенную систему вычетов по модулю m, если они взаимно просты с числом m и попарно не сравнимы между собой по модулю m. Легко проверить, что числа
образуют приведенную систему вычетов по модулю m, если они взаимно просты с числом m и попарно не сравнимы между собой по модулю m. Легко проверить, что числа 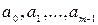 образуют полную систему вычетов по модулю m тогда и только тогда, когда эти числа дают различные остатки при делении на m.
образуют полную систему вычетов по модулю m тогда и только тогда, когда эти числа дают различные остатки при делении на m.
Пример 1. Используя теорему Ферма, вычислите остаток при делении 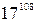 на 29.
на 29.
Решение. Имеем 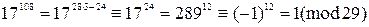 .
.
Пример 2. Используя теорему Эйлера и китайскую теорему об остатках, найдите остаток при делении 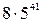 на 96.
на 96.
Решение. Пусть 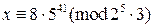 , тогда
, тогда 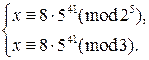
Используя теорему Эйлера, находим, что 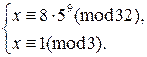
Далее 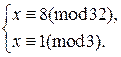
Используя китайскую теорему об остатках, находим 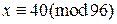 .
.
3.1. Вычислите: 1) 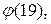 2)
2) 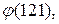 3)
3) 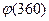 , 4)
, 4) 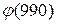 , 5)
, 5) 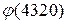 .
.
3.2. Сколько чисел от 1 до 120 не взаимно просты с числом 30?
3.3. Пусть p, q – простые числа, 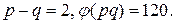 Найдите p, q.
Найдите p, q.
3.4. Пусть а, b – взаимно простые натуральные числа, р – простое число, 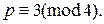 Докажите, что
Докажите, что 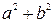 не делится на р.
не делится на р.
3.5. Найдите все простые числа р такие, что
1) числа 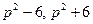 также являются простыми;
также являются простыми;
2) числа 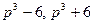 также являются простыми.
также являются простыми.
3.6. Пусть n – нечетное натуральное число. Докажите, что 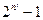 делится на n.
делится на n.
3.7. Используя теорему Ферма, вычислите следующие остатки:
1) 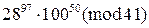 , 2)
, 2) 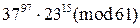 , 3)
, 3) 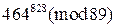 ,
,
4) 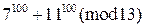 .
.
3.8. Используя теорему Ферма и китайскую теорему об остатках, вычслите следующие остатки:
1) 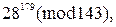 2)
2) 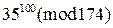 , 3)
, 3) 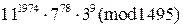 ,
,
4) 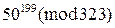 , 5)
, 5) 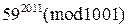 .
.
3.9. Используя теорему Эйлера, вычислите следующие остатки:
1) 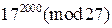 , 2)
, 2) 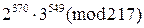 , 3)
, 3) 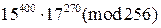 ,
,
4) 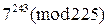 , 5)
, 5) 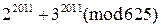 .
.
3.10. Используя теорему Эйлера и китайскую теорему об остатках, вычислите следующие остатки:
1) 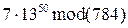 , 2)
, 2) 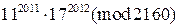 , 3)
, 3) 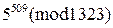 ,
,
4) 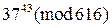 .
.
3.11. Докажите, что для любого простого числа 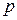 и любого целого числа
и любого целого числа 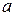 сравнение
сравнение 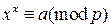 разрешимо.
разрешимо.
3.12. Найдите все натуральные числа 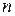 , для которых
, для которых 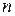 делится на
делится на 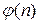 .
.
3.13. Докажите, что для простых 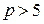 и натуральных
и натуральных 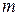 равенство
равенство
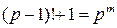 невозможно.
невозможно.
3.14. Пусть натуральные числа 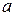 и
и 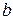 таковы, что
таковы, что 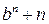 делится на
делится на 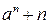 для любого натурального
для любого натурального 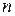 . Докажите, что
. Докажите, что 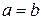 .
.
3.15. Найдите все простые числа 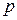 , такие, что
, такие, что 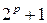 делится на
делится на 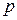 .
.
3.16. Найдите все натуральные 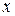 , удовлетворяющие равенству
, удовлетворяющие равенству
1) 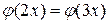 , 2)
, 2) 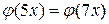 .
.
3.17. Докажите, что существует бесконечно много простых чисел вида
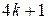
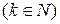 .
.
Дата публикования: 2015-11-01; Прочитано: 1779 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
