 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Показательные и полиномиальные сравнения. 5 страница
|
|
Пример 2. Найдите поле разложения 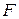 многочлена
многочлена 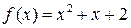 над полем
над полем 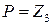 и укажите степень расширения
и укажите степень расширения 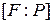 .
.
Решение. Многочлен 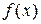 неприводим над
неприводим над 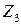 . Докажем, что
. Докажем, что 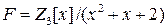 . Найдём решения уравнения
. Найдём решения уравнения 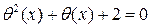 в факторкольце
в факторкольце 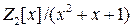 . Корнями уравнения являются элементы:
. Корнями уравнения являются элементы: 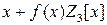 и
и 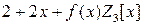 . Присоединяя корни, находим, что
. Присоединяя корни, находим, что 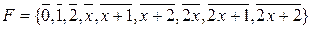 . То есть
. То есть 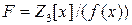 и
и 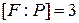 .
.
Пример 3. Докажите, что число 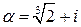 является алгебраическим.
является алгебраическим.
Решение. Имеем: 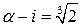 , a 3–3 a 2 i –3 a + i =2, a 3–3 a –2=(3 a 2–1) i, a 6+9 a 2+4–6 a 4–4 a 3+12 a =–9 a 4+6 a 2–1, a 6+3 a 4–4 a 3+3 a 2+12 a +5=0. Следовательно, число
, a 3–3 a 2 i –3 a + i =2, a 3–3 a –2=(3 a 2–1) i, a 6+9 a 2+4–6 a 4–4 a 3+12 a =–9 a 4+6 a 2–1, a 6+3 a 4–4 a 3+3 a 2+12 a +5=0. Следовательно, число 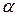 алгебраическое.
алгебраическое.
8.1. Какие из числовых множеств 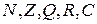 образуют поле относительно операций сложения и умножения?
образуют поле относительно операций сложения и умножения?
8.2. Докажите, что конечная область целостности является полем.
8.3. Докажите, что любое конечное поле имеет положительную характеристику.
8.4. Существует ли бесконечное поле положительной характеристики?
8.5. Докажите, что в поле 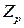 выполняются равенства:
выполняются равенства:
1) 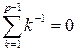 (
(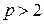 );
);
2) 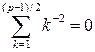 (
(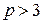 ).
).
8.6. Найдите минимальный многочлен для элемента 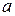 над полем
над полем 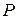 , если:
, если:
1) 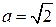 ,
, 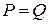 ;
;
2) 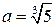 ,
, 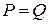 ;
;
3) 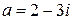 ,
, 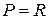 ;
;
4) 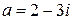 ,
, 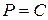 ;
;
5) 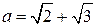 ,
, 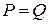 .
.
8.7. Докажите, что элемент 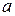 является алгебраическим над полем
является алгебраическим над полем 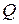 , если:
, если:
1) 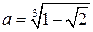 ;
;
2) 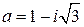 ;
;
3) 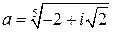 .
.
8.8. Найдите степень элемента 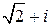 над полем
над полем 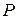 , если:
, если:
1) 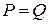 ;
;
2) 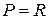 ;
;
3) 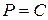 .
.
8.9. Докажите, что если многочлен 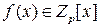 неприводим над полем
неприводим над полем 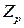 , то для любых
, то для любых 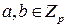 ,
, 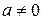 , многочлен
, многочлен 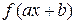 неприводим над полем
неприводим над полем 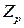 .
.
8.10. Пусть 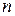 - натуральное число,
- натуральное число, 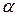 - действительное положительное число. Докажите, что если числа
- действительное положительное число. Докажите, что если числа 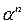 и
и 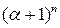 рациональные, то число
рациональные, то число 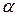 также рациональное.
также рациональное.
8.11. Пусть 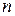 - натуральное число,
- натуральное число, 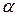 - комплексное число, такие, что числа
- комплексное число, такие, что числа 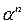 и
и 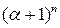 рациональные. Можно ли утверждать, что число
рациональные. Можно ли утверждать, что число 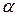 также рациональное?
также рациональное?
8.12. Найдите все неприводимые над полем 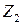 многочлены второй степени из
многочлены второй степени из 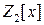 .
.
8.13. При каких значениях 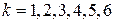 факторкольцо
факторкольцо 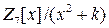 является полем?
является полем?
8.14. Применяя алгоритм Евклида, найти наибольший общий делитель многочленов 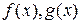 с коэффициентами из поля
с коэффициентами из поля 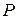 , если:
, если:
1) 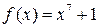 ,
, 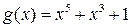 ,
, 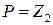 ;
;
2) 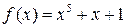 ,
, 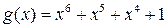 ,
, 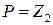 ;
;
3) 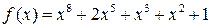 ,
, 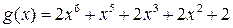 ,
, 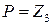 .
.
8.15. Докажите неприводимость многочленов 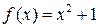 ,
, 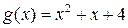 над полем
над полем 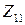 и построить изоморфизм факторколец
и построить изоморфизм факторколец 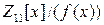 и
и 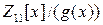 .
.
8.16. Вычислите образ 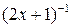 в факторкольце
в факторкольце 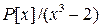 , если:
, если:
1) 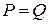 ;
;
2) 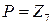 .
.
8.17. Решите сравнения:
1) 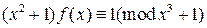 в
в 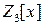 ;
;
2) 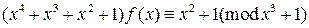 в
в 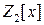 .
.
8.18. Найдите поле разложения 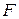 многочлена
многочлена 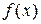 над полем
над полем 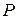 и укажите степень расширения
и укажите степень расширения 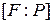 , если:
, если:
1) 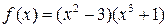 ,
, 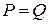 ;
;
2) 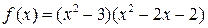 ,
, 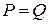 ;
;
3) 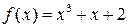 ,
, 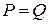 ;
;
4) 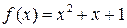 ,
, 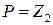 ;
;
5) 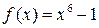 ,
, 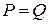 ;
;
6) 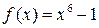 ,
, 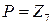 .
.
8.19. Докажите, что факторкольцо 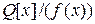 является полем, если:
является полем, если:
1) 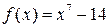 ;
;
2) 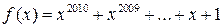 .
.
8.20. Напишите таблицы умножения для колец 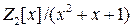 ,
, 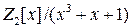 ,
, 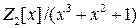 .
.
8.21. Пусть 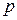 - простое число,
- простое число, 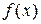 - многочлен с коэффициентами из
- многочлен с коэффициентами из 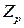 . Докажите, что
. Докажите, что 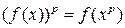 для любого
для любого 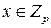 .
.
8.22. Разложите многочлен 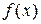 в произведение неприводимых над полем
в произведение неприводимых над полем 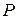 многочленов, если:
многочленов, если:
1) 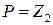 ,
, 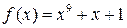 ;
;
2) 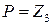 ,
, 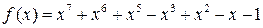 .
.
8.23. Докажите, что если 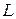 - расширение поля
- расширение поля 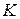 и степень расширения
и степень расширения 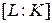 - простое число, то единственными полями
- простое число, то единственными полями 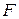 , удовлетворяющими условию
, удовлетворяющими условию 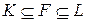 являются
являются 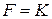 и
и 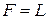 .
.
Шифрование.
Модулярным шифром называется отображение 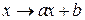 , где
, где 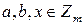 ,
, 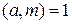 .
.
Различают следующие модулярные криптосистемы: криптосистема Рабина,RSA-криптосистема, криптосистема с открытым ключом, криптосистема без передачи ключей, протокол прямого обмена ключами (метод Диффи-Хеллмана), электронная цифровая подпись и пороговая система.
Криптосистема Рабина. Выбираются нечетные простые числа 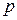 и
и 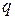 вида
вида 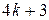 , (
, (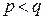 ). Они считаются секретными, а модуль
). Они считаются секретными, а модуль 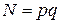 - несекретным. Функция шифрования задается формулой
- несекретным. Функция шифрования задается формулой 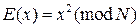 , где
, где 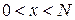 . Дешифрование сводится к решению сравнения
. Дешифрование сводится к решению сравнения 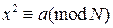 , которое распадается на четыре системы
, которое распадается на четыре системы 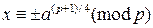 ,
, 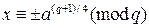 . Поскольку система Рабина применяется для шифрования осмысленного текста, то при дешифровании из четырёх возможных решений выбирается вариант, соответствующий осмысленному тексту.
. Поскольку система Рабина применяется для шифрования осмысленного текста, то при дешифровании из четырёх возможных решений выбирается вариант, соответствующий осмысленному тексту.
RSA-криптоситема. Пусть 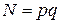 , где
, где 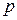 и
и 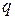 - большие простые числа. Модуль
- большие простые числа. Модуль 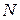 не является секретным, а числа
не является секретным, а числа 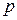 и
и 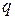 держатся в секрете. Число
держатся в секрете. Число 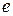 (открытый ключ) берется взаимно простым с
(открытый ключ) берется взаимно простым с 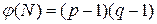 . Число
. Число 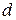 (секретный ключ) находится из условия
(секретный ключ) находится из условия 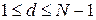 ,
, 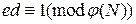 . При RSA-шифровании текст или его часть отождествляется с натуральным числом
. При RSA-шифровании текст или его часть отождествляется с натуральным числом 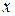 ,
, 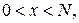
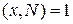 , а алгоритмы шифрования и дешифрования выглядят следующим образом:
, а алгоритмы шифрования и дешифрования выглядят следующим образом: 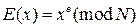 ,
, 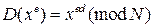 . RSA-криптосистему можно использовать и для цифровой подписи сообщения
. RSA-криптосистему можно использовать и для цифровой подписи сообщения 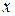 . Для этого обладатель секретного ключа вычисляет
. Для этого обладатель секретного ключа вычисляет 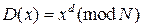 . Пара чисел
. Пара чисел 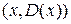 считается подписанным сообщением. Его подлинность можно проверить с помощью несекретного ключа
считается подписанным сообщением. Его подлинность можно проверить с помощью несекретного ключа 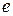 :
: 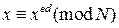 .
.
Дата публикования: 2015-11-01; Прочитано: 399 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
