 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм Евклида
|
|
ПРЕДИСЛОВИЕ
Курс прикладной алгебры, как раздел общего курса по геометрии и алгебре, читается на факультете прикладной математики и информатики на протяжении многих лет. Данный сборник задач является продолжением и дополнением к курсу лекций по данному предмету, поскольку здесь использован опыт проведения практических занятий. Содержание задачника соответствует программе курса.
Сборник состоит из десяти параграфов. Все десять параграфов условно можно разделить на три составные части: теория чисел (1 – 5), математические структуры (6 – 8), основы криптологии (9,10). В начале каждого параграфа приводятся некоторые определения и факты из теории, формулы и решения типичных примеров.
В конце сборника приведены ответы для практически всех представленных, с точки зрения авторов, наиболее трудных задач.
Каноническое разложение, НОД, НОК,
алгоритм Евклида.
Натуральное число n, большее единицы, называется простым числом, если его натуральными делителями являются лишь единица и само число n. Другие натуральные числа, большие единицы, называются составными.
Каноническим разложением натурального числа n, большего единицы, называется представление числа n в виде произведения примарных степеней 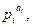 т.е.
т.е. 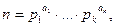 где
где 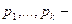 различные простые числа,
различные простые числа, 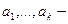 натуральные числа. Говорят, что простое число
натуральные числа. Говорят, что простое число 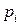 входит в каноническое разложение
входит в каноническое разложение 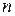 с показателем
с показателем 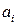 , и пишут
, и пишут 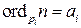 . Каноническое разложение натурального числа существует и притом единственно с точностью до порядка следования множителей.
. Каноническое разложение натурального числа существует и притом единственно с точностью до порядка следования множителей.
Пусть 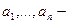 целые числа, не равные нулю.
целые числа, не равные нулю.
Целое число d называется общим делителем чисел 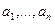 , если число d делит эти числа. Наибольшим общим делителем (НОД) чисел
, если число d делит эти числа. Наибольшим общим делителем (НОД) чисел 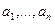 называется натуральное число D такое, что числа
называется натуральное число D такое, что числа 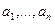 делятся на D, причем D само делится на любой другой общий делитель чисел
делятся на D, причем D само делится на любой другой общий делитель чисел 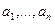 . Наибольший общий делитель чисел
. Наибольший общий делитель чисел 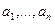 обозначается НОД{
обозначается НОД{ 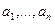 } или (
} или (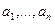 ).
).
Целое ненулевое число k называется общим кратным чисел 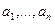 , если число к делится на эти числа. Наименьшим общим кратным (НОК) чисел
, если число к делится на эти числа. Наименьшим общим кратным (НОК) чисел 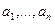 называется натуральное число К такое, что число К делится на числа
называется натуральное число К такое, что число К делится на числа 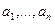 , причем любое общее кратное чисел
, причем любое общее кратное чисел 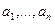 делится на К. Наименьшее общее кратное чисел
делится на К. Наименьшее общее кратное чисел 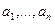 обозначается НОК{
обозначается НОК{ 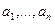 } или [
} или [ 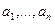 ].
].
Если известны представления натуральных чисел а и b в виде произведения примарных степеней, а именно, 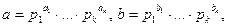 то
то 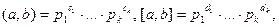 где
где 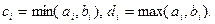 В частности,
В частности, 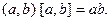
Для нахождения НОД и НОК верны следующие соотношения: 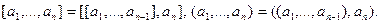
Пусть a, b – целые не нулевые числа, тогда существует единственная пара целых чисел q, r такая, что 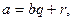 причем
причем 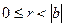 (теорема о делении с остатком).
(теорема о делении с остатком).
Кроме указанного выше метода нахождения наибольшего общего делителя двух чисел, который использует их каноническое разложение, наибольший общий делитель можно найти также с помощью алгоритма Евклида. Для этого число а разделим на b с остатком: 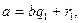 где
где 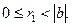 Если
Если 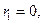 то
то 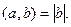 Если
Если 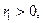 то разделим b на
то разделим b на 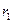 с остатком:
с остатком: 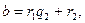 где
где 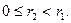 Если
Если 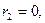 то
то 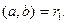 Если
Если 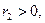 то разделим
то разделим 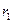 на
на 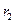 с остатком:
с остатком: 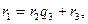 где
где 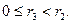 И так далее продолжаем эту процедуру. Конечный не нулевой остаток и будет наибольшим общим делителем чисел a и b.
И так далее продолжаем эту процедуру. Конечный не нулевой остаток и будет наибольшим общим делителем чисел a и b.
С помощью алгоритма Евклида наибольший общий делитель чисел 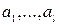 можно представить в виде линейной комбинации этих чисел, а именно, существуют целые числа
можно представить в виде линейной комбинации этих чисел, а именно, существуют целые числа 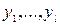 такие, что НОД
такие, что НОД 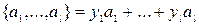 . Такое представление называется линейным разложением наибольшего общего делителя чисел
. Такое представление называется линейным разложением наибольшего общего делителя чисел 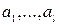 .
.
Числа 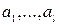 называются взаимно простыми, если
называются взаимно простыми, если 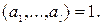 Числа
Числа 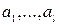 называются попарно взаимно простыми, если
называются попарно взаимно простыми, если 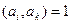 для любых
для любых 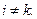
Сформулируем некоторые свойства взаимно простых чисел:
1) если ab делится на с, 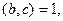 то а делится на с;
то а делится на с;
2) 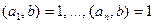 тогда и только тогда, когда
тогда и только тогда, когда 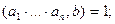
3) 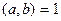 тогда и только тогда, когда
тогда и только тогда, когда 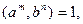 где m, n – натуральные числа.
где m, n – натуральные числа.
Пример 1. Найдите наибольший общий делитель 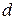 и наименьшее общее кратное чисел 8633 и 7387, а также найдите целые числа
и наименьшее общее кратное чисел 8633 и 7387, а также найдите целые числа 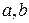 , такие, что
, такие, что 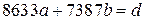 .
.
Решение. Воспользуемся алгоритмом Евклида. Последовательно произведем следующие деления с остатком: 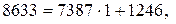
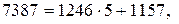
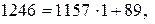
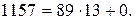 Следовательно,
Следовательно,
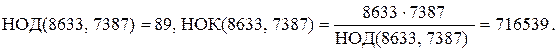
Найдем линейное разложение наибольшего общего делителя. Так как 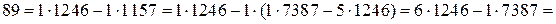
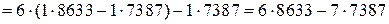 ,то
,то 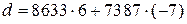 - искомое линейное разложение наибольшего общего делителя.
- искомое линейное разложение наибольшего общего делителя.
Пример 2. Определите, сколькими нулями оканчивается число 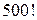 .
.
Решение. Так как число нулей, которыми оканчивается число 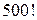 есть максимальная степень 10, на которую делится
есть максимальная степень 10, на которую делится 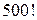 ,
, 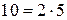 , то искомое число нулей равно
, то искомое число нулей равно 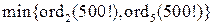 . Очевидно,
. Очевидно,
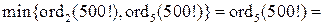
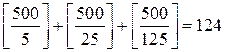 (см. задачи № 1.11, 1.12).
(см. задачи № 1.11, 1.12).
1.1. Найдите канонические разложения чисел:
1) 16 900, 2) 60 480, 3) 555 555, 4) 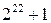 , 5)
, 5) 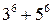 .
.
1.2. Докажите, что если натуральное число n, большее 1, не делится ни на
одно простое число, не превосходящее 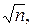 то число n является простым.
то число n является простым.
1.3. Какие из следующих чисел являются простыми: 161, 1001, 1087,
1357, 2011, 11111?
1.4. (Евклид) Докажите, что существует бесконечно много простых чисел.
1.5. Докажите, что существует бесконечно много простых чисел вида:
1) 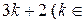 N), 2)
N), 2) 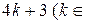 N), 3)
N), 3) 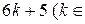 N).
N).
1.6. Пусть n – натуральное число. Докажите, что существует натуральное число m, такое что числа 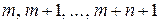 являются составными.
являются составными.
1.7. Пусть m, n – натуральные числа, большие 1.
1) (Жермен) Докажите, что число 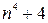 является составным.
является составным.
2) Докажите, что число 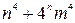 является составным.
является составным.
1.8. 1) Пусть n – натуральное число, большее 4. Докажите, что число n является простым тогда и только тогда, когда 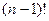 не делится на n.
не делится на n.
2) (Вильсон) Пусть n – натуральное число. Докажите, что число n является простым
тогда и только тогда, когда 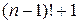 делится на n.
делится на n.
1.9. 1) Докажите, что число 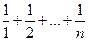 не является натуральным при
не является натуральным при 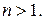
2) Докажите, что число 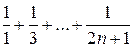 не является натуральным для любого
не является натуральным для любого 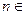 N.
N.
1.10. Докажите, что для любого натурального значения n произведение 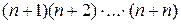 делится на
делится на 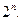
1.11. Пусть [ x ] обозначает наибольшее целое число, не превосходящее х. Докажите, что 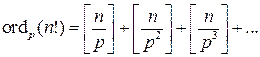 для любого натурального
для любого натурального 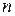 и любого простого
и любого простого 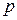 .
.
1.12. 1) Сколькими нулями оканчивается число 2011!
2) Найдите максимальную степень, в которой число 21 входит в разложение числа 2011!
1.13. Вычислите наибольшие общие делители c помощью алгоритма Евклида и найдите их линейные разложения:
1) (187, 221), 2) (6188, 4709), 3) (2419, 1189, 1711), 4) (549, 387),
5) (78, 60, 24).
1.14. Вычислите наименьшие общие кратные:
1) [1189, 2419, 1711], 2) [6408, 9256, 4272], 3) [551, 899],
4) [549, 387], 5) [78, 60, 24].
1.15. Пусть 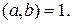 Докажите, что
Докажите, что
1) 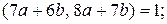 2)
2) 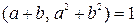 либо 2.
либо 2.
1.16. Найдите наибольшее возможное число шагов алгоритма Евклида для двух трёхзначных чисел.
1.17. Докажите, что для любого натурального 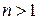 отрезок
отрезок 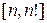 содержит простое число.
содержит простое число.
1.18. Докажите, что для любых натуральных 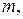
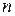 (
(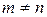 ) числа Ферма
) числа Ферма 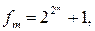
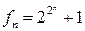 взаимно просты.
взаимно просты.
1.19. Пусть 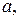
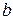 - натуральные взаимно простые числа, произведение которых является точным квадратом. Докажите, что числа
- натуральные взаимно простые числа, произведение которых является точным квадратом. Докажите, что числа 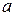 и
и 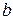 являются точными квадратами.
являются точными квадратами.
1.20. Докажите, что если квадрат рационального положительного числа 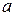 является натуральным числом, то число
является натуральным числом, то число 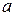 натуральное.
натуральное.
1.21. Существует ли многочлен с целыми коэффициентами от целой переменной, значениями которого могут быть только простые числа или им противоположные?
1.22. Найдите все натуральные 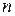 , такие, что
, такие, что 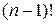 не делится на
не делится на 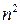 .
.
1.23. Найдите все натуральные 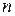 , для которых
, для которых 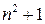 делится на
делится на 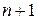 .
.
1.24. Докажите, что 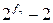 делится на
делится на 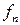 для любого натурального
для любого натурального 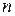 .
.
1.25. Докажите, что существует бесконечно много нечётных натуральных 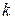 , для которых все числа
, для которых все числа 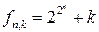 (
(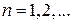 ) являются составными.
) являются составными.
1.26. Докажите, что 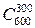 делится на 7, а
делится на 7, а 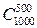 - нет.
- нет.
Дата публикования: 2015-11-01; Прочитано: 1162 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
