Корень многочлена

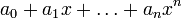
над полем k — элемент 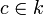, который после подстановки его вместо x обращает уравнение

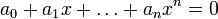
в тождество.

• Если c является корнем многочлена p (x), то p (x) делится без остатка на x − c (теорема Безу).
• Число вещественных корней многочлена с вещественными коэффициентами степени n заведомо меньше либо равно n. При этом комплексные корни многочлена (если они есть) сопряжены, таким образом, многочлен четной степени может иметь только четное число вещественных корней, а многочлен нечётной — только нечётное.
• Всякий многочлен p (x) с вещественными или комплексными коэффициентами имеет, по крайней мере, один, вообще говоря, комплексный корень (основная теорема алгебры).
• То же верно для любого алгебраически замкнутого поля.
• Более того многочлен p (x) можно записать в виде

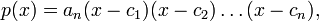
где 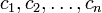— (в общем случае комплексные) корни многочлена p (x), возможно с повторениями, при этом если среди корней 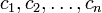многочлена p (x) встречаются равные, то общее их значение называется кратным корнем.

• Корни многочлена связаны с его коэффициентами формулами Виета

Теорема тождественности

В сложный анализ, теорема тождественности для голоморфные функции положения: дали функции f и g голоморфно на a соединено открытого множество D, если f = g на некотором районе z то внутри D, после этого f = g на D. Таким образом голоморфная функция вполне обусловлена своими значениями на районе a (по возможности довольно малого) внутри D. Это не поистине для реальн-differentiable функций. В сравнении, голоморфностью, или сложным-differentiability, будут очень более твердая придумка. Неофициально, иногда суммировать теорему путем говорить голоморфные функции «трудно» (в отличие от, мнение, непрерывные функции которые «мягки»).

Underpinning факт от теорема установлено developability голоморфной функции в свою серию портноя.

Доказательство

Предположение connectedness на домене D будет обязательно и будет в действительности ключево к скоро доказательству, котор дали здесь. (Очевидно если D consist of 2 disjoint открытого множество, результат не держит.) под этим предположением, в виду того что мы даемся что комплект не пуст, топологически сумма иска к тому f и g совпадите на комплекте оба открыто и закрыто. Closedness немедленно от непрерывность f и g.

Поэтому главный вопрос должен показать что комплект на f = g совпадите на открытого множество. Потому что голоморфная функция может быть представлена своим Серия портноя везде на своем домене, достаточно рассматривать комплект

Предположите w лож внутри S. После этого, потому что серия портноя f и g на w имейте non-zero радиус схождения, открытый диск B_r (w) также лежит внутри S для некоторого r. (В действительности, r может быть что-нибыдь чем расстояние от w к границе D). Это показывает S будет открыто и доказывает теорему.

Алгебраически замкнутое поле — поле 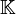, в котором всякий многочлен ненулевой степени над 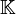имеет хотя бы один корень.

Для любого поля существует единственное с точностью до изоморфизма его алгебраическое замыкание, то есть его алгебраическое расширение, являющееся алгебраически замкнутым.

Основна́я теоре́ма а́лгебры утверждает, что

Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.

Эквивалентная формулировка теоремы следующая:

Поле комплексных чисел алгебраически замкнуто.

Следствие

Немедленным следствием из теоремы является то, что любой многочлен степени 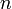над полем комплексных чисел имеет в нём ровно 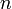корней, с учётом кратности корней.

Доказательство.

У многочлена 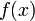есть корень 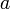, значит, по теореме Безу, он представим в ви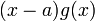де , где 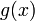— другой многочлен. Применим теорему к 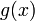и будем применять её таким же образом до тех пор, пока на месте 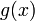не окажется линейный множитель.

Доказательство.

Представим полином 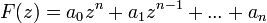в виде суммы 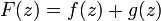, где 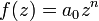, 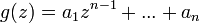. Составим соотношение 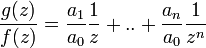. Легко видеть, что для любых коэффициентов 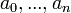всегда найдется такое значение 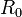, что для всех значений 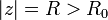имеет место неравенство 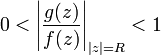. В силу теоремы Руше следует, что полное число нулей функции 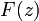в круге 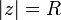равно числу нулей в этом круге функции 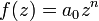. Но функция 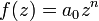на всей комплексной плоскости имеет один единственный n-кратный корень 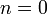. Отсюда, в силу произвольности 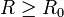и следует утверждение теоремы.

Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.