 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Энтропия как критерий максимального правдоподобия
|
|
(моделирование по принципу статистического вывода)
Цель практического занятия, показать каким образом можно найти решение задачи, используя информационную энтропию в качестве критерия максимального правдоподобия, если мы имеем достоверную, но недостаточную исходную информацию о системе.
На уровне описания процесса (системы) информационная энтропия используется как критерий правдоподобия. Рассмотрим применение данного метода на примере испарения многокомпонентной смеси.
Задача. Пусть имеется 1 моль многокомпонентной смеси в однофазном и двухфазном состоянии состава zi. Смесь нагревается до температуры Т (T1< Т< Т2) при давлении Р и расслаивается на две фазы (жидкость и пар). Требуется найти при заданном Р и Т состав пара yi, состав жидкости xi, доли пара g и жидкости l. Введем обозначения:
yi – мольная доля i -го компонента в паровой фазе 

xi – мольная доля i -го компонента в жидкой фазе 
T1 – температура начала кипения смеси;
Т2 – температура окончания кипения смеси;
m – количество компонентов смеси.
Многокомпонентная смесь имеет интервал температур начала T1 и окончания кипения жидкости Т2.
Постановка задачи. Найти наиболее вероятное распределение компонентов между фазами в процессе перехода от начального к конечному (равновесному) состоянию. Составим исходную систему уравнений применительно к данной системе. Уравнение материального баланса для i -го компонента:
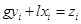 ,
,  ,
,  (1)
(1)
где gyi – относительная доля i -го компонента в паровой фазе;
l xi – относительная доля i -го компонента в жидкой фазе.
Уравнений материального баланса можно записать столько, сколько компонентов содержит исходная смесь, а именно m уравнений.
Запишем уравнения нормировки

 (2)
(2)
 (3)
(3)
Здесь и далее индекс i у знака Σ будем опускать. Зададим состояние фаз средним значением некоторой функции. Свойства компонентов введем через усредненные свойства:


 , (4)
, (4)
где 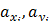 – параметры, оценивающие характерные свойства компонентов;
– параметры, оценивающие характерные свойства компонентов;
 – средние значения характерных свойств компонентов.
– средние значения характерных свойств компонентов.
Уравнения (1) - (4) образуют исходную систему уравнений. Общее число уравнений составляет m+3, что, однако, меньше числа неизвестных g, l, уi, хi  . Уравнений (1) - (4) недостаточно, чтобы получить искомые величины даже для простейшего случая m=2 (бинарная месь), т.к. 2m+2 > m+3 для m>2. Получена незамкнутая система уравнений, в которой, чем больше m, тем больший разрыв между количеством уравнений и количеством неизвестных. И, тем не менее, для подобной задачи можно сформулировать решение, если воспользоваться информационным принципом максимальной энтропии. Согласно этому принципу энтропия может быть использована как критерий правдоподобия, так что наиболее вероятными (правдоподобными) значениями искомых величин будут такие, которые соответствуют максимальной неопределенности системы.
. Уравнений (1) - (4) недостаточно, чтобы получить искомые величины даже для простейшего случая m=2 (бинарная месь), т.к. 2m+2 > m+3 для m>2. Получена незамкнутая система уравнений, в которой, чем больше m, тем больший разрыв между количеством уравнений и количеством неизвестных. И, тем не менее, для подобной задачи можно сформулировать решение, если воспользоваться информационным принципом максимальной энтропии. Согласно этому принципу энтропия может быть использована как критерий правдоподобия, так что наиболее вероятными (правдоподобными) значениями искомых величин будут такие, которые соответствуют максимальной неопределенности системы.
В качестве меры неопределенности используем информационную энтропию (п. 1.3, форм. (10))
 (5)
(5)
Энтропия (5) характеризует меру неопределенности состава фазы. В соответствии с принципом максимального правдоподобия, самое достоверное решение может быть получено при max информационной энтропии
 , (5*)
, (5*)
где 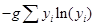 – мера неопределенности паровой фазы,
– мера неопределенности паровой фазы,  ;
;

 – мера неопределенности жидкой фазы,
– мера неопределенности жидкой фазы,  .
.
Решение задачи. Формально задача сводится к решению условной экстремальной задачи: требуется найти такие значения параметров g, l, уi, хi  , которые отвечали бы максимальному значению энтропии (5*) при соблюдении ограничений (1) - (4), т.е. из множества решений требуется найти одно, наиболее вероятное.
, которые отвечали бы максимальному значению энтропии (5*) при соблюдении ограничений (1) - (4), т.е. из множества решений требуется найти одно, наиболее вероятное.
Этап 1. Применяя метод неопределенных множителей Лагранжа, переводим условную экстремальную задачу в безусловную экстремальную. (Для этой цели вводится специальная функция Лагранжа F, которая переводит условную экстремальную задачу в класс безусловных экстремальных задач).
Переходим к замкнутой системе уравнений:

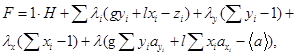
где λi, λy, λx, λ – множители Лагранжа
F -функция Лагранжа.
Функция Лагранжа – многочлен, включающий целевую функцию (5) и ограничения (1) - (4). Необходимое условие экстремальности: равенство нулю частных производных функции Лагранжа по неизвестным параметрам.

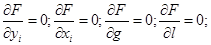
Найдем частные производные:
 (6)
(6)
 (7)
(7)
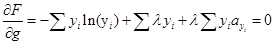 (8)
(8)
 (9)
(9)


В полученной замкнутой системе количество уравнений (3 m +5)равно количеству неизвестных
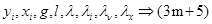
Этап 2. Решение замкнутой системы алгебраических уравнений.
Из уравнения (6) выразим ln(yi) и полученное выражение (10) подставим в уравнение (8):
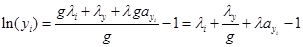 (10)
(10)
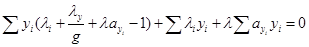

Получаем 

Из уравнения (7) выразим ln(xi) и полученное выражение (11) подставим в уравнение (9):
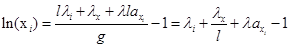 (11)
(11)
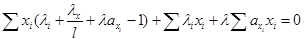


Получаем 
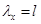
Подставляем λy в выражение (10) и λx в выражение (11):

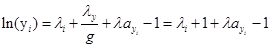

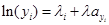 (12)
(12)


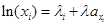 (13)
(13)
или:

 (12*)
(12*)
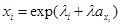 (13*)
(13*)
Подставляем (12*)и(13*)в уравнение (1):

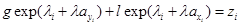
и преобразуем 

Освободимся от множителя Лагранжа. Подставим выражение для 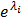 в выражения (12*) и (13*):
в выражения (12*) и (13*):

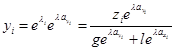
Разделим числитель и знаменатель на  :
:

 (14)
(14)


Разделим числитель и знаменатель на 

 (15)
(15)
Этап 3. Идентификация коэффициентов  ,
, 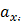 .
.
Поскольку конечные выражения содержат параметры  ,
, 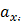 , только в виде разности, то выбор начала отсчета для них не имеет значения. Разделив (12*)на (13*), можно убедиться, что уравнение переходит в тождество:
, только в виде разности, то выбор начала отсчета для них не имеет значения. Разделив (12*)на (13*), можно убедиться, что уравнение переходит в тождество:

Известно, что для равновесного состояния системы справедливо соотношение:
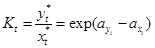 , (16)
, (16)
где Ki – константа фазового равновесия. Знак (*) обозначает принадлежность к равновесному состоянию.
Сравнивая два последних выражения, заключаем, что для равновесного состояния λ=1.
Из выражения (16):

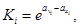
откуда:

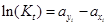 (17)
(17)
Константа фазового равновесия Кi (17) пропорциональна работе, которую необходимо совершить при переходе вещества из одной фазы в другую.
Этап 4. Получение расчетных формул. Подставим выражение (17)в(14)и(15):


 (18)
(18)

 (19)
(19)
Подставим в выражение (18) l=1-g, т.к. l+g=1


Подставляем уравнение (18) в (2):

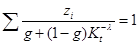 (20)
(20)

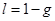
Формулы (18) - (21) представляют собой решение поставленной задачи. Таким образом, уравнения (18) - (21) позволяют найти наиболее вероятные распределения компонентов между фазами. При этом роль координаты процесса выполняет множитель Лагранжа.
Алгоритм решения задачи
Пусть некоторую смесь заданного состава zi, нагреваем до температуры Т. Смесь находится в равновесии (пар-жидкость). Для равновесного состояния принимаем λ =1. При заданных параметрах (температуре Т и давление Р) рассчитываем по экспериментальным данным константу фазового равновесия Kf.
В уравнении (20) только один неизвестный параметр: доля пара g. Из уравнения (20) вычисляем g, а по формуле (21) определяем долю жидкости l. По формулам (18) и (19) рассчитываем все концентрации yi и xi.
Таким образом, математические выражения (18)-(21) позволяют найти наиболее вероятные распределения компонентов между паровой и жидкой фазами для процесса испарения многокомпонентной смеси.
Информационный принцип максимального правдоподобия позволяет находить решение задачи при неполной, но достоверной информации. И это лучше, чем дополнить субъективной информацией.
Основные обозначения:
Н – информационная энтропия, мера неопределенности, мера разнообразия, бит;
I – количество информации, блокированное разнообразие, бит;
k – количество исходов опыта;
p – вроятность исхода опыта;
η – критерий степени оценки организованности системы;
S – термодинамическая энтропия, Дж/К;
W — число микросостояний системы (термодинамическая вероятность);
xi – мольная доля i -го компонента в жидкой фазе (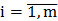 );
);
yi – мольная доля i -го компонента в паровой фазе (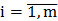 );
);
zi – состав сырья (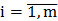 );
);
m – число компонентов в смеси;
g – доля пара;
l – доля жидкости;
λi, λy, λx, λ – множители Лагранжа;
Ki – константа фазового равновесия (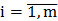 );
);
kB – постоянная Больцмана, 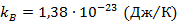 ;
;
Дата публикования: 2015-10-09; Прочитано: 354 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
