Связь информационной энтропии с энтропией

статистической физики (термодинамической энтропией)

Цель практического занятия: усвоить физический смысл энтропии, показать аналогию между термодинамической и информационной энтропией на примере энтропии идеального газового состояния.

Рассмотрим, как согласуется понятие информационной энтропии с понятием энтропии в термодинамике, занимающейся изучением состояния макроскопических объектов. Статисти­ческая термодинамика основана на атомно-молекулярных представлениях и ее основную задачу можно сформулировать таким образом: зная законы поведения частиц на микроуровне, установить законы поведения макроскопического количества вещества. Для этого выясним, какие распределения частиц возможны. При этом будем различать изменения микро- и макросостояния системы. Если произошло изменение числа частиц на каком-либо энергетическом уровне, то будем говорить об изменении макросостояния системы. Если же произойдет обмен частиц между энергетическими уровнями, но распределение частиц по уровням энергии осталось прежним, будем фиксировать изменение микросостояния системы. Таким образом, одно макросостояние системы может быть реализовано очень многими микросостояниями.

Рассмотрим связь термодинамической энтропии с информа­ционной. Согласно закону Больцмана термодина­мическая энтропия пропорциональна логарифму числа микро­состояний

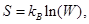(1)

где k_B – постоянная Больцмана.

;

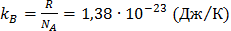R – газовая постоянная, R=8314 (Дж/кмоль×К);
N_А – число Авогадро, N_А=6,06×10²⁶(кмоль^-1);
W – число микросостояний (термодинамическая вероятность);
S – термодинамическая энтропия (кДж/К).

Согласно соотношению Клаузи

,

где Q – количество тепла (кДж);
T – температура (К).

Температура в термодинамике характеризует средне­статистическую кинетическую энергию частиц на макроуровне. Согласно второму началу термодинамики энтропия закрытой системы может только повышаться, что означает увеличение числа возможных микросостояний.

Если воспользоваться информационной энтропией для оценки неопределенности, связанной с определением того микро­состоя­ния, в котором находится система в данный момент, то принимая во внимание, что все микросостояния равновероятны, получаем согласно формуле (4), (разд. 1.1)

(2)

Сравнивая выражения (1) и (2) отметим их сходство. Они отличаются лишь на постоянный множитель, что для информационной энтропии не имеет принципиального значения (напомним, что информационная энтропия определяется с точностью до множителя). Размерность термодинамической энтропии Дж/К, в известной мере, условна. Размерность S связана исключительно с использованием температурной шкалы для оценки степени нагретости тела. Если температуру измерять в Дж (использовать энергетическую шкалу), тогда термодинамическая энтропия станет безразмерной величиной.

Для того, чтобы понять существо статистических методов, рассмотрим в качестве примера идеальный газ, состоящий из достаточно большого числа молекул, находящийся в равновесии. При фиксированных давлении Р и температуре Т система имеет определенное распределение частиц по энергиям (с точки зрения молекулярной физики мы зададим систему на макроуровне).

Пусть общее число частиц в системе – N, которые распределены на макроуровне следующим образом:

N₁ – число частиц с энергией ε₁ на первом макроуровне;
N₂ – число частиц с энергией ε₂ на втором макроуровне;
……………………
N_i – число частиц с энергией ε_i (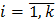) на i -ом макроуровне;
……………………
N_k – число частиц с энергией ε _к на k-ом макроуровне;
k – количество макроуровней энергий.

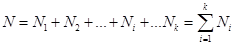
Вероятность обнаружения частицы с энергией ε_i, на макроуровне равна .

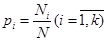Число возможных перестановок (микросостояний системы) для каждого макроуровня W рассчитывается по формуле

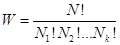(3)

Для того, чтобы показать аналогию между термоди­намической и информационной энтропией не только для равновероятных событий, но и для общего случая (разд. 1.1, форм.(7)), раскроем значение W (3), предварительно прологарифмировав его.

Выражение (2) с учетом (3) запишем в следующем виде:

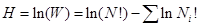
Используя формулу Стирлинга, избавляемся от фактериалов:

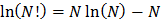
Тогда

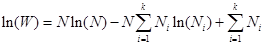
Заметив, что 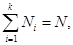а

Получим

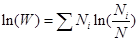
Умножив обе части этого выражения на k_B/N и полагая, что вероятность обнаружить частицу на i -ом энергетическом уровне равна 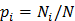, получим

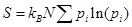(4)

Таким образом, получаем выражение (4) аналогичное информационной энтропии (разд. 1.1, форм.7):

Сравним информационную и термодинамическую энтропию. Информационная энтропия Н – безразмерная величина, в то время как термодинамическая энтропия S – размерная величина и, как было сказано выше, размерность термодинамической энтропии (Дж/К) - это историческая случайность.

Поскольку понятие энтропии в информации не связывается с каким-либо определенным типом неупорядоченности, то в этом смысле оно является более широким, чем понятие энтропии в термодинамике. Когда речь идет о термодинамической энтропии, то всегда имеется в виду неупорядоченность, связанная с хаотическим тепловым движением молекул. Термодинамическая энтропия привязана к одному типу неупорядоченности. При этом способ оценки неупорядоченности (через логарифмы вероятности) в термодинамике и теории вероятности остается одним и тем же. Получив формулу (1) для расчета термодинамической энтропии в 1877 году Л.Больцман обронил фразу о том,, что «энтропия характеризует недостающую информацию». Тогда этой фразы никто не понял, но она оказалась пророческой: в настоящее время информация рассматривается как фундаментальное свойство материи.

Для того, чтобы понять существо статистических методов, проследим на упрощенной модели, как появляются свойства, связанные с понятием термодинамической энтропии.

Пример. Рассмотрим систему из десяти частиц (N =10), распределенных на четырех энергетических уровнях (k =4), имеющих относительные величины энергии: ε₁ =l, ε ₂ = 2, ε ₃ = 3, ε ₄ = 4. Общая энергия системы равна двадцати относительным единицам (Е =20). Задача заключается в том, чтобы найти то состояние, которое примет система, предоставленная самой себе, т.е. относительно того, как распределятся частицы по уровням энергии. Понятия макро- и микросостояния вам известны.

Так одно из возможных макросостояний десяти частиц следующее: три частицы располагаются на энергетическом уровне 1 (N ₁=3), пять частиц располагаются на энергетическом уровне 2 (N ₂=5), и по одной частице на энергетических уровнях 3 и 4 (N ₃=l, N ₄=1).

Общая энергия E = Σε_iN_i =3∙1+5∙2+1∙3+1∙4=20.Проведем мысленный эксперимент: введем маркировку частиц A,B,C,D,... (табл.1). Тогда данное макросостояние можно обеспечить через различные микросостояния, осуществляя разные перестановки частиц. Микросотояние 2: частица D перейдет на энергетический уровень 2, а частица С перейдет на энергетический уровень 1. Микросотояние 3: частицы G и С поменяли энергоуровни и т.д.

Число возможных перестановок частиц на микроуровне рассчитываем по формуле (3)

т.е. для рассматриваемого макросостояния возможно 5040 микросотояний.

Таблица 1

Уровни частиц	ε1 =l	ε 2=2	ε 3 = 3	ε 4=4	Примечание
Макросостояние					N= 10.
					ΣεiNi=20
Микросостояние №1	А, В, С	D, Е, К, L, М	N	G
Микросостояние №2	A, B, D	С, Е, К, L, М	N	G
Микросостояние №3	А, В, D	С, Е, К, L, М	G	N

На практическом занятии необходимо найти все возможные макросостояния рассматриваемой системы и рассчитать для каждого макросостояния системы число микросостояния.

Рассчитать возможное число микросостояний 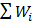и вероятность макросостояния т.е., 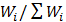. Результаты расчетов представить в виде таблицы, расположив их в порядке возрастания числа микросостояний. Выделить макросостояние системы с наибольшим числом микросостояний. Важно отме­тить, что только одному макросостоянию будет принад­лежать максимальное число микросостояний. Следовательно, если вероятность пребывания системы в любом микросостоянии одинакова, то вероятность пребывания системы в том или ином макросостоянии оказывается различной и тем большей, чем больше способов осуществления данного макросостояния.

Анализ показывает, что если число частиц станет очень большим и возрастет число энергетических уровней (как это имеет место в реальных системах), то всегда есть одно макросостояние, для которого число микросостояний будет значительно преобладать над остальными. Например, 99,9% всех возможных микросостояний может принадлежать одному макросостоянию.

Таблица 2

. Распределение частиц по уровням

Номер макросостояния системы j	Уровни энергии	Число микросостояний Wj	Число микросостояний в %
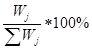
ε1 =l	ε 2=2	ε 3 = 3	ε 4=4
	..	..	..	..	..
j	..	..	..	..	..
..	..	..	..	..	..
..	..	..	..	..	..
..	..	..	..	..	..
Всего		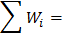	100,0

Из вышесказанного можно сделать следующее заключение: если реальная система предоставлена сама себе, она стремится занять состояние с максимальной энтропией.