Энтропия и информация в системном анализе

Суркова Л.В.

С90Теория системного анализа: Учебное пособие /Л.В. Суркова,

Н.Г. Мишина – М.: Университет машиностроения, 2013. – 46 с.

В учебном пособии изложены теоретические основы сис­темного анализа: информационная энтропия и количество информации.

Предназначено студентам 3–4 курсов при изучении теоретического курса учебных дисциплин «Системный анализ», «Системный анализ процессов химической технологии», «Теория системного анализа и принятия решения» дневной и очно-заочной форм обучения по направлениям подготовки: 241000.62 «Энерго- и ресурсосберегающие процессы химии­ческой технологии, нефтехимии и биотехнологии», 280700.62 «Техносферная безопасность», 240700.62 «Биотехнология» и др.

УДК 007: 66.0

ББК 34.455

© Л.В. Суркова, Н.Г.Мишина, 2013

© Университет машиностроения, 2013

Энтропия и информация в системном анализе

Современное понимание информации и ее роль в искусственных и’ естественных системах сложилось не сразу. Информация - это совокупность знаний, полученных разными науками: физикой, биологией, философией, теорией связи и т.д.

С другой стороны к этой проблеме пришла философская теория познания. Признав, что наше знание есть отражение реального мира, материалистическая теория познания установила, что отражение является всеобщим свойством материи. Сознание человека является специфической формой отражения.

Как только состояние одного объекта находится в соответствии с состояниями другого объекта, мы говорим, что один объект отражает другой, содержит информацию о другом (положение стрелки вольтметра и напряжение на его клеммах; соответствие между нашими ощущениями и реальностью).

В настоящее время информация рассматривается как фундаментальное свойство материи. Понятие информации столь же фундаментально для всей системологии как и понятие энергии для физики.

Исследуя информацию, кибернетика не открыла нового свойства материи: оно известно в философии под названием свойства отражения. Новое состоит в том, что информацию можно исследовать количественно.

1.1. Энтропия дискретного множества.

Понятие неопределенности

В системном анализе теоретическим ядром являются понятия энтропия и количество информации. Энтропия высту­пает как мера неопределенности. Характер неопре­делен­ности может быть самым различным, например:

- неопределенность типа незнания (являемся ли мы единст­венными во Вселенной; есть ли жизнь на Марсе и т.д.) со временем узнаем;

- неопределенность типа расплывчатости (древние философы дискутировали вопрос о том, сколько песчинок должно быть собрано вместе, чтобы получилась куча песка; в математике - теория расплывчатых множеств);

- неопределенность статистического типа (неопределенность содержания ожидаемого сообщения или события, неопределенность состояния системы).

Неопределенность статистического типа можно свести к теории вероятности и измерить. Введем количественную меру для данного типа неопределенности.

Сосредоточим внимание на сущности неопределенности и рассмотрим несколько простейших опытов, которые обозначим А, Б и В.

Введем характеристики опыта:

k – число исходов опыта;

Р_i – вероятность i -го исхода опыта (i = );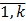

Н – мера неопределенности результата опыта

Опыт А будет заключаться в подбрасывании монеты. В этом опыте возможны два исхода (k=2). Монета упала гербом вверх, либо вниз. Вероятность каждого исхода .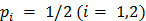

Опыт Б - подбрасывание игральной шестигранной кости. В этом опыте возможны шесть исходов (k =6). Вероятность каждого исхода .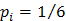
()

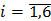Опыт В предполагает одновременное подбрасывание двух игральных костей. Для этого опыта 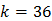и .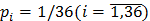

Оценка неопределенности результатов этих опытов есть оценка трудности угадывания исходов опытов. Интуитивно ясно, что из всех описанных опытов опыт В имеет максимальную неопределенность, поскольку число исходов здесь самое большое и заранее предвидеть исход этого опыта труднее всего. Чтобы перейти к количественной оценке неопределенности, сформулируем основные требования к функции, которая должна выполнять роль меры неопре­делен­ности Н.

Так как любая теория строится на аксиоматике, постулируем:

1. Значение Н монотонно возрастающая функция при увеличении числа исходов опыта, ;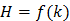

2. Значение 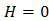, если опыт имеет единственный исход (k 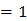). Это означает, что никакой неопределенности не возникает и результат опыта очевиден;

3. Неопределенность двух опытов Б следует рассматривать как неопределенность одного опыта В, т.е. суммарное значение энтропии двух опытов Б равно энтропии опыта В. Нельзя утверждать, что это два опыта Б или один опыт В, т.к. ситуация неразличима. Оценка неопределенности обладает свойством аддитивности. Это положение следует из того, что эти две ситуации физически неразличимы. По умолчанию мы принимаем, что вероятность каждого исхода опыта одинакова.

,

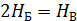где 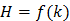– неопределенность опыта Б;
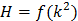– неопределенность опыта В;
k – число исходов опыта Б.

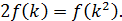
В общем виде для п простых опытов можно записать:

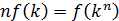
(1)

Функциональное уравнение (1) можно решить относительно функции 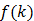. Дифференцируем выражение (1) по k, используя свойство монотонности функции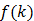

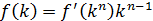
(2)

Далее дифференцируем выражение (1) по n

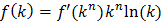
(3)

Разделим уравнение (2) на (3)

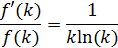
Или

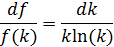
Интегрируя, находим:

,

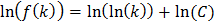где 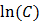– постоянная интегрирования.

Из последнего выражения следует

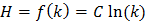
Получено простое решение уравнения (1), но С определить нельзя, так как нет необходимой информации для отыскания постоянной интегрирования.

Так как с увеличением k энтропия растет, то С >0, и последнее выражение можно переписать в окончательном виде:

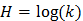
(4)

Из этого выражения видно, что оно удовлетворяет второму исходному постулату.

Выбор основания логарифма не имеет значения и определяет лишь выбор единицы измерения неопределенности. В теории информации обычно используется двоичный логарифм, в термодинамике – натуральный логарифм. Мера неопределенности Н определяется с точностью до множителя.

Итак, при k равновероятных исходах неопределенность опыта составляет:

,

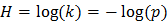(4*)

где 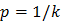– вероятность исхода опыта.

Если учесть, что для равновероятных исходов

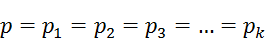
то умножая (4*) на единицу в виде 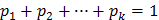, получим

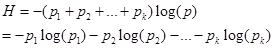(5)

Каждый член правой части выражения (5) можно рассматривать как вклад отдельного исхода в общую неопределенность опыта. В случае равновероятных исходов вклад каждого исхода одинаков.

Если предположить, что некоторые исходы опытов менее вероятны, чем другие, в таком случае можно говорить о средней неопределенности опыта. Мы пришли к той же форме записи (5), только теперь предполагается, что вклад каждого исхода в общую неопределенность опыта необязательно одинаков.

Например: 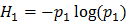— вклад первого исхода в общую неопределенность опыта.

Выражение (5) можно записать в компактной форме:

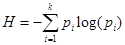(6)

(6)

Если число опытов N, то в силу аддитивности энтропии

(7)

Функция (6) называется средняя энтропия опыта, энтропия выбора, а также информационная энтропия дискретного множества. Энтропия как мера неопределенности (7) была введена Шенноном при разработке математической теории связи. Поскольку понятие энтропия стало общенаучным, то указание на ее информационное происхождение используется лишь в том случае, если по тексту следует различать информационную и термодинамическую (физическую) энтропию.

1.2. Основные свойства энтропии

Рассмотрим основные свойства энтропии дискретного множества. Прежде всего, отметим, что энтропия дискретного множества не может принимать отрицательного значения. Так как 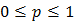, то величина 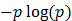всегда положительна.

Если 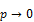, то 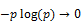, если 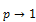, то также .

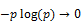Так как 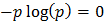только пр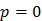и или 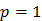, то энтропия опыта равна нулю только в том случае, когда одна из вероятностей равна единице, следовательно, все остальные равны нулю. Это хорошо согласуется со смыслом величины Н как меры неопределенности: в этом случае опыт не содержит никакой неопределенности, так как результат опыта можно предвидеть заранее. Рассмотрим пример: в ящике находятся белые и черные шары одного размера. Вынимаем наугад шар из ящика. Данный опыт имеет два исхода: мы можем вынуть из ящика только белый или черный шар.

Запишем формулу энтропии для двух исходов опыта:

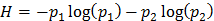
где p ₁ – вероятность извлечения белого шара;
р ₂ - вероятность извлечения черного шара,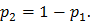

Тогда

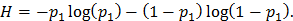
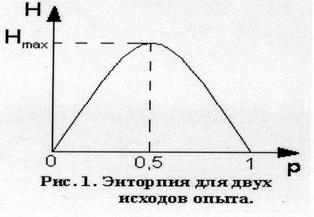
На рис 1. изображен график функции Н для двух исходов опыта. Из которого видно, как изменяется энтропия при изменении вероятности одного из исходов опыта от нуля до единицы. Из графика следует, что максимальное значение энтропии соответствует равновероятным событиям 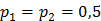. При этом максимальное значение энтропии при выборе двоичного основания логарифма равно единице, т.е.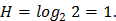

В общем случае для k исходов опыта максимальное значение энтропии соответствует .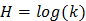

Максимум энтропии отвечает равновероятным событиям, и это хорошо согласуется со смыслом энтропии. В случае равновероятных событий нельзя отдать предпочтение ни одному из них и, таким образом, результат предвидеть труднее всего. Понятие энтропии очень тесно связано с понятием количества информации.

Единица измерения энтропии

Если опыт имеет только два исхода, которые характеризуются равными вероятностями р = 0.5, то выражение (6) при использовании двоичного логарифма примет вид:

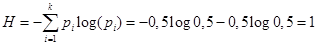(8)

Следовательно, единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями. Эта единица получила название 1 бит. Например, в опыте с бросанием монеты (орел, решка) неопределенность опыта А равна 1 бит, в ячейке компьютера 1 бит информации. Наряду с битом получила распространение более укрупненная единица - байт (1 байт = 8 бит).

1.3. Энтропия как мера разнообразия,

неупорядоченности, хаоса

До сих пор понятие энтропии мы связывали с неопределенностью. Энтропия допускает и другое толкование.

Представим себе систему, состоящую из камеры, в которой находятся N шаров разного сорта, например, отличающихся цветом. Предполагаем, что N достаточно большое число. Обозначим долю шаров i-го сорта (цвета) – x 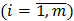. Проведем следующий опыт: наугад извлечем шар из камеры. Вероятность извлечения шара i-го сорта равна .

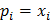При этом следует принять, что размеры шаров одинаковы, в противном случае вероятность извлечения шаров i-го сорта не будет точно соответствовать их доле в камере.

Энтропия всех опытов над системой равна:

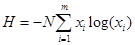(9)

Правая часть выражений (8) и (9) включает параметры рассматриваемой системы. Возникает вопрос, с какой точки зрения эти функции характеризуют содержимое камеры. Первая из функций (8) характеризует степень неупорядоченности системы или степень разнообразия в ней с точки зрения выбранного признака для различения элементов системы (цвета шаров). Если бы в камере находились шары одного сорта, тогда одно из значений р равнялось бы единице, а все остальные нулю, и энтропия приняла бы нулевое значение. Это означает, что система полностью упорядочена или, что то же самое - в системе отсутствует разнообразие по оцениваемому признаку (в данном случае - цвету). Вторая функция (9) измеряет неупорядоченность (разнообразие) в системе несколько иначе. Отличие этих двух функций можно иллюстрировать следующим примером. Если камеру разделить на две части, то при достаточно большом количестве шаров в ней доля шаров i -го сорта в каждой их двух частей останется прежней, но число шаров уменьшится вдвое, вдвое уменьшится неупорядоченность, оцениваемая формулой (9). Однако степень неупорядоченности для каждой из двух частей останется прежней, равной степени неупорядоченности системы. Таким образом, функция (8) не зависит от количества элементов в системе. Такие характеристики в термодинамике называют интенсивными. Напротив, функция (9) зависит от числа элементов. Такие характеристики в термодинамике носят название экстенсивных. Неупорядоченность системы часто отождествляют с уровнем хаоса и неоднородности в ней. По аналогии с выше рассмотренным примером можно оценить неупорядоченность потока смеси каких-либо веществ:

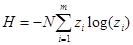, (10)

где z₁ – концентрация i -го компонента в мольных долях ;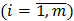
N – расход потока иди число молекул, проходящее через некоторое сечение в единицу времени;
m – количество компонентов в смеси.

Таким образом, видно, что энтропия оценивает разнообразие элементов в системе по некоторому определенному признаку, который может нас интересовать в той или иной задаче.

1.4. Энтропия как мера количества информации

В основе всей теории информации лежит открытие, что информация допускает количественную оценку. В простейшей форме эта идея была выдвинута еще в 1928 году Хартли, но завершенный и общий вид придал ей Шеннон (7) в 1948 году.

Процесс получения информации можно интерпретировать как изменение неопределенности в результате опыта или сообщения.

Вернемся к простейшим опытам с монетой или костью. Перед проведением опыта существует некоторая неопределенность, связанная с незнанием результата опыта. После проведения опыта, т.е. после получения результата, эта неопределенность устраняется. В практике чаще всего встречаются случаи, когда после проведения опыта еще остается некоторая неопределенность.

Если неопределенность до опыта составляла Н, а после опыта H₁, то устраненная в ходе опыта неопределенность составляет:

(11)

Разность априорной (до опыта) энтропии Н и апостериорной (после опыта) энтропии H₁, носит название количества информации.

Таким образом, количество информации замеряется количеством снятой неопределенности. В частном случае, когда неопределенность в результате опыта снимается полностью, т.е. H₁ = 0, получаем I = Н. Хотя количество информации численно равно энтропии, следует иметь ввиду различный смысл количества информации и энтропии.

Количество информации, как и энтропия измеряется в битах. Один бит информации - это количество информации, сообщающее о том, какое из двух равновероятных событий имело место, т.е. такое количество информации, которое уменьшает вдвое число возможных исходов (см. п. 1.3).Ранее мы познакомились с энтропией как мерой неопределенности и неупорядоченности (разнообразия). Из вышесказанного следует, что энтропию можно считать также как меру количества информации.

Рассмотрим пример нахождения количества информации (11) (пример из области математики). Необходимо найти корень уравнения, используя численный метод решения.

Пусть известно, что корень уравнения находится на отрезке от 0 до 100 и отыскивается с точностью до 1. Корень уравнения найдем перебором всех возможных вариантов, их число k = 100. Вероятность отыскания корня на единичном отрезке равна р = 1/k = 0.01, поскольку все отрезки равновероятны.

Неопределенность до опыта (априорная энтропия), т.е. до решения уравнения равна:

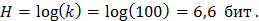
Пусть мы перебрали значения от 0 до 95 (k = 95), но корень не нашли. Осталось перебрать еще 5 вариантов (k = 5). Тогда остаточная (апостериорная) неопределенность после опыта составит:

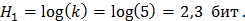
Количество информации равно устраненной неопределенности

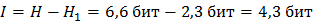
Если мы перебрали все значения от 0 до 100 и нашли корень уравнения, тогда неопределенность после опыта H ₁ = 0 и количество информации I=H.

Из приведенного примера видно, что количество информации не связано с ценностью информации. В современной физике количество информации – понятие объективное, а не субъективное.

1.5. Энтропия непрерывного множества

На практике мы сталкиваемся с ситуацией, когда число исходов опыта может быть сколь угодно велико, т.е. 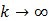. Например, попытаемся оценить неопределенность опыта, связанного со случайным поиском в заданном интервале значения корня из предыдущего примера. Повышая требования к точности ответа можно ожидать сколь угодно большого числа возможных исходов этого опыта. При этом вероятность каждого исхода стремится к нулю (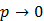), а искомый корень может принимать все возможные значения в заданном интервале (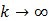). Из теории вероятности известно, что в данном случае необходимо использовать плотность распределения вероятности Р(х).

Эта функция обладает тем свойством, что величина Р(х)dх есть вероятность того, что переменная х (значения корня в рассматриваемом примере) примет значения, заключенные в интервале от х до (х + dх).

Для оценки неопределенности опыта необходимо использовать энтропию непрерывного множества, которое по аналогии с энтропией дискретного множества (6) имеет вид:

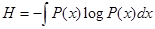(12)

При этом всегда

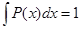
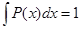
(аналогично случаю дискретного множества 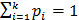). Интегрирование осуществляется в интервале переменной х.

Энтропия непрерывного множества (12) обладает большинством свойств энтропии дискретного множества.

Распределение Р (х), которое соответствует максимальному значению энтропии, имеет вид:

,

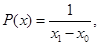
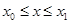где х₀, х₁ – пределы интегрирования.

При этом, если обозначить l = х₁ - х₀, то вероятность обнаружить корень уравнения на отрезке длиной l внутри интервала dx равна р = dx/l

По определению вероятности:

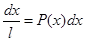
Отсюда

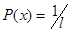(13)

Перепишем формулу (12) с учетом (13)

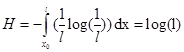
Итак, энтропия непрерывного множества запишется

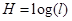(14)

Это выражение аналогично 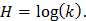для энтропии дискретного множества (4).

Таким образом, если для дискретного множества энтропия измеряет неопределенность (неупорядоченность) абсолютным образом и энтропия дискретного множества всегда положительна, то в случае непрерывного множества под логарифмом формулы (14) может стоять величина меньше единицы и энтропия примет отрицательное значение. Однако, это не имеет принципиального значения, т.к. при анализе систем представляет интерес не сама энтропия, а разность энтропий, то отмеченное свойство энтропии непрерывного множества не вносит каких-либо осложнений в расчеты.

1.6. Количество информации как критерий оценки степени

организованности системы

Как показано выше, энтропия является не только мерой неопределенности (7), но и мерой разнообразия, неупорядоченности, хаоса (9). Тогда вместо определения «устраненная неопределенность» можно употребить термин «блокированное разнообразие».

Термин «устраненная неопределенность» относится к энтропии, записанной через вероятность (7). Это определение ближе к теории информации (см. 1.4):

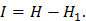
Если энтропия является мерой разнообразия (9), то употребляется термин «блокированное разнообразие». Это определение ближе к физике, термодинамике:

,

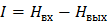(15)

где I – блокированное разнообразие;
Н_вх - энтропия, оценивающая неупорядоченность на входе системы;
Н_вых - энтропия, оценивающая неупорядоченность на выходе системы.

В кибернетике биологом Эшби был сформулирован закон «необходимого разнообразия». Согласно закону Эшби: каждая система, блокирующая разнообразие, должна иметь собственное разнообразие не менее блокированного, т.е. «только разнообразие может уменьшить другое разнообразие».

Этот закон проводит очень простой принцип. Процесс с возрастанием энтропии происходит самопроизвольно. Для осуществления процесса с понижением энтропии требуется некоторая организация процесса, например, наличие специальных установок.

Критерии степени оценки организованности системы в общем виде записывается как отношение

,

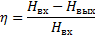(16)

где η – критерий оценки степени организованности системы.

В термодинамической интерпретации этот критерий есть отношение термодинамически минимальной работы разделения исходной смеси на заданные продукты, к аналогичной работе разделения на абсолютно чистые продукты.

Поскольку разность в числителе (16) есть количество информации, то этот критерий можно рассматривать также как информационный

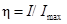
В качестве примера рассмотрим разделение в ректификационной колонне F молей многокомпонентной смеси состава z_i, на дистилят D и кубовый остаток W (рис.2).

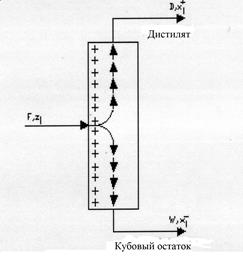
Рис 2. Схема ректификационной колоны

z_i – мольная доля i -го компонента в питании ();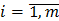
F – расход питания;
D – количество дистилята;
W – количество кубового остатка;
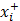– мольная доля i -го компонента в дистиляте ();
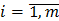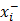– мольная доля /-го компонента в кубовом остатке ();
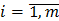ε_y – относительный отбор дистилята;
ε_x – относительный отбор кубового остатка;
m – количество компонентов смеси.

Для процесса ректификации обозначим: HF – энтропия потока питания, НD – энтропия потока дистилята, НW – энтропия кубового остатка.

Блокированное разнообразие (15) запишем в виде:

,

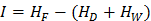где , ,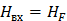

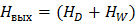Для процесса разделения энтропия потоков может быть рассчитана по формуле (10)

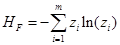
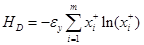(17)

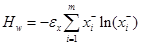
Критерий оценки степени организованности системы (16) для разделительных систем:

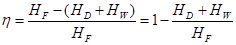(18)

С помощью критерия (18) удобно оценивать разделительную способность колонны: чем больше разность 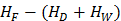, т.е. блокированное разнообразие 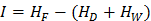, тем выше разделительная способность колонны и, соответственно, тем лучше качество разделения.

Критерий (18) нормирован на единицу. Максимально возможная разделительная способность ректификационной колонны соответствует 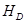=0 и 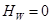, т.е. Н_вых=0. Тогда 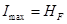F и η=1. Это отвечает гипотетическому случаю, когда колонна делит бинарную смесь (m =2) на чистые продукты или многокомпонентную смесь на две чистые фракции. Практически такой режим недостижим. Критерий 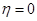, если 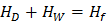, т.е. процесс сводится к простому делению смеси на два потока без изменения исходного состава (отсутствие разделения смеси на компоненты).

С помощью критерия η может оцениваться как разделительная способность колонны, так и многоколонной установки в целом.

С точки зрения характера воздействия на организованность системы варьируемые параметры можно разбить на две группы: интенсивные и экстенсивные.

Интенсивные параметры в состоянии повысить организо­ванность системы (качество разделения) при неизменных затратах работоспособной энергии и фиксированных энергети­ческих затратах. Изменение этих параметров обяза­тельно приво­дит к экстремальному значению критерия качества разделения.

Экстенсивные параметры могут повысить организованность системы только за счет энергетических или неэнергетических затрат.

Доля отбора дистиллята (кубового остатка), место ввода питания являются интенсивными параметрами. Количество орошения, число степеней разделения можно рассматривать как экстенсивные параметры. Таким образом, одну и ту же цель, например, повышение качества разделения, можно достичь либо интенсивным, либо экстенсивным воздействием на систему. Естественно, что в том случае, когда исчерпаны интенсивные пути, при оптимизации следует пользоваться экстенсивным воздействием.

Выражение (18) применяется как критерий оптимальности в задачах оптимизации процессов разделения смеси. При этом, критерий η используется как относительная оценка качества разделения. В общем случае, число входных потоков может быть любым. Естественно добиваться максимального значения η для действующей ректификационной колонны. Если величина Н_F фиксирована, то максимализация η сводится к минимизации энтропии выходных потоков.

Таким образом, в задачах оптимизации с фиксированной энтропией входных потоков реализуется принцип минимальной энтропии. Однако следует обратить внимание, что в задачах описания процессов (раздел 3) будет использован принцип максимальной энтропии (максимального правдоподобия).