Глава 1. Выборочный метод

Пусть требуется изучить некоторую совокупность объектов. Множество всех изучаемых объектов называется генеральной совокупностью. Выборочной совокупностью (или просто выборкой) называется совокупность объектов, отобранных для исследования из генеральной совокупности. Объемом совокупности (генеральной или выборочной) называют число объектов этой совокупности.

Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы объем выборки был достаточно велик, и, кроме того, объекты выборки должны правильно представлять генеральную совокупность (т.е. выборка должна быть репрезентативной).

Выборки подразделяются на повторные (отобранный объект перед отбором следующего возвращается в генеральную совокупность) и бесповторные (отобранный объект не возвращается в генеральную совокупность).

Пусть из генеральной совокупности извлечена выборка объемом n. Упорядоченная выборка, записанная в порядке возрастания, называется вариационным рядом.

Разность между крайними членами вариационного ряда (наибольшим и наименьшим значениями выборки) называется размахом вариационного ряда. Вариационный ряд называется дискретным, если значения признака отличаются друг от друга на некоторую постоянную величину (например, ряд распределения рабочих по тарифному разряду). Вариационный ряд называется непрерывным, если значения признака могут отличаться один от другого на сколь угодно малую величину (например, ряд распределения рабочих по уровню заработной платы).

Наблюдаемые значения х_i называются вариантами. Число повторений наблюдаемых значений называется частотой варианта или весом. Относительной (эмпирической) частотой значения х_i называется отношение 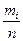, где m_i – число повторения значения х_i в выборке объема n.

Наряду с понятием частоты существует понятие накопленной (накопительной) частоты m_xi, которая показывает, во скольких наблюдениях признак принял значения меньше значения х:

m_x = m_x1 + m_x2 + … + m_xi,

где х₁, х₂, …, х_i < x.

При большом числе наблюдений статистическое распределение выборки можно задать в виде последовательности интервалов, обычно равной длины и соответствующих им частот (в качестве частоты интервалов принимают сумму частот вариант, попавших в этот интервал).

При построении интервального вариационного ряда распределения необходимо определить:

1) число групп к по формуле Серджеса

к=1 + 3,322lgn,

где n – объем выборки;

2) длину интервала

h =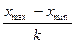

3) за начало первого интервала рекомендуется брать величину

x_нач = х_min – 0,5h

Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов (полигоном, гистограммой и кумулятой).

Полигоном частот называют ломанную, отрезки которой соединяют точки (x_i; m_i), где x_i – варианты выборки, m_i - соответствующие им частоты или точки (x_i; 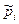), где 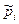- относительные частоты.

Кумулята – графическое изображение накопленных частот. Кумулята строится по точкам (x_i; m_xi). Для интервального ряда распределения в качестве x_i принимают середины интервалов.

Гистограмма строится только для интервального вариационного ряда. На каждом из интервалов значений как на основании, строят прямоугольник с высотой, пропорциональной частоте m_i.

Для оценки интегральной функции распределения генеральной совокупности служит эмпирическая функция распределения. Эмпирической функцией распределения называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х<х, то есть относительную накопленную частоту

F*(x) = ,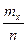

где m_x – число вариант, меньших х,

n – объем выборки.

Эмпирическая функция распределения F*(x) обладает всеми свойствами интегральной функции распределения F(x):

1) F*(x) 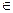[0; 1];

2) F*(x) – неубывающая функция;

3) если х₁ – наименьшая варианта, а х_к – наибольшая, то F*(x)=0 при х ≤х₁ и F*(x)=1 при х >х_к.