 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ранг матрицы
|
|
Справочный материал.
Пусть дана матрица, содержащая m строк и n столбцов. Выделим в ней произвольным образом к строк и к столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют матрицу к -ого порядка, определитель которой называется минором к -ого порядка матрицы  .
.
Рангом матрицы  называется максимальное число линейно независимых столбцов этой матрицы. Обозначение:
называется максимальное число линейно независимых столбцов этой матрицы. Обозначение: 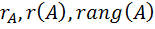 .
.
В курсе высшей алгебры доказывается, что ранг матрицы равен наибольшему порядку миноров этой матрицы, отличных от нуля.
Свойства ранга матрицы.
1. Если матрица  имеет размер
имеет размер 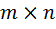 , то:
, то:
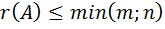 .
.
2. 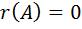 тогда и только тогда, когда все элементы матрицы
тогда и только тогда, когда все элементы матрицы  равны нулю.
равны нулю.
3. Если  – квадратная матрица порядка n, то
– квадратная матрица порядка n, то 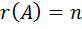 тогда и только тогда, когда
тогда и только тогда, когда 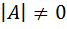 .
.
С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
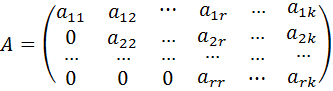 ,
,
где 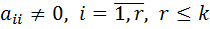 .
.
Теорема. При элементарных преобразованиях ранг матрицы не меняется.
Ранг ступенчатой матрицы равен r, то есть количеству ненулевых строк.
Ранг матрицы можно найти двумя способами.
Первый способ (с помощью окаймляющих миноров). Сначала нужно найти отличный от нуля минор первого порядка. Если такого нет, то ранг матрицы равен 0. Затем найти отличный от нуля минор второго порядка, содержащий найденный выше отличный от нуля минор первого порядка. Если такого нет, то ранг матрицы равен 1. Далее найти отличный от нуля минор третьего порядка, содержащий найденный выше отличный от нуля минор второго порядка. Если такого нет, то ранг матрицы равен 2 и т. д.
Второй способ (с помощью элементарных преобразований). С помощью элементарных преобразований матрицу привести к ступенчатому виду. Количество ненулевых строк полученной матрицы равно рангу матрицы.
Элементарные преобразования матрицы.
1. Отбрасывание нулевой строки (столбца) матрицы.
2. Умножение всех элементов строки (столбца) матрицы на число, не равное 0.
3. Изменение порядка строк (столбцов) матрицы.
4. Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца).
5. Транспонирование матрицы.
Пример. Найти ранг матрицы
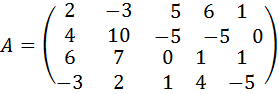 .
.
Решение.
Первый способ. Найдём отличный от нуля минор первого порядка. Например, можно взять 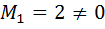 . Затем найдём отличный от нуля минор второго порядка, содержащий минор
. Затем найдём отличный от нуля минор второго порядка, содержащий минор 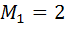 . Например,
. Например, 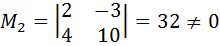 . Далее найдём отличный от нуля минор третьего порядка, содержащий минор
. Далее найдём отличный от нуля минор третьего порядка, содержащий минор 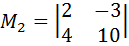 . Например:
. Например:
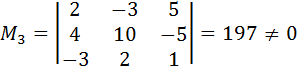 .
.
Далее найдём отличный от нуля минор четвёртого порядка, содержащий минор 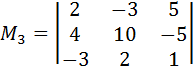 . В этом примере существуют два минора четвёртого порядка, содержащие
. В этом примере существуют два минора четвёртого порядка, содержащие 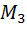 :
:
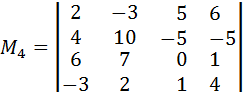 и
и 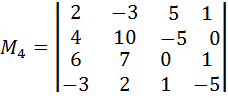 .
.
Можно показать, что оба минора равны 0. Следовательно, ранг матрицы  равен 3.
равен 3.
Второй способ. Приведём матрицу к ступенчатому виду с помощью следующих элементарных преобразований.
1) Ко второй строке прибавим первую, умноженную на (–2), к третьей строке прибавим первую, умноженную на (–3):
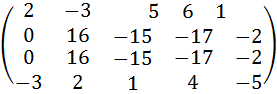 .
.
2) К третьей строке прибавим вторую, умноженную на (–1):
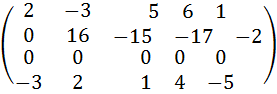 .
.
3) Вычеркнем нулевую строку:
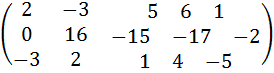 .
.
4) Первую строку умножим на 3, третью строку умножим на 2:
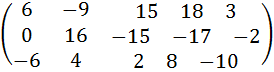 .
.
5) К третьей строке прибавим первую:
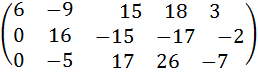 .
.
6) Разделим первую строку на 3:
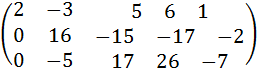 .
.
7) Ко второй строке прибавим третью, умноженную на 3:
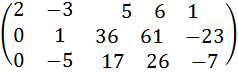 .
.
8) К третьей строке прибавим вторую, умноженную на 5:
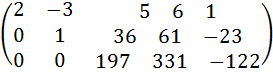 .
.
Матрица приведена к ступенчатому виду. Количество строк полученной матрицы равно 3 и, поэтому, ранг матрицы равен 3.
Ответ: 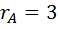 .
.
Задание 15. Найти ранг матрицы.
1. 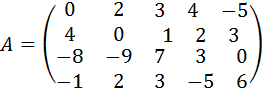 .
.
2. 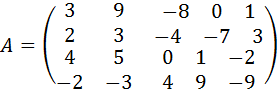 .
.
3. 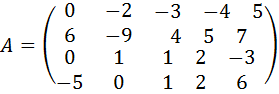 .
.
4. 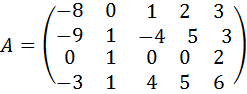 .
.
5. 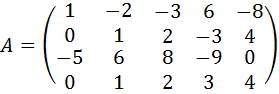 .
.
6. 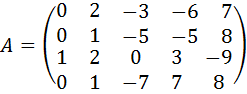 .
.
7. 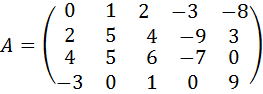 .
.
8. 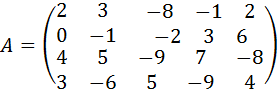 .
.
9. 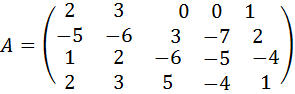 .
.
10. 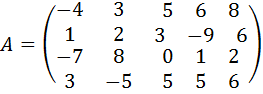 .
.
11. 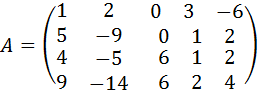 .
.
12. 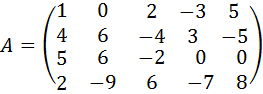 .
.
13. 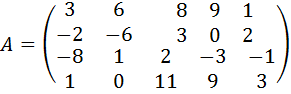
14 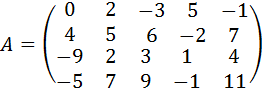 .
.
15. 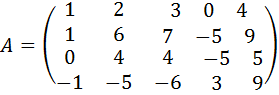 .
.
16. 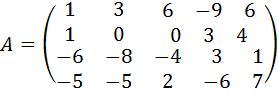 .
.
17. 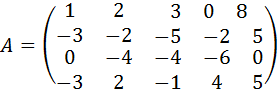 .
.
18. 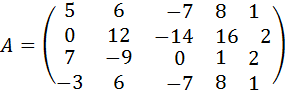 .
.
19. 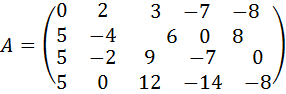 .
.
20. 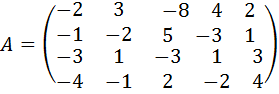 .
.
21. 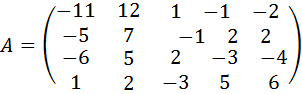 .
.
22. 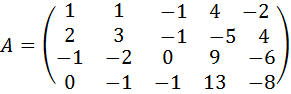 .
.
23. 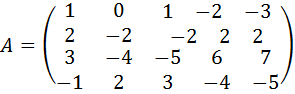 .
.
24. 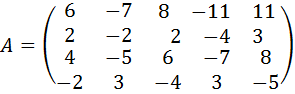 .
.
25. 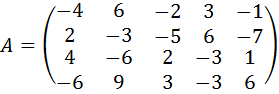 .
.
26. 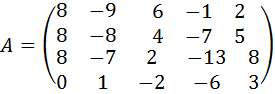 .
.
27. 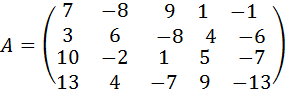 .
.
28. 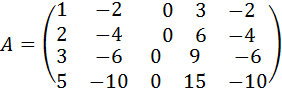 .
.
29. 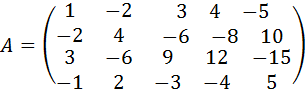 .
.
30. 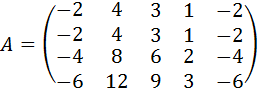 .
.
31. 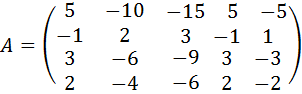 .
.
32. 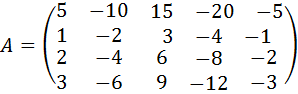 .
.
33. 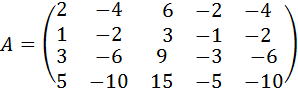 .
.
34. 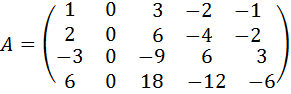 .
.
35. 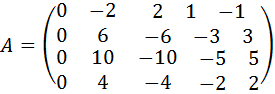 .
.
36. 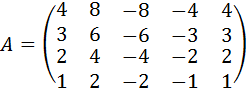 .
.
Дата публикования: 2015-10-09; Прочитано: 936 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
