Примеры. 39.Вероятность нормального расхода электроэнергии в некотором районе города равна 0,6

39. Вероятность нормального расхода электроэнергии в некотором районе города равна 0,6.

а) Составить закон распределения случайной величины Х – числа дней нормального расхода электроэнергии в ближайшие 4 дня;

б) найти интегральную функцию распределения случайной величины Х и построить ее график;

в) найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х.

Решение. а) Число дней расхода электроэнергии Х – это дискретная случайная величина. Ее возможные значения по условию 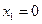, , 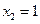, , 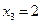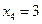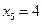. Вероятность каждого возможного значения найдем по формуле Бернулли:

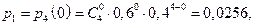
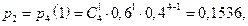
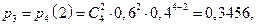
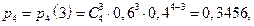
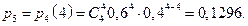
Теперь составим ряд распределения

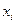
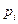
	0,0256	0,1536	0,3456	0,3456	0,1296

и построим многоугольник распределения

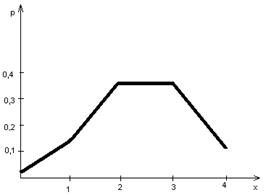
б) Рассмотрим интервал 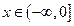. Событие 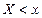для этого интервала является невозможным, так как нет ни одного отрицательного значения Х. Следовательно, 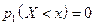. На следующем интервале 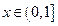для 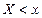имеем 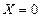. Вероятность этого события равна 0,0256; 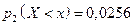. На интервале 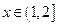Х может принимать значения 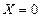и 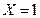. Следовательно, .

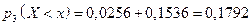Аналогично, ;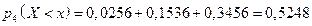

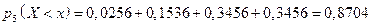и

.

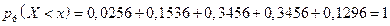Таким образом, интегральная функция распределения 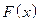имеет вид:

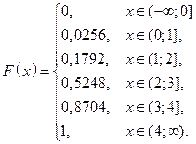
Построим график этой функции

в) Математическое ожидание числа дней нормального расхода электроэнергии найдем по формуле 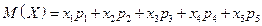, т.е.

.

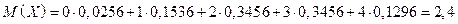Дисперсию вычисляем по формуле :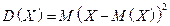

.

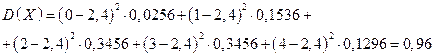Среднее квадратичное отклонение:

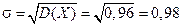
40. Вини Пуху захотелось полакомиться мёдом. Если он заберётся на дерево, то вероятность укуса пчелой равна 0,4.

Составить закон распределения случайной величины Х, если наш герой забирается на 5 деревьев.

Решение. Случайная величина Х – количество укусов пчелой. Случайная величина Х имеет биноминальное распределение.

;

;

;

;

;

;

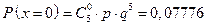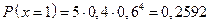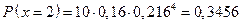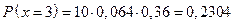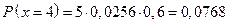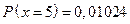х
р	0,07776	0,2592	0,3456	0,2304	0,0768	0,01024

41. Идёт охота на дикого зверя с помощью ловушки. Вероятность попасть в ловушку для волка – 0,3, для медведя – 0,5, для лисы и зайца – 0,6.

Найти закон распределения нормальной величины X – числа попавших в ловушку зверей.

Решение. ; ; ; ; ; ;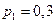

;

; .

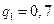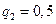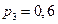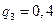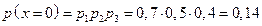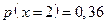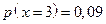х
p	0,14	0,41	0,36	0,09

42. В книге кулинарных рецептов имеется 6 рецептов приготовления первого блюда, 4 – второго блюда. Пять раз подряд выписывают наудачу взятые рецепты. Случайная величина X – число рецептов первых блюд.

Составить закон распределения величины X, найти математическое ожидание и дисперсию.

Решение.

, , .

, , , , , .

, .

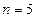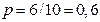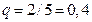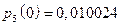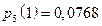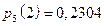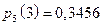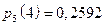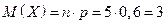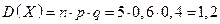x
р	0,01024	0,0768	0,2304	0,3456	0,2592	0,07776

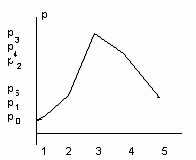
43. Идёт игра в дартс. Вероятность попадания в центр для участника A – 0,8, B – 0,7. Всего пять попыток.

Составить законы распределения числа попаданий для обоих игроков, если первым кидает игрок A, а также закон распределения общего числа попаданий.

Решение.

Число попаданий участника
Вероятность участника A	0,008	0,096	0,384	0,512
Вероятность участника B	0,09	0,42	0,49	--------

Общее число попаданий
Вероятность	0,00072	0,012	0,0788	0,2544	0,4032	0,25088

44. Предлагаются следующие правила игры: если играющий достанет из полного набора домино фишку, сумма очков на которой равна 3, 6 или 9, то получит приз в размере 9, 6 или 3 у.е., соответственно. В противном случае он отдает 2 у.е. Стоит ли соглашаться на игру?

Решение. Фишку с суммой равной 3 можно достать двумя способами: (0+3), (1+2); 6 – четырьмя способами (0+6), (1+5), (2+4), (3+3); 9 – двумя способами (3+6),(4+5).

М (X) = 9*2/28+6*4/28+3*2/28–2*20/28 = 8/28 = 2/7, т.к. математическое ожидание больше нуля, то можно сделать вывод о том, что играть стоит.

45. Сколько раз в среднем нужно бросать игральную кость до появления 6.

Решение. Пусть р – вероятность появления 6, вероятность первого успеха отсюда равна 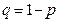. Чем больше количество испытаний, тем больше искомая вероятность.

Количество испытаний				………	n
Вероятность	p	pq	pq 2	……	p × qn –1

Суммарная вероятность равна p + pq + pq ² + pq ³ +….+ pq^{n –1} = p (1+ q + q ²+…+ + q^{n –1});

(1+ q + q ²+…+ q^{n –1}) = 1/(1– q).

Т.о., р /1– q = p /1–1+ P = 1; среднее число испытаний m до первого успеха по определению равно (М (х)):

(1) m = pq +2 pq +3 pq ²+…+ npq^{n –1}.

Для нахождения суммы такого ряда применим способ суммирования геометрических рядов:

(2) qm = pq +2 pq ² +3 pq ³+…+ npq^{n –1} q;

Вычитая (2) из (1) получим:

m – qm = p + pq + pq ²+…+ pq^{n –1};

m (1– q)=1; при этом 1– q =1, следовательно, mp =1, откуда m =1/ p =1/6.

Возможно другое решение задачи:

Если первое испытание неудачно, то условное среднее число испытаний равно 1+ m, а если первое испытание удачно, то условное среднее число испытаний равно 1, т.о. n = p *1+ q (1+ m)=1+ qm, откуда m =1/ p =1/6.

46. Человеку предлагают сыграть в игру, заключающуюся в том, что из колоды в 36 карт достают две карты по одной и возвращают обратно. Выигрыш, номиналом в 4$ происходит тогда, когда появляется хотя бы один козырь. За игру человек платит 2$. Выгодно ли это?

Решение. 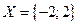, и событие A – появление козыря.

; .

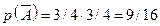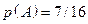Тогда, .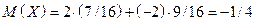

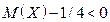, следовательно, играть не выгодно.

47. Выигрыш происходит в том случае, если из полного набора домино достают фишку, сумма очков которой равна 3, 6 или 9, и равен 3, 6 или 9 соответственно. Проигрыш равен 2. Выгодно ли играть и какова плата за участие, чтобы оно было безобидным.

Решение. 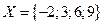; три очка можно получить как 0+3 или 1+2

шесть как 0+6,1+5,2+4 или 3+3,

девять очков как 3+6 или 4+5.

Остальные 20 случаев проигрышные.

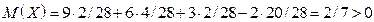– значит это выгодно.

Допустим, что a – безобидное участие в игре. .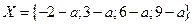

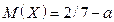, откуда . Т.о. а безобидно при .

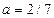48. Абитуриент сдает 2 вступительных экзамена по математике и физике.

Составить закон распределения случайной величины Х, числа полученных пятерок, если вероятность получения пятерки по математике равна 0,8, а по физике – 0,6.

Решение. Возможные значения Х есть 0, 1, 2.

Причем,

; ;

.

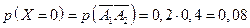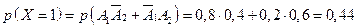x
р	0,08	0,44	0,48

49. Согласно американским статистическим таблицам смертности, вероятность того, что 25-летний человек проживет еще один год, равна 0,992 (следовательно, вероятность того, что он умрет, равна 0,008). Страховая компания предлагает такому человеку застраховать свою жизнь на год на сумму 1000$; страховой взнос равен 10$.

Найти математическое ожидание прибыли компании.

Решение. Величина прибыли Х есть случайная величина со значениями +10$ и –990$. Составим таблицу распределения вероятностей:

х	+10	–990
р	–0,992	0,008

.

Ожидаемая средняя прибыль положительна, что дает возможность страховой компании продолжить дело, оставляя резервный капитал для выплаты страховых сумм, производить административные расходы, получать прибыль.

50. Игра в рулетку. На колесе рулетки имеется 38 одинаково расположенных разметок: 00, 0, 1, 2, …, 36. Игрок может поставить 1$ на любой номер. Если его номер выиграл, игрок получает 36$ (35$ выигрыша плюс 1$ ставки).

Найти математическое ожидание выигрыша.

Решение. Составим таблицу распределения вероятностей:

х	–1	+35
р	37/38	1/38

.

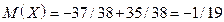Игра не является «справедливой», игорный дом должен обеспечивать себе средний доход на «накладные расходы» и риск.

51. Найт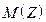и и 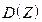для случайной величины Z, если 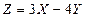и , , , .

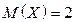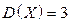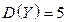Решение. .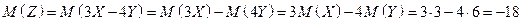

.

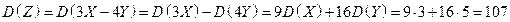52. Вероятность появления события A при каждом из бесконечной последовательности испытаний равна р. Случайная величина x - номер испытания, при котором произошло первый раз событие А. Найти закон распределения случайной величины х.

Решение. Случайная величина x может принимать любое целое положительное значение 1, 2, 3,... Вероятность p₁ того, что событие A произойдет при первом испытании, будет

р₁ = Р(А) = р.

Вероятность р₂ того, что событие не произойдет при первом испытании, а произойдет при втором, будет

р₂ =Р(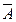 и А) = (1-p)р.

Вероятность р₃ того, что событие A не произойдет ни при первом, ни при втором испытании, а произойдет при третьем, будет

р₃ = Р(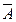 и 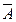и А) = (1-p)(1-p)p = (1-p)²p

и т.д.

p_k = (1-p)^k-1p. (2)

Таблица распределения вероятностей будет

x				…	…	k	…
pk	p	(1-р)р	(1-р)2р	…	…	(l-p)k-lp	…

Здесь также имеем:

53. Вероятность попадания при каждом выстреле p = 0,8. Имеется три снаряда. Определить вероятность того, что будет израсходован один снаряд, два снаряда, три снаряда, если стрельба ведется до первого попадания или промаха всеми тремя снарядами; составить таблицу распределения случайной величины x - числа израсходованных снарядов.

Решение. Пусть x - случайная величина, число израсходованных снарядов; Р(x = x ₁) - вероятность того, что будет израсходовано x ₁ снарядов.

Тогда Р(x = 1) = p = 0,8 равна вероятности попадания при одном (первом) выстреле.

Р(x = 2) = (1-p)p = (1-0,8)×0,8 = 0,16 - вероятность того, что при первом выстреле был промах, при втором выстреле - попадание.

Р(x = 3) = (1-p)² = (1-0,8)×(1-0,8) = 0,2×0,2 = 0,04,

так как всего три снаряда и стрельбу прекращают независимо от того, будет ли при третьем выстреле попадание или промах. Последнюю вероятность можно было вычислить и как разность

1 – Р(x = 1) -Р(x = 2) = 1-0,8-0,16 = 0,04. Таблица распределения будет иметь вид

x
P(x = xk)	0,8	0,16	0,04

54. Изобразить графически биномиальный закон распределения случайной величины x при n = 8, p = 1/2, q = 1/2.

Решение. Определим все значения вероятностей, входящие в таблицу:

Построим многоугольник распределения (рис. 3).

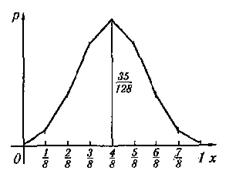
Рис. 3.

55. Какова вероятность того, что событие A произойдет два раза:

а) при 2-х испытаниях;

б) при 3-х испытаниях;

в) при 10 испытаниях,

если вероятность появления события при каждом испытании равняется 0,4?

Решение. а) Здесь n = 2, p = 0,4, q = 0,6:

P ;

б) здесь n = 3, p = 0,4, q = 0,6:

P ;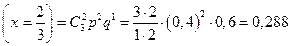

в) здесь n = 10, p = 0,4, q = 0,6:

P .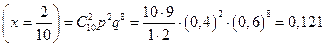

56. По цели производится 5 независимых выстрелов. Вероятность попадания при каждом выстреле равна 0,2. Для поражения цели достаточно трех попаданий. Определить вероятность поражения цели.

Решение. Здесь n = 5, p = 0,2, q = 0, 8. Очевидно, что вероятность поражения следует вычислять по формуле

p_пор = 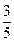Р(x = ) + Р(x = ) + Р(x = )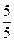

или по формуле

p_пор = 1 - [Р(x = 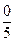) + Р(x = 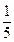) + Р(x = )].

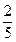По первой формуле имеем

p_пор = + + =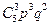

= .

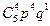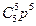57. Производится четыре независимых испытания. Вероятность появления события A при каждом испытании 0,5. Определить вероятность того, что событие A появится не менее двух раз.

Решение. Здесь n = 4, p = 0,5, q = 0,5:

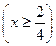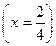P = P 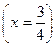+ P + P ,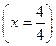

или

P 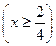= 1 - .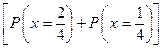

Вычислим вероятность

.

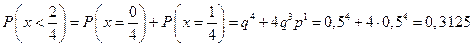Следовательно, по второй из формул получаем

P 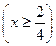= 1 – [(0,5)⁴ - 4×(0,5)⁴] = 0,6875» 0,69.

58. Вероятность брака в данной партии деталей р = 0,1. Какова вероятность того, что в партии из 3-х деталей будет m = 0, 1, 2, 3 бракованных деталей?

Решение.

P 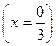= = 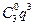1×(0,9)³ = 0,729,

P 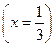= = 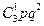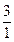×0,1×(0,9)² = 0,243,

P 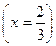= = 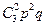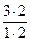×(0,1)²×0,9 = 0,027,

P 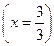= = 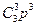0,001.

59. Вероятность попадания при одном выстреле p = 0,2. Определить расход снарядов, обеспечивающих математическое ожидание числа попаданий, равное 5:

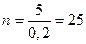снарядов.

60. Производится один выстрел по объекту. Вероятность попадания р. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение. Строим таблицу значений числа попаданий

х
рk	р	q

где q = 1 - р. Следовательно,

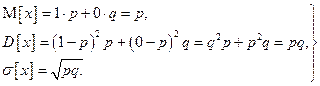. (5)

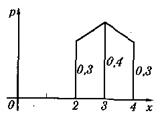
61. Случайная величина x задана следующим законом распределения (см. таблицу и рис. 6):

х
pk	0,3	0,4	0,3

Определить: 1) математическое ожидание, 2) дисперсию, 3) среднее квадратическое отклонение.

Решение.

1. М[ х ] = 2×0,3 + 3×0,4 + 4×0,3 = 3,

2. D[ x ] = (2-3)²×0,3 + (3-3)²×0,4 + (4-3)²×0,3 = 0,6,

3. [ х ] = 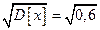= 0,77.

Рис. 6.	Рис. 7.	Рис. 8.

62. Случайная величина x задана следующим законом распределения (см. таблицу и рис. 7):

x
pk	0,3	0,4	0,3

Определить: 1) математическое ожидание, 2) дисперсию, 3) среднее квадратическое отклонение.

Решение.

1. М[ х ] = 1×0,3 + 3×0,4 + 5×0,3 = 3,

2. D[ x ] = (1-3)²×0,3 + (3-3)²×0,4 + (5-3)²×0,3 = 2,4,

3. [ х ] = 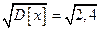= 1,55.

Рассеивание, разброс случайной величины в первом примере меньше рассеивания случайной величины во втором примере (см. рис. 7 и 8). Дисперсии этих величин соответственно равны 0,6 и2,4.

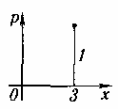
63. Случайная величина х задана следующим законом распределения (см. таблицу и рис. 8):

х
р

Определить: 1) математическое ожидание, 2) дисперсию, 3) среднее квадратическое отклонение.

Решение.

1. М[ х ] = 3×1 = 3,

2. D[ x ] = (3-3)²×1 = 0,

3. [ х ] = 0.