Несобственные интегралы. òf(x) dx = lim òf(x) dx

Несобственные интегралы второго рода это интегралы на конечном отрезке от функций, котрые терпят бесконечный разрыв.

Если функция f(x) имеет бесконечный разрыв в точке с отрезка [ a,b ] и непрерывна при a £ x < c и c< x£ b, то по определению полагают

_{b c-a b}

òf(x) dx = lim òf(x) dx + lim òf(x) dx

^{a a®0 a b®0 c+b}

Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры.

_+¥

1. Вычислить ò 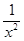dx

¹ _{+¥ b b}

По определению ò 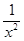dx = lim ò 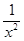dx = lim (- 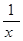) = lim (- 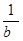+1)=1,

^{1 b® +¥ 1 b® +¥ 1 b® +¥}

т.е. искомый несобственный интеграл равен 1.

Используя формулу Ньютона-Лейбница, можно убедиться, что

_+¥

ò 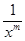dx

¹

является сходящимся к 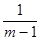если m>1 и расходящимся, если m£1.

Геометрический смысл этого результата состоит в том, что среди всех кривых вида y= 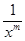гипербола y= 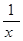является своеобразным “порогом”.

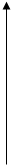
y

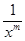y= (m<1)

1 y=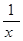

1 x

_+¥

2. Вычислить (или установить расходимость) òcosx dx

⁰

По определению имеем

_{+¥ b b}

òcosx dx = lim òcosx dx = lim (sinx½)= lim (sinb-sin0)=lim sinb,

^{0 b® +¥ 0 b®+¥ 0 b®+¥ b®+¥}

Последний предел не существует. Следовательно, несобственный интеграл расходится.

_+¥

3. Найти ò 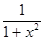dx

^-¥ _{+¥ +¥}

Подынтегральная функция четная, поэтому ò 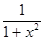dx =2ò 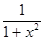dx

_{+¥ b} ^-¥ _b ⁰

Тогда ò 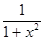dx= lim ò1/(1+x²) dx= lim arctg x½ = lim arctg b=p/2

⁰ _+¥ ^{b®+¥ 0 b®+¥ 0 b®+¥}

Т.о., ò 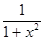dx=p сходится.

^-¥

_+¥

4. Найти ò xe^-x2 dx.

_+¥ ⁰ _{b b}

Имеем ò xe^-x2 dx=lim[- 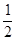òe^-x2 d(-x²)]=lim[ 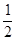e^-x2½]= lim[- 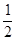e^-b2+ ]= ,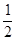

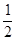^{0 b®+¥ 0 0 b®+¥}

₁

5. Найти ò1/x dx.

⁰

Подынтегральная функция f(x)=1/x в точке x=0 неограничена. Поэтому:

_{1 1 1}

ò 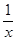dx= lim ò 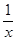dx= lim(lnx½)=lim(ln(1)-ln(a))=+¥

^{0 a®0 a a®0 a}

Несобственный интеграл расходится.