Нормальное распределение. Его обозначают N(а, ); саму случайную величину также называют нормальной

Случайная величина имеет нормальное (гауссовское) распределение с параметрами а и 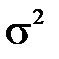, если ее плотность распределения задается формулой:

.

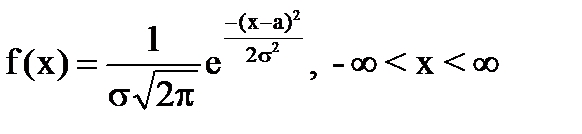Его обозначают N(а, 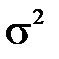); саму случайную величину также называют нормальной. На практике распределение случайных величин чаще всего приближается именно к этому закону распределения.

График плотности нормального распределения (его еще называют нормальной, или гауссовской кривой) представлен на рисунке 14.

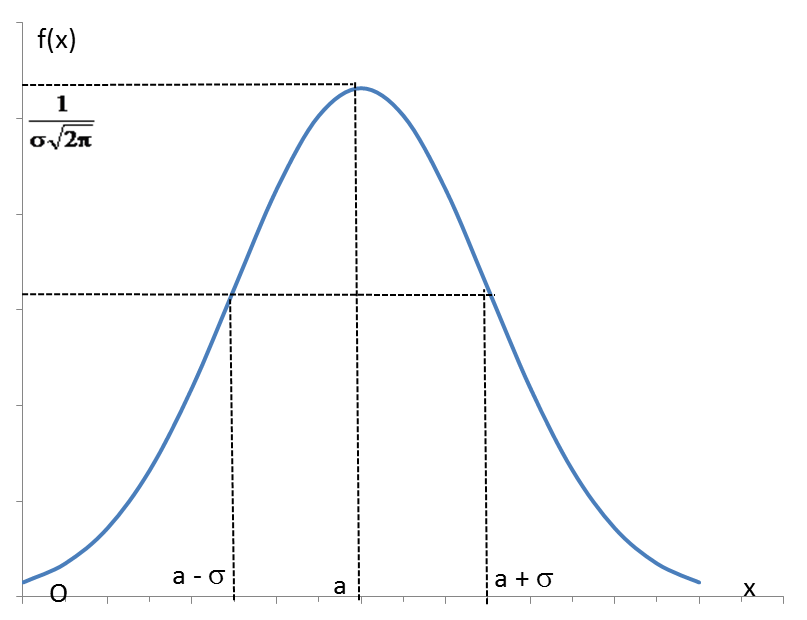
Рисунок 14 – Нормальная кривая

Как видно из рисунка 14, нормальное распределение является симметричным относительно прямой x = а. Можно доказать, что параметр а представляет собой математическое ожидание случайной величины (центр распределения). Поскольку параметр а определяет положение графика плотности на числовой оси, его еще называют параметром положения. В точке x = а плотность распределения достигает максимума, который равен .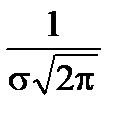

Дисперсия нормального распределения равна 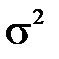. Параметр 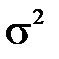характеризует степень сжатия или растяжения графика плотности, поэтому его называют параметром масштаба.

Ось абсцисс является горизонтальной асимптотой нормальной кривой, т.е. .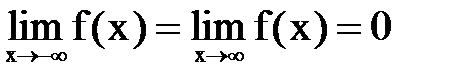

Также этот график имеет две точки перегиба 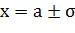, ординаты которых равны .

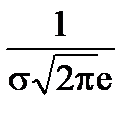График функции нормального распределения приведен на рисунке 15. Этот график центрально симметричен относительно своей точки перегиба, имеющей координаты (а; 0,5). Он имеет две горизонтальные асимптоты – ось абсцисс и параллельную ей прямую с ординатой, равной единице.

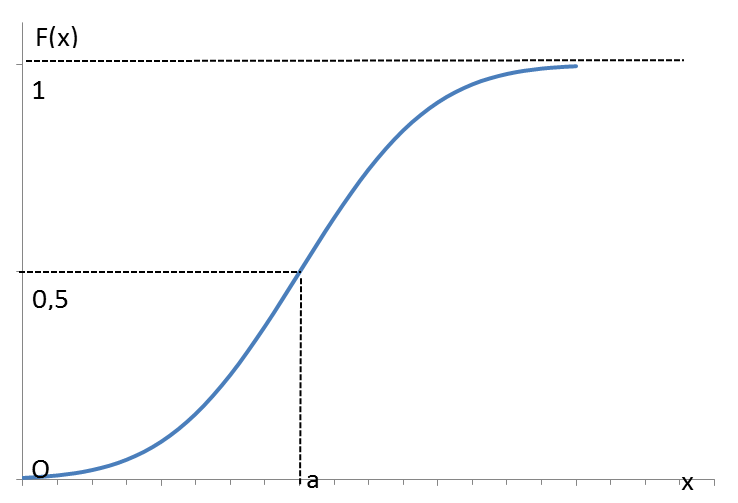
Рисунок 15 – Функция нормального распределения

Непосредственно найти функцию нормального распределения представляется затруднительным, поскольку интеграл от плотности нормального распределения является «неберущимся» в элементарных функциях. Поэтому для проведения расчетов используют частный случай нормального распределения – стандартное нормальное распределение, которое будет рассмотрено далее.

Нормальное распределение используется при моделировании разнообразных ситуаций, связанных с измерениями веса и объема товаров, срока работы электроламп, роста мужчин, проходящих медкомиссию и т.п. Во всех этих случаях случайная величина – результат измерения – распределена симметрично относительно своего среднего случайного значения.

Ясно, что на практике эти величины обычно принимают значения из некоторого интервала, а не на всей числовой оси. Тем не менее, это не препятствует использованию нормального распределения. При исследовании случайных величин, который подчиняются нормальному закону, используют “правило трех сигм”, согласно которому отклонение нормальной случайной величины от своего математического ожидания более чем на 3 практически невозможно (его вероятность ничтожно мала). Это позволяет ограничиться рассмотрением интервала [a - 3 ; a + 3 ].

Пусть случайная величина у распределена по N(а, 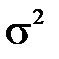). Поставим в соответствие этой случайной величине другую случайную величину х, значения которой вычисляются по формуле х = (у - а)/ . В соответствии с известными свойствами математического ожидания и дисперсии

М(х) = М((у - а)/ ) = М(у - a)/ = (а - а)/ = 0;

D(x) = D((у - а)/ ) = D(у - a)/ ² = ( ² - 0)/ ² = 1.

Величина х будет иметь нормальное распределение с параметрами
а = 0, ² = 1, т.е. N(0, 1). Его называют стандартным (или нормированным) нормальным распределением.

Плотность распределения N(0, 1) определяется формулой:

.

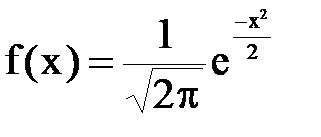Функция распределения N(0, 1) определяется:

.

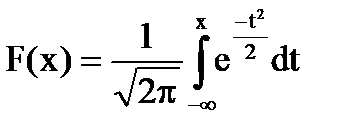Отметим, что для N(0, 1) центром распределения является 0. Поэтому
f(-x) = f(x), а F(-x) = 1 - F(x) (смотри рисунок 16).

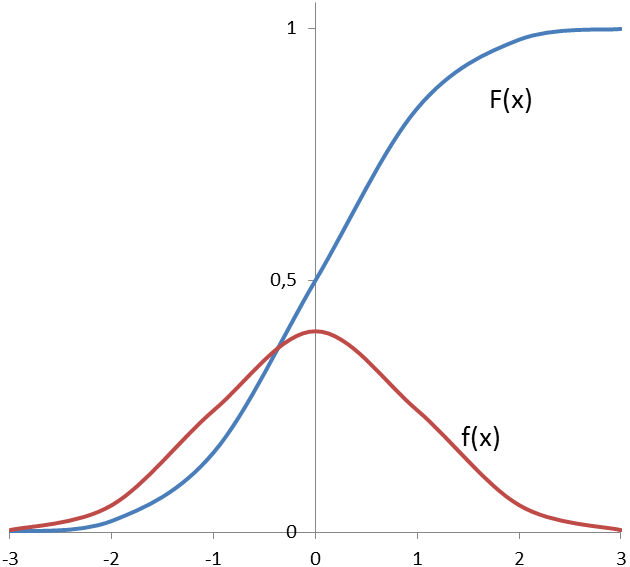
Рисунок 16 – Функция и плотность стандартного нормального распределения

Значения функции стандартного нормального распределения табулированы для неотрицательных х.

При этом обычно табулируется даже не сама функция распределения, а функция 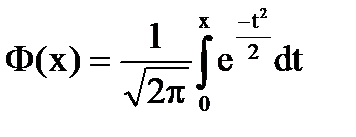, которая называется функцией Лапласа. В этом случае, чтобы получить функцию распределения, необходимо к значению, приведенному в таблице, прибавить ½ (ведь 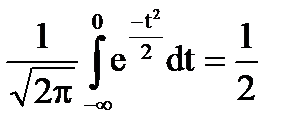, так как 0 – центр распределения). Соответственно для отрицательных х функцию распределения можно найти по формуле F(-x) = 1/2 - Ф(x).

Часто в справочных таблицах приводят удвоенную функцию Лапласа, которую рассчитывают по формуле 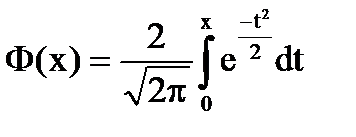. В этом случае ее значения необходимо разделить на 2.

Например, производителю электроламп известно, что средний срок работы лампы составляет 600 часов, а стандартное отклонение срока работы – 40 часов. Определим вероятность того, что лампа проработает:

а) менее 700 часов;

б) менее 550 часов;

в) от 550 до 700 часов.

г) пусть 2% ламп работают не более определенного срока (имеют минимальный срок работы). Определим его величину.

Случайная величина х – срок работы электролампы в часах – распределена нормально с математическим ожиданием 600 и дисперсией 1600.

а) Р (х < 700) = F`(700), где F`(х) – функция распределения N(600, 1600).

Чтобы найти эту вероятность, перейдем к N(0, 1): Р(х < 700) = F((700 - 600)/40) = F(2,5). Эту величину находят по таблице: Р(х < 700) = 0,5 + Ф(2,5) = = 0,5 + 0,4938 = 0,9938.

Следовательно, не более 700 часов работают 99,38% ламп.

б) Р(х < 550) = F`(550) = F((550 - 600)/40) = F(-1,25) = 1 - F(1,25) = ½ - Ф(1,25) = 0,5 - 0,3914= 0,1056.

Следовательно, не более 550 часов работают 10,56% ламп.

в) Р(550 < х < 700) = F`(700) - F`(550) = 0,9938 - 0,1056 = 0,8882.

Следовательно, от 550 до 700 часов работают 88,81 % ламп.

г) Определим вначале, какому значению стандартной нормальной величины х^* соответствует значение функции распределения 0,02. Поскольку речь идет о лампах с самым коротким сроком работы, это значение будет меньше среднего, а значит, при переходе к стандартному нормальному распределению будет получено отрицательное значение (меньшее 0). Тот же вывод можно было сделать на основании того, что 0,02 < 0,5 (функция распределения монотонно возрастает, и равна 0,5 в точке 0).

Тогда F(х^*) = 1 - F(- х^*) = 0,5 - Ф(- х^*) = 0,02. Отсюда Ф(- х^*) = 0,5 - 0,02 = 0,48. По таблице находим х^* = - 2,05.

Необходимо снова перейти к N(600, 1600) и найти х^*`, для которого х<sup>*</sup> = (х<sup>*</sup>` - 600)/40. Отсюда х^*` = 40*х^* + 600 = 600 - 82 = 518.

Следовательно, 2% ламп работают не более 518 часов.

Если бы было необходимо определить срок работы 2% лучших ламп, то нужно было бы найти х^*, для которого F(х^*) = 1 - 0,02 = 0,98 = 0,5 + Ф(х^*), т.е. Ф(х^*) = 0,48. По таблице х^* = 2,05; х^*` = 40*х^* + 600 = 600 + 82 = 682.

Следовательно, 2% ламп работают не менее 682 часов.