 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Плотность и функция распределения. Непрерывные случайные величины
|
|
Выше были рассмотрены законы распределения дискретных случайных величин.
Каким образом можно представить закон распределения непрерывной случайной величины, т.е. величины, которая может принимать любые значения на некотором промежутке числовой оси, и число ее возможных значений всегда бесконечно?
Для непрерывной случайной величины вероятность того, что она примет какое-то одно определенное значение, всегда равна нулю. Но можно определить вероятность того, что эта величина примет значение из некоторого промежутка.
Для этого можно использовать функцию плотности распределения вероятности f(x) (ее еще называют плотностью вероятности или плотностью распределения).
Вероятность того, что непрерывная случайная величина х примет значение из некоторого промежутка [a;b], определяют по формуле:
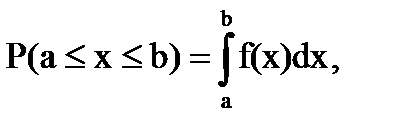
где подынтегральную функцию f(x) называют плотностью распределения.
Из формулы для 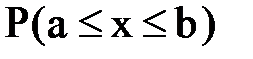 видно, что эта вероятность представляет собой не что иное, как площадь под кривой графика плотности вероятности f(x) на промежутке [a;b]. Это следует из геометрического смысла определенного интеграла.
видно, что эта вероятность представляет собой не что иное, как площадь под кривой графика плотности вероятности f(x) на промежутке [a;b]. Это следует из геометрического смысла определенного интеграла.
Если случайная величина х может принимать значения на всей числовой оси, то ее плотность распределения f(x) должна удовлетворять условиям:
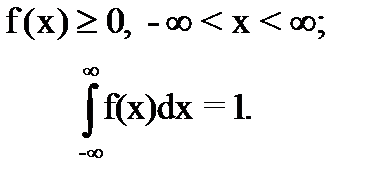
Если х распределена не на всей числовой оси, а на некотором ее промежутке, соответственно берутся границы этого промежутка.
Первое из условий для плотности вероятности означает, что вероятность не может быть отрицательной, а второе – что сумма вероятностей на всем пространстве событий должна быть равна 1.
Отметим, что для дискретной случайной величины функцию Р(х), определяющую закон ее распределения (вероятность, что она примет заданное значение), тоже называют плотностью вероятности: 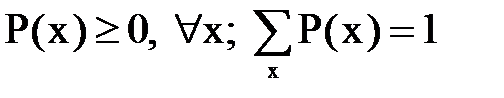 .
.
Кроме того, закон распределения случайной величины может быть задан функцией распределения вероятности (или просто функцией распределения) F(а). Эта функция определена на множестве действительных чисел и представляет собой вероятность того, что случайная величина примет значение х, меньшее а: F(а) = P(х < а).
Для дискретной случайной величины 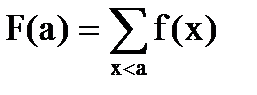 , причем эта функция будет ступенчатой, так как плотность вероятности определена только для дискретных значений (а функция распределения определена на всей числовой оси для любых случайных величин). Поэтому строгое определение непрерывной случайной величины вводится через понятие функции распределения: случайную величину называют непрерывной, если непрерывна ее функция распределения.
, причем эта функция будет ступенчатой, так как плотность вероятности определена только для дискретных значений (а функция распределения определена на всей числовой оси для любых случайных величин). Поэтому строгое определение непрерывной случайной величины вводится через понятие функции распределения: случайную величину называют непрерывной, если непрерывна ее функция распределения.
Представим графически функцию распределения дискретной случайной величины для рассмотренного ранее примера, в котором игрок мог выиграть или проиграть определенную сумму с заданными вероятностями. Плотность вероятности выигрыша х была задана таблично (во второй строке таблицы 1). Припишем к таблице 1 значения функции распределения для дискретных значений х (табл.3), а кроме того, поменяем столбцы местами, чтобы расположить значения случайной величины по возрастанию (для удобства построения графика).
Вероятность того, что выигрыш составит меньше, чем (-300), нулевая. Поэтому для а ≤ -300 F(a) = 0*. Меньше выиграть (больше проиграть) просто нельзя.
Вероятность того, что выигрыш будет менее 500, равна 0,7, т.е. F(500) =
= 0,7. В самом деле, такой выигрыш можно получить, только проиграв 300 с вероятностью 0,7. Вероятность выиграть менее 499, 400, 350 и т.д. от -300 до 500 (включая 500) также равна 0,7 по той же причине. Поэтому для
-300 < а ≤ 500 F(a) = 0,7.
Вероятность выиграть менее 1000 равна 0,9, так такой выигрыш означает, что выиграно либо -300, либо 500, и по аксиоме сложения 0,2 + 0,7 = 0,9. Следовательно, F(1000) = 0,9. По той же причине F(501) = F(510,5) =
= F(800) = … = 0,9, т.е. для 500 < а ≤ 1000 F(a) = 0,9.
И, наконец, для любого выигрыша свыше 1000 вероятность выиграть меньше этого значения случайной величины равна 1. Поэтому что это событие – достоверное. Все возможные значения выигрыша меньше 1000. Итак для
а > 1000 F(a) = 1.
Таблица 3
| х | -300 | ||
| Р(х) | 0,7 | 0,2 | 0,1 |
| F(x) | 0,7 | 0,2 + 0,7 = 0,9 |
Итак,
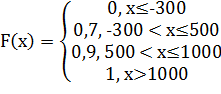
Построим график этой функции распределения, который будет иметь вид ступенчатой функции (рисунок 12).
| 0,9 |
| 0,7 |
| 0,2 |
| -300 |
| х |
| F(х) |
| Рис.1 |
| -300 |
| х |
| F(х) |
| 0,7 |
| 0,9 |
| Рисунок 12 – Функция распределения дискретной случайной величины |
Функция распределения F(x) обладает следующими свойствами:
1) 0 ≤ F(x) ≤ 1 (по свойствам вероятности);
2) 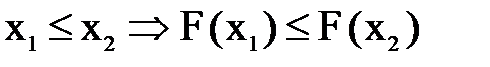 , т.е. F(x) монотонно не убывает на всей числовой оси (доказательство опустим);
, т.е. F(x) монотонно не убывает на всей числовой оси (доказательство опустим);
3) 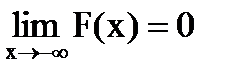 , как вероятность невозможного события;
, как вероятность невозможного события;
4)  , как вероятность достоверного события;
, как вероятность достоверного события;
5) вероятность 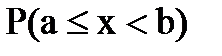 можно вычислить с помощью функции распределения, как приращение этой функции:
можно вычислить с помощью функции распределения, как приращение этой функции: 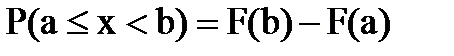 (доказательство опустим).
(доказательство опустим).
Таким образом, вероятность 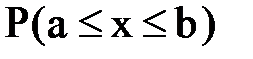 можно вычислить как с помощью функции распределения, так и с помощью плотности распределения:
можно вычислить как с помощью функции распределения, так и с помощью плотности распределения: 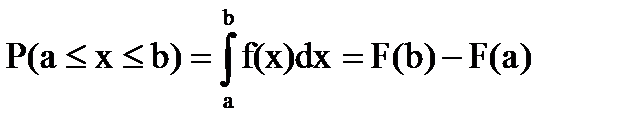 .
.
Между плотностью вероятности и функцией распределения непрерывной случайной величины существует следующая связь:
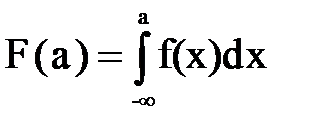 .
.
Иными словами, значение функции распределения будет представлять собой площадь под кривой графика плотности вероятности f(x) на промежутке ]-  ;а].
;а].
С другой стороны, плотность вероятности непрерывной случайной величины, является производной ее функции распределения: f(x) = F`(х).
Поэтому функцию распределения иногда называют интегральной функцией распределения, а плотность распределения – дифференциальной функцией распределения. График плотности распределения принято называть кривой распределения.
Для непрерывной случайной величины несколько иной вид примет формула математического ожидания (вместо суммы берется интеграл, который должен абсолютно сходиться, иначе математическое ожидание не существует): 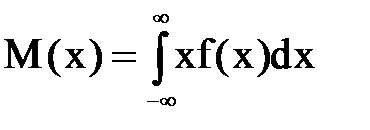 .
.
Дата публикования: 2015-10-09; Прочитано: 921 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
