Вероятность событий

Числовая функция Р, определенная на множестве событий, называется вероятностью, если

1) для любого события она неотрицательна (Р(А) 0, А),

2) для достоверного события равна единице (Р() = 1),

3) для попарно несовместных событий вероятность их суммы равна сумме вероятностей каждого события (если А_i*А_j = Æ (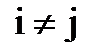), то ).

Последнее утверждение называют аксиомой сложения. Для двух событий она приет вид: А*В = Р(А + В) = Р(А) + Р(В).

Непосредственно из определения следует, что

1) Р(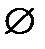) = 0 (так как );

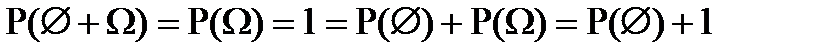2) Р(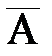) = 1 – Р(А) (так как );

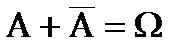3) 0 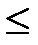Р(А) 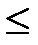1 (так как );

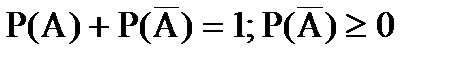4) 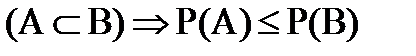, т.е. если А влечет за собой В, то вероятность А меньше, чем вероятность В (так как ).

Легко выводится правило сложения вероятностей. Представим события А + В = А + В 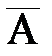и В = В 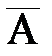+ ВА. События в правых частях равенств несовместны, поэтому их вероятности можно сложить по правилу для несовместных событий (аксиоме сложения):

Р(А + В) = Р(А) + Р(В );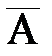

Р(В) = Р(В 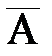) + Р(ВА).

Вычтем эти равенства почленно и перенесем Р(В) в правую часть:

Р(А + В) = Р(А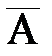) + Р(В )-Р(В 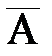)-Р(ВА) + Р(В);

Р(А + В) = Р(А) + Р(В)-Р(ВА).

Приведенное выше определение вероятности является аксиоматическим.

Если возможные исходы в пространстве элементарных событий равновероятны, используется классическое определение вероятности: вероятность любого элементарного события равна 1/n, где n – общее число элементарных событий. Вероятность случайного события А в соответствии с этим определением равна Р(А) = s/n, где s - число элементарных событий, входящих в соответствующее подмножество.

Это определение подходит, например, для опыта с бросанием монеты, в котором возможные исходы – “герб” или “решка” – равновероятны. Так как их 2, то вероятность каждого – ½. Четыре исхода опыта с двукратным бросанием монеты также равновероятны, и вероятность каждого из них – ¼.

А вот если рассматривать в качестве пространства элементарных событий число выпадений “решки” – 0, 1 или 2, то классическое определение вероятности применить нельзя, так как исходы не являются равновероятными. Тем не менее, вероятность любого из этих исходов можно подсчитать, если рассматривать их как случайные событий в пространстве элементарных событий {ГГ, РГ, ГР, РР}. Например, событие А – “решка выпала 1 раз” - включает в себя два элементарных события: Р(А) = Р{РГ, ГР} = 2/4 = 1/2.

Вероятность события В - “решка выпала хотя бы один раз” - также можно подсчитать с помощью классического определения – так как в него входит 3 элементарных события из четырех, Р(В) = ¾.

Те же результаты можно получить, если воспользоваться правилом сложения вероятностей (все элементарные события несовместны, и их вероятности равны ¼: ¼ + ¼ = ½; ¼ + ¼ + ¼ = ¾).

Вероятность события 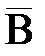, что “решка” не выпадет, равна ¼. Отметим, что Р(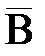) = 1-Р(В) = 1-¾.

На практике не всегда есть возможность судить о том, равновероятны элементарные исходы или нет. В самом деле, предположим, что нам неизвестен тот факт, что выпадение “герба” или “решки” равновероятно. В этом случае следует провести достаточно большое число опытов, например, 1000, и подсчитать число выпадений “решки” (или “герба”). Оно должно оказаться приблизительно равным 500, т.е. половине числа опытов, из чего и будет сделан вывод о равновероятности исходов. Отметим, что если при этом монета имеет какой-то дефект (например, одна ее сторона намагничена), из-за которого исходы действительно не будут равновероятными, в ходе испытаний это выяснится, и ложный вывод о возможности использования классического определения не будет сделан.

Другой пример эмпирического (опытного) определения вероятности – тестирование изделий на наличие брака. Взяв некоторое достаточно большое число изделий (например, 2000), проверим каждое из них. Пусть брак обнаружился в 346 изделиях. Из этого можно сделать вывод, что вероятность наличия брака равна 346/2000 = 0,173. Соответственно, вероятность отсутствия брака равна 1-0,173 = 0,827.

Итак, эмпирически вероятность можно определить, как относительную частоту появления определенного результата при достаточно продолжительном эксперименте, т.е. m/n, где n – достаточно большое общее число отдельных экспериментов, а m – число экспериментов, в которых имел место данный результат.

Иногда эмпирическое определение вероятности еще называют статистическим.

Кроме того, на практике часто встречаются случаи, когда нет ни теоретических данных, ни возможности провести эксперимент. В этом случае для определения вероятности используют экспертную оценку, т.е. ее субъективно оценивает опытный исследователь.

Например, прогноз менеджера по маркетингу: вероятность продажи 1000 единиц товара в первый месяц после его появления на рынке равна 0,4.

Другой пример оценки вероятности специалистом - метеопрогноз: Р(дождь) = 0,4; Р(ветер) = 0,7; Р(дождь и ветер) = Р(дождь*ветер) = 0,2. На этом же примере проиллюстрируем правило сложения вероятностей для событий, не являющихся несовместными. Подсчитаем вероятность того, что будет дождь или ветер: Р(дождь + ветер) = Р(дождь) + Р(ветер)-Р(дождь*ветер) = 0,4 + 0,7-0,2 = 0,9.

Если число исходов является бесконечным, имеет смысл использовать геометрическое определение вероятности. В соответствии с этим определением находят вероятность попадания точки в некоторую область. Геометрически вероятность события определяют как отношение меры области, которая соответствует тому, что событие произошло, к мере всей области.

Например, пусть покупатель может зайти в магазин в любой момент времени с 12.00 до 14.00. В 13.00 в магазине могут начать проводить дегустацию товара, которая будет продолжаться полчаса. Найдем вероятность того, что покупатель попадет на эту дегустацию. В качестве всей области рассмотрим отрезок числовой оси от нуля до двух (это те два часа, в течение которых может зайти покупатель). Его мера – длина – равна двум. Та область, которая соответствует дегустации, представляет собой часть этого отрезка длиной 0,5. Таким образом, искомая вероятность равна 0,5/2 = 0,25.

Рассмотрим более сложный пример. Пусть двое покупателей независимо друг от друга собираются прийти в магазин в произвольное время с 12.00 до 14.00. Каждый планирует пробыть там полчаса. Найдем вероятность того, что в магазине одновременно окажутся оба этих покупателя. Для этого обозначим х₁ – время прихода первого покупателя, а х₂ – второго. На рисунке 11 квадрат со стороной, равной двум, соответствует всей рассматриваемой области (его мера – площадь – равна 4). Покупатели окажутся в магазине одновременно, если между моментами их прихода пройдет не более получаса, т.е. |х₁ - х₂| ≤ 0,5. Это неравенство можно записать в виде х₁ - 0,5 ≤ х₂ ≤ х₁ + 0,5. На графике область пересечения этих полуплоскостей заштрихована.

Рисунок 11 – Геометрическое определение вероятности

Ее площадь можно вычислить по формуле 4 - 1,5*1,5 = 4 – 2,25 = 1,75. Тогда искомая вероятность равна 1,75/4 = 0,4375.