Требования к определению понятий

Чтобы оценить правильность явных определений, надо знать правила определения понятий. Так как преобладающее большин­ство определений в школьном курсе математики — это определе­ния через род и видовое отличие, то речь будет идти о правилах этих определений.

Прежде всего определяемое и определяющее понятия должны быть соразмерны. Это значит, что совокупности предметов, охва­тываемые ими, должны совпадать. Соразмерны, например, поня­тия «прямоугольник» и «четырехугольник, в котором вес углы прямые». Если же объем определяющего понятия включает в себя объем понятия определяемого, то говорят об ошибке слишком широкого определения. Так, определение «Прямые а и называют­ся параллельными, если они не имеют общих точек или совпада­ют» слишком широко, поскольку ему удовлетворяют и скрещива­ющиеся прямые. Если же объем определяющего понятия уже объема определяемого понятия, то имеет место ошибка слишком узкого определения. Например, определение «Прямые а и b называются параллельными, если они не имеют общих точек» слишком узко, поскольку ему не удовлетворяют совпадающие прямые.

Второе правило определения запрещает порочный круг: нельзя определять понятие через само себя или определять его через другое понятие, которое, в свою очередь, определяется через него. Возьмем такие понятия начальной математики, как «умножение» d «произведение», и дадим им следующие определения:

Умножением чисел называется действие, при помощи которого находят произведение этих чисел.

Произведением чисел называется результат их умножения.

Видим, что умножение определяется через понятие произ­ведения, а произведение — через понятие умножения. Определе­ния образовали, как говорят в математике, порочный круг, В pe­-

зультате цепочка последовательных определений, выстроенных в рамках курса, прерывается.

Порочный круг содержится и в таком определении: «Решением уравнения называется чисто, которое является его решением». Здесь понятие «решение уравнения» определяется, по сути дела, через решение уравнения.

Третьим важным требованием к логически правильному опре­делению понятия является следующее: в определении должны быть указаны все свойства, позволяющие однозначно выделять объекты, принадлежащие объему определяемого понятия.

Рассмотрим, например, такое определение понятия «смежные углы»: «Смежными называются углы, которые в сумме составляют 180°». Нетрудно увидеть, что под данное определение можно подвести не только углы, изображенные на рисунке 2 и действи­тельно являющиеся смежными, но и углы, изображенные па ри­сунке 3. Почему так произошло? Дело в том, что в приведенном определении смежных углов указано лишь одно их свойство, а именно свойство составлять в сумме 180°, но его недостаточно для выделения смежных углов из всех других.

Еще одно требование к правильному определению понятия — отсутствие в нем избыточности. Это означает, что в определении не должно быть указано лишних свойств, вытекающих из дру­гих свойств, также включенных в определение понятия.

Рассмотрим определение: «Прямоугольником называется че­тырехугольник, у которого противоположные стороны равны и все углы прямые». Можно показать, что включенное в определение свойство «иметь противоположные равные стороны» вытекает из свойства «иметь прямые углы». Следовательно, данное определе­ние прямоугольника избыточное и правильнее определять прямо­угольник таким образом: «Прямоугольником называется четырех­угольник, у которого все углы прямые».

Следует сказать, что в любом определении понятия есть эле­мент произвола, что проявляется, во-первых, в выборе термина (прямоугольник, в котором все стороны равны, мог бы называться и по-другому), а во-вторых, в выборе свойств, включаемых в оп­ределение. В принципе понятие квадрата можно определить так: «Квадратом называется ромб, у которого все углы прямые» — или так: «Квадратом называется параллелограмм, у которого все стороны равны, а углы прямые». Различные определения одного и того же понятия возможны потому, что из большого числа свойств, входящих в содержание этого понятия, в определение включаются только некоторые.

Если одному и тому же понятию даются, например, два раз­ных определения, то они должны быть равносильными. Это озна­чает, что из свойств, включенных в одно определение, должны вытекать свойства, положенные в основу другого определения, и наоборот.

Чем же руководствуются, когда из возможных определений некоторого понятия выбирают одно? Исходят из того, какое опре­деление проще, естественнее или целесообразнее для дальнейшего построения теории.

Если же какие-либо свойства оказываются включенными в определение, то другие свойства тех же объектов могут быть логи­чески выведены из тех, что вошли в определение. Это важное по­ложение используют при решении задач на распознавание. Если объект А принадлежит объему определяемого понятия, то он обладает всеми свойствами, которые указаны в определении понятия. Справедливо и обратное утверждение, т. с. если известно, что объект А обладает всеми свойствами, которые указаны в определении понятия, называемого некоторым термином, то и объект А можно назвать этим термином.

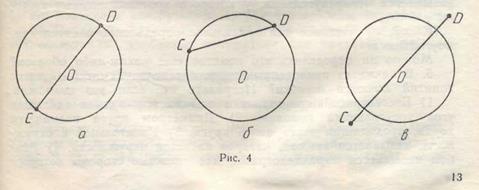
Пример. Используя определение диаметра окружности, установим, в каком из случаев, представленных на рисунке 4, отрезок CD является диаметром.

Определим диаметр окружности следующим образом: диамет­ром окружности называется хорда, проходящая через ее центр. Чтобы отрезок CD оказался диаметром окружности, достаточно одновременное выполнение двух условий: отрезок CD должен быть хордой окружности и проходить через ее центр. Этим двум условиям удовлетворяет отрезок CD в случае «а». В случае «б» отрезок CD — хорда, но он не проходит через центр окружности; в случае «в» отрезок CD проходит через центр окружности, но не является хордой.

Еще одним требованием к логически правильному определе­нию понятия является следующее: необходимо, чтобы определяе­мый объект существовал. Рассмотрим, например, такое определе­ние: «Тупоугольным треугольником называется треугольник, у которого все углы тупые». Нетрудно убедиться в том, что треуголь­ник, у которого все углы тупые, не существует. Следовательно, данному определению реально ничего не соответствует, и поэтому оно не может считаться логически правильным.

Заметим, что в математике для ответа на вопрос, существует ли объект, удовлетворяющий данному определению, как прави­ло, доказывают специальную теорему, подтверждающую возмож­ность существования объекта, о котором говорится в определении. В геометрии существование объекта, удовлетворяющего опреде­лению, иногда обосновывают построив его.