Теорема про додавання прискорень 1 страница

Теорема Коріоліса. Абсолютне прискорення точки в складному русі дорівнює геометричній сумі трьох прискорень: відносного, яке характеризує зміну відносної швидкості точки у відносному русі; переносного, яке характеризує зміну переносної швидкості точки в переносному русі, і прискорення Коріоліса, яке характеризує зміну відносної швидкості точки в переносному русі й переносної швидкості точки у відносному русі.

Доведення. Точка М здійснює складний рух (рис.3). Знайдемо співвідношення між абсолютним 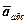, відносним 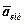і переносним 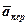прискореннями.

Для визначення 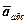будемо розглядати приріст вектора 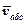на абсолютному елементарному переміщенні 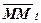(позначимо через d), для визначення 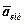– приріст вектора 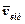на відносному елементарному переміщенні 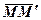(позначимо d₁), для визначення 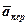– приріст вектора 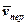на переносному елементарному переміщенні 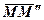(позначимо d₂), тобто:

.

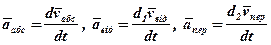Оскільки у складному русі

,

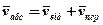то

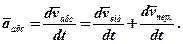
Беручи до уваги те, що абсолютне елементарне переміщення 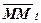дорівнює геометричній сумі відносного 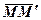і переносного 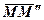елементарних переміщень, маємо:

,

де 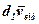– елементарний приріст вектора 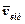на відносному переміщенні 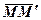, 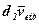– елементарний приріст 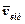на переносному переміщенні 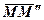. Для визначення 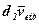враховуємо, що переносний рух складається в загальному випадку із поступального переміщення разом з деякою точкою О і повороту навколо цієї точки. Позначивши кутову швидкість через і використавши співвідношення 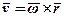, маємо:

.

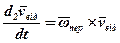Тоді знаходимо:

.

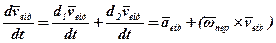Аналогічно запишемо:

,

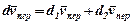де 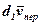– елементарний приріст вектора 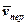на відносному переміщенні 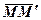, 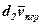– елементарний приріст 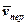на переносному переміщенні .

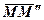Оскільки 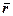має різні значення для точок М і М', тобто він змінюється у відносному русі, то скориставшись залежністю 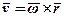, знайдемо:

,

де . Отже,

.

Тоді:

.

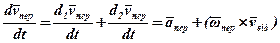Введемо позначення:

.

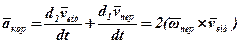Величина 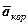називається поворотним або коріолісовим прискоренням точки і характеризує зміну вектора відносної швидкості 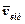у переносному русі й вектора переносної швидкості 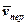у відносному русі.

Остаточно запишемо:

.

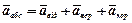Ця формула і виражає теорему Коріоліса. Для визначення прискорення Коріоліса використовують формулу:

,

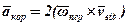тобто воно дорівнює подвоєному векторному добутку кутової швидкості переносного руху на відносну швидкість точки.

Якщо кут між векторами 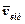і позначимо через α, то величина прискорення Коріоліса визначиться за формулою:

а_кор=2|ω_пер ν_від| sinα.

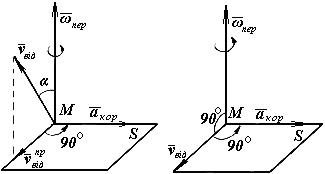
а) б)

Рис. 4

Вектор 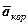напрямлений перпендикулярно площині, яка проходить через вектори і 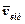у той бік, звідки найкоротше суміщення з 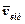проходить проти ходу годинникової стрілки (рис.4, а).

Якщо спроектувати вектор 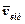на площину S, перпендикулярну , то повернувши проекцію 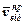на 90° у бік переносного обертання, також дістанемо напрямок прискорення Коріоліса (рис.4,а). Якщо відносний рух відбувається в одній площині, то кут α=90° (рис.4,б), і прискорення Коріоліса визначиться за формулою: а_кор=2|ω_пер·v_від|, а напрямок, повернувши вектор відносної швидкості 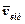на кут 90° у бік переносного обертання.

Із формули визначення прискорення Коріоліса виходить, що воно дорівнює нулю в таких випадках:

1) коли ω_пер.=0, тобто у випадку поступального переносного руху або в моменти, коли кутова швидкість непоступального переносного руху перетворюється на 0;

2) коли v_від = 0, тобто у випадку відносного спокою точки або в моменти, коли її відносна швидкість перетворюється на 0;

3) коли 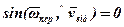, тобто у випадку, коли вектор відносної швидкості 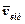точки в даний момент паралельний осі Оz переносного обертання.

Питання для самоконтролю

1.Який рух точки називається складним?

2.Дати означення відносному, переносному та абсолютному рухам. Навести приклад.

3.Сформулювати та довести теорему про додавання швидкостей у складному русі.

4.Сформулювати та довести теорему Коріоліса.

5.Що характеризує прискорення Коріоліса? Як воно визначається за величиною та напрямком?

6.В яких випадках прискорення Коріоліса дорівнює нулю?

Лекція № 15

Тема: “Складний рух твердого тіла”

План

1.Додавання поступальних рухів.

2.Додавання обертальних рухів навколо двох паралельних осей.

3.Додавання обертальних рухів навколо осей, які перетинаються.

1. Додавання поступальних рухів

Як було зазначено вище, складним називається такий рух твердого тіла, коли воно рухається відносно рухомих осей Oxyz (рис.1), а останні здійснюють деякий рух відносно нерухомих осей О₁х₁у₁z_1.

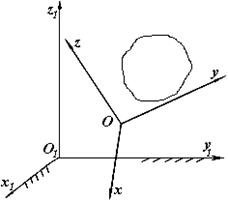Рис.1

Основними кінематичними характеристиками складного руху є його поступальні та кутові швидкості та прискорення. Ми зупинимось на визначенні тільки поступальних та кутових швидкостей.

Якщо відносний рух твердого тіла є поступальним зі швидкістю 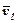, а переносний рух також поступальний зі швидкістю 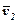, то очевидно, згідно теореми про додавання швидкостей будемо мати: 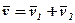, тобто абсолют-ний рух твердого тіла також буде поступальним.

Отже, при додаванні поступальних рухів із швидкостями 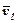і 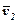результуючий рух тіла також буде поступальним зі швидкістю:

.

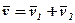2. Додавання обертальних рухів навколо двох паралельних осей

Нехай диск 1 обертається навколо осі О₁а, закріпленої на кривошипі 2, який у свою чергу обертається навколо осі О₂в (рис.2).

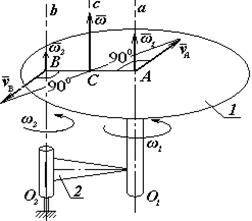Рис. 2

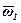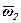Розглянемо спочатку випадок, коли диск 1 і кривошип 2 обертаються в один бік із швидкостями відповідно ω₁ і ω₂. Зобразимо кутові швидкості у вигляді векторів і ,напрямлених вздовж осей О₁а і О₂в. Як бачимо, диск бере участь одночасно в двох обертаннях: навколо осі О₁а з кутовою швидкістю ω₁ (відносний рух) і разом з кривошипом 2 навколо осі О₂в з кутовою швидкістю ω₂ (перенос-ний рух).

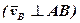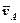Точка В дістає швидкість тільки від обертання відносно осі О₁а, а отже, ν_В=ω₁АВ . Аналогічно ν_А=ω₂АВ . Швидкості і 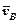точок А і В паралельні одна одній і напрямлені в протилежні боки. Миттьовий центр швидкостей у даному випадку буде в точці С, через яку проходить миттьова вісь Сс обертання диска.

Тоді:

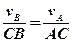або .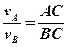

Підставивши значення швидкостей ν_В і ν_А,перепишемо співвідношення:

.

Результуючим рухом є обертання навколо миттьової осі Сс. Визначимо модуль миттьової кутової швидкості ω.

Швидкість точки В за модулем, з одного боку:

ν_В=ω₁АВ,

а з іншого боку

ν_В=ωВС.

Звідси:

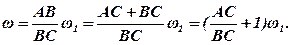
Підставивши замість відношення його значення, дістанемо остаточно:

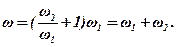
Отже, при додаванні двох напрямлених в один бік обертальних рухів навколо паралельних осей утворюється обертання навколо миттьової осі з абсолютною кутовою швидкістю, яка дорівнює сумі кутових швидкостей першого і другого обертань.

Положення миттьової осі Сс визначається із рівності:

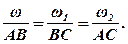
Рис.3

Якщо диск і кривошип обертаються в різні боки (рис.3), то швидкост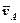і і 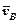напрямлені в один бік. Миттьовий центр швидкостей лежить на продовженні відрізка АВ. Тоді для модуля швидкості точки В маємо:

ν_В=ω₁АВ=ω ВС.

Звідси:

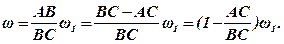
Підставивши замість останнього відношення його значення (див. вище), дістанемо остаточно:

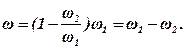
Отже, при додаванні двох напрямлених у протилежні боки обертальних рухів навколо паралельних осей також утворюється обертання навколо миттьової осі, але з абсолютною швидкістю, яка дорівнює різниці кутових швидкостей першого і другого обертань.

Якщо 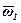= – 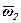, тобто диск і кривошип обертаються з однаковою кутовою швидкістю, але в протилежні боки, то в такому випадку говорять про пару обертань. Миттьовий центр швидкостей знаходиться в нескінченності, й усі точки диска в даний момент будуть мати однакові швидкості. Отже, коли 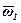= – 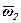, рух диска буде поступальним.

3. Додавання обертальних рухів навколо осей, які перетинаються

Нехай тіло обертається навколо осі О₁а, закріпленої на кривошипі 2, який обертається навколо осі О₂в. Причому осі перетинаються в деякій точці С (р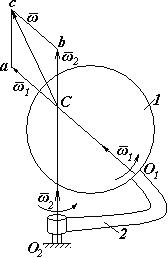ис.4).

Рис.4

Отже, тіло 1 бере участь одночасно в двох обертаннях: навколо осі О₁а з кутовою швидкістю 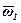(відносний рух) і разом з кривошипом 2 навколо осі О₂в з кутовою швидкістю 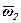(переносний рух). Якщо вектори 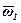і 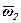перенесемо в точку С перетину осей і знайдемо їх геометричну суму, то визначимо абсолютну швидкість тіла:

.

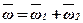Вектор напрямлений вздовж прямої Сс, яка проходить через точку С перетину осей обертання, і є не що інше, як миттьова вісь обертання тіла.

Отже, при додаванні двох обертальних рухів навколо осей, що перетинаються, абсолютна кутова швидкість тіла дорівнює геометричній сумі кутових швидкостей у відносному і переносному рухах.

Задача. Зубчатий механізм (рис.5) складається з двох зубчатих коліс 1 і 2 радіусами відповідно r₁ і r₂ та водила ОО₁, яке обертається з кутовою швидкістю ω. Колесо 1 нерухоме, а колесо 2 вільно насаджене на палець О₁ водила. Необхідно визначити абсолютну кутову швидкість 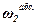і кутову швидкість відносно водила 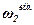колеса 2.

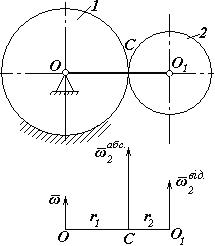Рис.5

Розв'язання. Оскільки точка С колеса 2 є точкою зчеплення з нерухомим колесом 1, вона в даний момент часу нерухома. Отже, точка С – миттьовий центр швидкостей колеса 2.

Обертання водила будемо розглядати як переносний рух для колеса 2. Побудуємо перпендикулярно ОО₁ вектори , 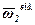і 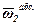переносної, відносної і абсолютної кутових швидкостей зубчатого колеса 2 (див. рис.5).

Скориставшись співвідношеннями, маємо:

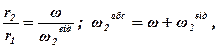
звідки:

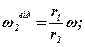
ω.

Питання для самоконтролю

1.Як додаються два поступальні рухи?

2.Як додати два обертальні рухи, напрямлені в один бік? Довести.

3.Як додати два обертальні рухи, напрямлені в різні боки? Довести.

4.Чому дорівнює абсолютна кутова швидкість тіла при додаванні двох обертальних рухів навколо осей, що перетинаються?

КІНЕМАТИКА МЕХАНІЗМІВ ТА МАШИН

Лекція № 16

Тема: “Структура та класифікація механізмів. Основні поняття та визначення”

План

1. Основні поняття та визначення механізму.

2. Класифікація кінематичних пар.

3. Умовне зображення ланок та кінематичних пар.

4. Кінематичний ланцюг, різновидності кінематичних ланцюгів.

1. Основні поняття та визначення механізму

Будь-який механізм складається з окремих деталей (тіл). У механізмах стаціонарного типу одні деталі нерухомі, інші рухаються якимось чином відносно них.

Кожна рухома деталь або група деталей, що утворюють одну жорстку рухому систему тіл, носить назву рухомої ланки механізму.

Всі нерухомі деталі утворюють одну жорстку нерухому систему тіл, яка називається нерухомою ланкою або стояком.

Таким чином, у будь-якому механізмі є одна або декілька рухомих ланок і лише одна нерухома.

З’єднання двох ланок, що дотикаються, яке допускає їх відносний рух, називається кінематичною парою.

Поверхні, лінії або точки ланки, по яких вона може дотикатись до інших ланок, утворюючи при цьому кінематичну пару, називаються елементами ланки.

Зв’язана система ланок, що утворюють між собою кінематичні пари, називається кінематичним ланцюгом.

Обмеження, накладені на відносний рух кожної ланки, називаються умовами в’язі в кінематичних парах.

Кожне тверде тіло, що вільно рухається в просторі має 6 ступенів вільності. Якщо забрати один рух, тобто накласти на тіло одну в’язь, то воно буде мати 5 ступенів вільності, наприклад, куля на площині (рис.1).

Очевидно, що кількість умов в’язі може бути тільки цілим числом і меншим шести (при S=6 ланки не можуть рухатись) і такою, що дорівнює або більше одиниці (оскільки при S<1 дві ланки не будуть дотикатися і будуть рухатися в просторі незалежно одна від одної), тобто:

1≤S≤5.

Отже, кількість ступенів вільності визначаються за формулою:

Н=6–S.

2. Класифікація кінематичних пар

Кінематичні пари класифікуються за трьома ознаками:

1) характером відносного руху ланок;

2) формою елементів ланок;

3) кількістю ступенів вільності.

1. За характером відносного руху ланок кінематичні пари поділяються на:

а) плоскі;

б) просторові.

Плоскими парами називають такі, в яких точки ланок, що утворюють кінематичну пару, описують траєкторії, які лежать в одній або паралельних площинах.

Просторовими парами називають такі, в яких точки ланок, що утворюють кінематичну пару, описують неплоскі траєкторії або траєкторії, які лежать у перетинних площинах.

2. За формою елементівланок кінематичні пари поділяються на:

а) вищі;

б) нижчі.

Вищою кінематичною парою називається така, дотикання ланок якої відбувається по лінії або в точці. Іншими словами, елементом якої є лінія або точка (наприклад, кулачкова та зубчата пари).

Нижчою кінематичною парою називається така, дотикання ланок якої відбувається по поверхні. До неї відносяться поступальна і обертальна пари.

Перевагою нижчих пар є їх відносно мале спрацювання, а недоліком – більша, ніж у вищих парах, втрата енергії на тертя в рівних умовах.

3. За кількістю ступенів вільності кінематичні пари поділяються на 5 класів у просторовому русі. Причому клас пари визначається кількістю умов в’язі, накладних на відносний рух ланок.

Розглянемо обертальну кінематичну пару (рис.2). Таке з’єднання ланок допускає один рух – обертання ланки 2 відносно ланки 1, а отже, накладено 5 умов в’язі. Тому ця кінематична пара п’ятого класу. Куля на площині – це кінематична пара першого класу (рис.1).

3.Умовне зображення ланок та кінематичних пар

Спочатку розглянемо, як умовно зображаються ланки механізмів на кінематичних схемах (таблиця 1).

Таблиця 1.