 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Закони тертя ковзання
|
|
Сила, яка перешкоджає ковзанню одного тіла по поверхні іншого в площині їх дотикання називається силою тертя ковзання.
Виникнення тертя між поверхнями обумовлене передусім шорсткістю поверхонь.
Сформулюємо основні закони тертя ковзання.
1.При спробі зрушити одного тіла по поверхні іншого в площині їх дотикання виникає сила тертя, яка набуває значень від 0 до Fгр, що називається граничною силою тертя.
Прикладена до тіла сила тертя напрямлена в бік, протилежний тому, куди сили, що діють на тіло, намагаються його зрушити.
2.Гранична сила тертя чисельно дорівнює добутку статичного коефіцієнта тертя на нормальний тиск (нормальну реакцію):
Fгр=ƒ0 N,
де ƒ0 – статичний коефіцієнт тертя – величина безрозмірна. Він визначається експериментально й залежить від матеріалу тіл, що дотикаються, а також від їх стану.
3.Значення граничної сили тертя не залежить від розмірів поверхонь, що дотикаються у процесі тертя.
Із перших двох законів виходить, що при рівновазі F ≤ Fгр або
F £ ƒ0 N.
Значення сили тертя в стані спокою визначається цією нерівністю, воно може бути будь-яким, але не більшим за Fгр Величині Fгр сила тертя дорівнює лише тоді, коли рушійна сила досягає такого значення, що при найменшому її збільшенні, тіло починає рухатись, ковзати по поверхні. Рівновагу, яка має місце, коли сила тертя дорівнює Fгр, називають граничною рівновагою.
Все, про що ми говорили вище, відноситься до тертя спокою.
При русі тіла сила тертя напрямлена в бік, протилежний руху, і дорівнює добутку динамічного коефіцієнта тертя на нормальний тиск:
F=ƒ N.
Динамічний коефіцієнт тертя ковзання ƒ також є величиною безрозмірною і визначається дослідним шляхом.
2. Реакції шорстких в’язей. Кут тертя
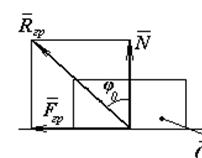 Реакція реальної (шорсткої) в’язі складається із двох складових: із нормальної реакції
Реакція реальної (шорсткої) в’язі складається із двох складових: із нормальної реакції 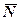 і перпендикулярної їй сили тертя
і перпендикулярної їй сили тертя 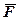 . Отже, повна реакція
. Отже, повна реакція  буде відхилена від нормалі на деякий кут. При зміні сили тертя від нуля до значення
буде відхилена від нормалі на деякий кут. При зміні сили тертя від нуля до значення 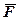 гр сила
гр сила  змінюється від
змінюється від 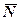 до
до  гр, а її кут з нормаллю зростає від нуля до деякого граничного значення φ0 (рис.1).
гр, а її кут з нормаллю зростає від нуля до деякого граничного значення φ0 (рис.1).
Найбільший кут φ0, який повна реакція шорсткої в’язі утворює з нормаллю до поверхні, називається кутом тертя.
Із креслення бачимо:
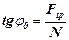 .
.
Оскільки Fгр=ƒ0·N, то звідси знаходимо такий зв’язок між кутом тертя і коефіцієнтом тертя:
tgφ0=ƒ0.
 При рівновазі повна реакція
При рівновазі повна реакція  може як завгодно проходити всередині кута тертя. Якщо рівновага стає граничною, то реакція буде відхилена від нормалі на кут φ0.
може як завгодно проходити всередині кута тертя. Якщо рівновага стає граничною, то реакція буде відхилена від нормалі на кут φ0.
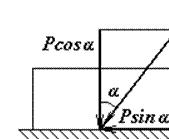
Якщо до тіла прикласти силу 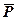 , що утворює кут α з нормаллю (рис.2), то тіло зрушиться тільки тоді, коли рушійна сила Psinα буде більшою Fгр=ƒ0·Pcosα (N=Pcosα, вагою тіла нехтуємо). А нерівність Psinα>ƒ0Pcosα, в якій ƒ0=tgφ0, виконується тільки при tgα>tgφ0, тобто α>φ0.
, що утворює кут α з нормаллю (рис.2), то тіло зрушиться тільки тоді, коли рушійна сила Psinα буде більшою Fгр=ƒ0·Pcosα (N=Pcosα, вагою тіла нехтуємо). А нерівність Psinα>ƒ0Pcosα, в якій ƒ0=tgφ0, виконується тільки при tgα>tgφ0, тобто α>φ0.
Отже, якщо сила утворює з нормаллю кут α, менший за кут φ0, то тіло уздовж даної поверхні зрушити не можна. Цим пояснюється явище самогальмування тіл.
3. Рівновага тіла при наявності тертя
Вивчення рівноваги тіл з урахуванням тертя ковзання можна звести до розгляду граничної рівноваги.
При аналітичному розв’язанні задачі реакцію шорсткої в’язі зображають двома її складовими 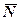 і
і 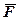 гр. Потім складають звичайні умови рівноваги, приєднуючи до них рівність Fгр=ƒ0 N. Із такої системи рівнянь і визначають шукані величини. Якщо необхідно визначити силу F, коли рівновага не є граничною (F≠Fгр), то F треба вважати невідомою величиною і визначати із відповідних рівнянь конкретно в кожній задачі.
гр. Потім складають звичайні умови рівноваги, приєднуючи до них рівність Fгр=ƒ0 N. Із такої системи рівнянь і визначають шукані величини. Якщо необхідно визначити силу F, коли рівновага не є граничною (F≠Fгр), то F треба вважати невідомою величиною і визначати із відповідних рівнянь конкретно в кожній задачі.
При геометричному способі розв’язання задачі реакцію шорсткої в’язі зручно зображати однією силою  , яка в граничному положенні відхилена від нормалі на кут φ0.
, яка в граничному положенні відхилена від нормалі на кут φ0.
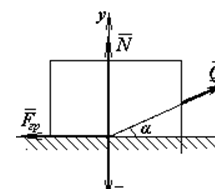 Задача. Вантаж вагою 20 Н лежить на горизонтальній площині (рис.3). Визначити, яку силу
Задача. Вантаж вагою 20 Н лежить на горизонтальній площині (рис.3). Визначити, яку силу 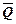 , напрямлену під кутом α= 300 до цієї площини, необхідно прикласти до вантажу, щоб зрушити його з місці. Статичний коефіцієнт тертя об площину ƒ0= 0,5.
, напрямлену під кутом α= 300 до цієї площини, необхідно прикласти до вантажу, щоб зрушити його з місці. Статичний коефіцієнт тертя об площину ƒ0= 0,5.
1.Розглянемо граничну рівновагу вантажу.
2.Зобразимо всі сили, що діють на вантаж: 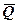 ,
, 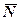 ,
, 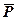 ,
, 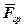 .
.
3.Складаємо умови рівноваги даної системи сил:
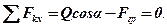
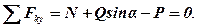
Із другого рівняння маємо:
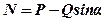 .
.
Тому:
Fгр=ƒ0N=ƒ0(P–Qsinα).
Підставимо це значення в перше рівняння, дістанемо:
Qcosα–ƒ0P+ƒ0Qsinα=0.
Звідси:
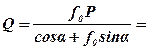
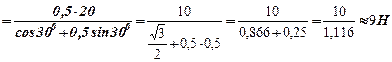 .
.
Питання для самоконтролю
1.Що називається силою тертя?
2.Сформулювати закони тертя ковзання.
3.Як визначається реакція шорсткої в’язі?
4.Дати поняття куту тертя.
5.Як визначається рівновага тіла при наявності тертя?
Лекція №9
Тема: “Просторова система сил”
План
1.Момент сили відносно осі. Обчислення головного вектора і головного моменту просторової системи сил.
2.Зведення просторової системи сил до найпростішого вигляду.
3.Рівновага довільної просторової системи сил. Випадок паралельних сил.
4.Розв’язання задач.
1.Момент сили відносно осі. Обчислення головного вектора і головного моменту просторової системи сил
На попередніх лекціях ми ввели поняття моменту сили відносно центра і сказали, що вектор 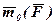 напрямлений перпендикулярно площині ОАВ (рис.1). Як це було і для сили, надалі нам необхідно буде розглядати проекції вектора
напрямлений перпендикулярно площині ОАВ (рис.1). Як це було і для сили, надалі нам необхідно буде розглядати проекції вектора 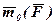 на різні координатні осі.
на різні координатні осі.
Проекція вектора 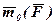 , тобто моменту сили
, тобто моменту сили 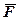 відносно центра О, на яку-небудь вісь z, що проходить через цей центр, називається моментом сили
відносно центра О, на яку-небудь вісь z, що проходить через цей центр, називається моментом сили 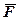 відносно осі z, тобто
відносно осі z, тобто
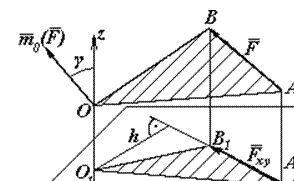
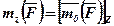 або
або 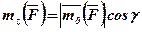 ,
,
де 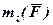 – момент сили
– момент сили 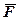 відносно осі z,
відносно осі z,
γ – кут між вектором 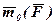 і віссю z.
і віссю z.
Із означення виходить, що 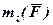 , як проекція вектора на вісь, величина алгебраїчна. Знак
, як проекція вектора на вісь, величина алгебраїчна. Знак 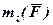 визначається так само, як і знак проекції будь-якого вектора, у нашому випадку
визначається так само, як і знак проекції будь-якого вектора, у нашому випадку 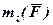 > 0.
> 0.
Знайдемо ще один вираз для визначення цієї величини. Для цього через довільну точку О1 осі z (див. рис.1) проведемо площину (xy ), перпендикулярну цій осі, й спроектуємо ∆ОАВ на цю площину. Оскільки вектор 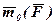 перпендикулярний площині ОАВ, а вісь z перпендикулярна Δ О1А1В1, то кут γ, як кут між нормалями до цих площин, буде кутом між цими площинами. Тоді:
перпендикулярний площині ОАВ, а вісь z перпендикулярна Δ О1А1В1, то кут γ, як кут між нормалями до цих площин, буде кутом між цими площинами. Тоді:
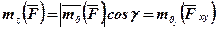 або
або 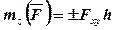 .
.
Отже, момент сили 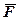 відносно осі z дорівнює алгебраїчному моменту проекції цієї сили на площину, перпендикулярну осі z, взятому відносно точки О1 перетину осі з цією площиною.
відносно осі z дорівнює алгебраїчному моменту проекції цієї сили на площину, перпендикулярну осі z, взятому відносно точки О1 перетину осі з цією площиною.
Це є друге означення моменту сили відносно осі.
Момент сили відносно осі буде мати знак плюс, коли з додатного кінця осі поворот, що прагне здійснити сила 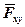 , бачиться проти ходу годинникової стрілки, а знак мінус – за ходом годинникової стрілки.
, бачиться проти ходу годинникової стрілки, а знак мінус – за ходом годинникової стрілки.
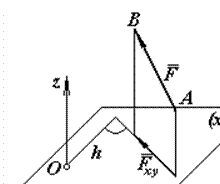 Послідовність обчислення моменту сили відносно осі (рис.2):
Послідовність обчислення моменту сили відносно осі (рис.2):
1) необхідно провести площину (xy ), перпендикулярну осі z;
2) спроектувати силу 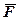 на цю площину і знайти величину Fxy;
на цю площину і знайти величину Fxy;
3). опустити із точки перетину О осі з площиною перпендикуляр на лінію дії 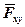 і знайти його довжину h;
і знайти його довжину h;
4) обчислити добуток Fxy·h;
5) визначити знак моменту.
Поодинокі випадки:
1) якщо сила паралельна осі, то її момент відносно осі дорівнює нулю (оскільки Fxy = 0);
2) якщо лінія дії сили перетинає вісь, то її момент відносно осі також дорівнює нулю (оскільки h=0);
3) якщо сила перпендикулярна осі, то її момент відносно цієї осі дорівнює взятому з відповідним знаком добутку модуля сили на відстань між лінією дії сили і віссю.
Поєднуючи пункти 1 і 2, відзначимо, що момент сили відносно осі дорівнює нулю, якщо сила і вісь лежать в одній площині.
Зазначимо, що теорема Варіньйона про момент рівнодійної справедлива і для моментів відносно будь-якої осі, тобто:
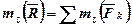 .
.
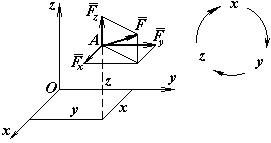
Рис.3
Аналітичні формули для моментів сили відносно координатних осей. Розкладемо силу 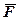 , прикладену в точці А з координатами x, y, z, на складові
, прикладену в точці А з координатами x, y, z, на складові 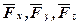 , паралельні координатним осям (рис.3).
, паралельні координатним осям (рис.3).
Оскільки 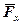 паралельна осі х, а
паралельна осі х, а 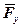 і
і 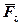 їй перпендикулярні, то з урахуванням знаків будемо мати:
їй перпендикулярні, то з урахуванням знаків будемо мати: 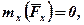
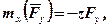
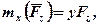 і в результаті
і в результаті 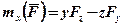 . Аналогічно знаходяться і моменти відносно осей y та z. Тоді остаточно маємо:
. Аналогічно знаходяться і моменти відносно осей y та z. Тоді остаточно маємо:
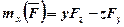 ;
;
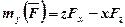 ;
;
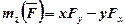 .
.
Ці формули дають аналітичні вирази для моментів сили відносно координатних осей.
Оскільки ліві частини наведених вище рівнянь є проекціями вектора 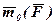 на координатні осі (де О початок координат), то:
на координатні осі (де О початок координат), то:
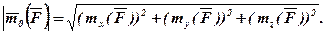
Обчислення головного вектора і головного моменту просторової системи сил. Як ми відзначили вище, значення головного вектора  і головного моменту
і головного моменту 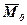 визначаються рівностями:
визначаються рівностями: 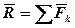 ;
; 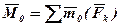 (див. лекц. №6).
(див. лекц. №6).
Покажемо, як  і
і 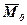 обчислюються аналітично, що нам надалі знадобиться. Вирази для Rx, Ry, Rz нам уже відомі (див. лекц. №3). Проекції вектора
обчислюються аналітично, що нам надалі знадобиться. Вирази для Rx, Ry, Rz нам уже відомі (див. лекц. №3). Проекції вектора 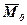 на координатні осі будемо позначати Mx, My та Mz. Тоді для визначення проекцій головного вектора
на координатні осі будемо позначати Mx, My та Mz. Тоді для визначення проекцій головного вектора  і головного моменту
і головного моменту 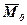 на осі координат маємо формули:
на осі координат маємо формули:
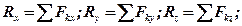
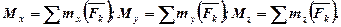
Отже, для задання (або визначення) будьякої системи сил, що діє на тверде тіло, достатньо задати (чи визначити) її головний вектор і головний момент відносно деякого центра, тобто шість величин, що входять у ліві частини рівнянь.
2. Зведення просторової системи сил до найпростішого вигляду
Ми вже говорили про те, що будь-яка система сил в загальному випадку зводиться до сили, що дорівнює головному вектору  , прикладеному в довільному центрі О, і до пари з моментом, що дорівнює головному моменту
, прикладеному в довільному центрі О, і до пари з моментом, що дорівнює головному моменту 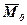 (лекц. №6).
(лекц. №6).
Визначимо, до якого найпростішого вигляду зводиться просторова система сил, яка не перебуває у рівновазі. Результат звичайно залежить від значень  і
і 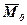 .
.
1. Якщо для системи 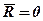 , a
, a 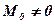 , то вона зводиться до пари сил з моментом, який дорівнює
, то вона зводиться до пари сил з моментом, який дорівнює 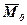 і обчислюється за формулами, наведеними вище.
і обчислюється за формулами, наведеними вище.
2. Якщо для системи 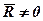 ,
, 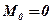 , то вона зводиться до рівнодійної, яка дорівнює
, то вона зводиться до рівнодійної, яка дорівнює  , лінія дії якої проходить через центр зведення О. Формули для обчислення
, лінія дії якої проходить через центр зведення О. Формули для обчислення  наведені вище.
наведені вище.
 3. Якщо для системи
3. Якщо для системи 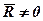 ,
, 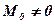 , але
, але 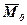
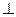
 , то система зводиться до рівнодійної, яка дорівнює
, то система зводиться до рівнодійної, яка дорівнює  , але не проходить через центр О.
, але не проходить через центр О.
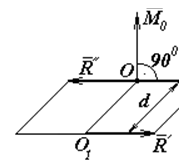
Дійсно, якщо 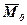
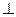
 , то пара, що зображає її вектор
, то пара, що зображає її вектор 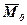 , і сила
, і сила  лежать в одній площині (рис.4). Тоді обравши
лежать в одній площині (рис.4). Тоді обравши 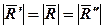 , дістанемо, що
, дістанемо, що  і
і 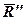 зрівноважать одна одну, і система заміниться тільки силою
зрівноважать одна одну, і система заміниться тільки силою 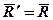 , лінія дії якої проходить через точку O1. Відстань OO1=d визначається за формулою
, лінія дії якої проходить через точку O1. Відстань OO1=d визначається за формулою 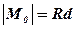 .
.
Цей випадок має місце, коли сили паралельні між собою або лежать в одній площині.
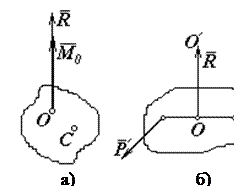 4. Якщо для системи сил
4. Якщо для системи сил 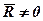 ,
, 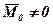 і при цьому вектор
і при цьому вектор 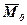 паралельний
паралельний  (рис.5,а), то це означає, що система сил зводиться до сукупності сили
(рис.5,а), то це означає, що система сил зводиться до сукупності сили  і пари
і пари 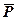 ,
, 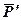 , що лежить у площині, перпендикулярній силі (рис.5,б).
, що лежить у площині, перпендикулярній силі (рис.5,б).
Така сукупність сили і пари називається динамічним гвинтом, а пряма ОО', уздовж якої напрямлений вектор  , віссю гвинта. До однієї сили або пари сил цю систему звести не можна.
, віссю гвинта. До однієї сили або пари сил цю систему звести не можна.
5. Якщо для системи 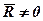 ,
, 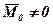 , і при цьому вектори
, і при цьому вектори  та
та 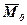 не перпендикулярні і не паралельні один одному, то така система теж зводиться до динамічного гвинта, але вісь його буде проходити через центр С (рис.5,а).
не перпендикулярні і не паралельні один одному, то така система теж зводиться до динамічного гвинта, але вісь його буде проходити через центр С (рис.5,а).
3. Рівновага довільної просторової системи сил. Випадок паралельних сил
Необхідні й достатні умови рівноваги будь-якої системи сил виражаються рівностями 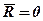 ,
, 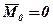 (див. лек. №6). Але вектори
(див. лек. №6). Але вектори  та
та 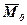 дорівнюють нулю тільки тоді, коли
дорівнюють нулю тільки тоді, коли 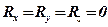 і
і 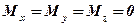 , тобто коли:
, тобто коли:
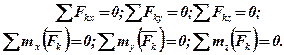
Таким чином, для рівноваги довільної просторової системи сил необхідно і достатньо, щоб суми проекцій всіх сил на кожну з трьох координатних осей і алгебраїчні суми їх моментів відносно цих осей дорівнювали нулю.
Якщо на тіло, крім сили, діє ще і пара сил, яка задається моментом 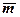 , то вигляд перших трьох рівнянь не зміниться (сума проекцій сил пар на будь-яку вісь дорівнює нулю), останні три матимуть вигляд:
, то вигляд перших трьох рівнянь не зміниться (сума проекцій сил пар на будь-яку вісь дорівнює нулю), останні три матимуть вигляд:
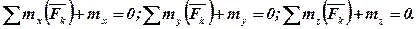
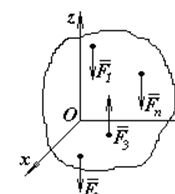 Випадок паралельних сил. Якщо всі сили, що діють на тіло, паралельні одна одній, можна обрати координатні осі таким чином, щоб вісь z була паралельна силам (рис.6). Тоді проекції кожної із сил на осі x та y і їх моменти відносно осі z будуть дорівнювати О, тому будемо мати тільки три умови:
Випадок паралельних сил. Якщо всі сили, що діють на тіло, паралельні одна одній, можна обрати координатні осі таким чином, щоб вісь z була паралельна силам (рис.6). Тоді проекції кожної із сил на осі x та y і їх моменти відносно осі z будуть дорівнювати О, тому будемо мати тільки три умови:
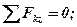
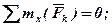
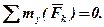
Отже, для рівноваги просторової системи паралельних сил необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил на вісь, паралельну силам, і алгебраїчні суми їх моментів відносно двох інших координатних осей дорівнювали нулю.
4.Розв’язання задач. Послідовність розв’язання задач статики просторової системи сил така сама, як і у випадку плоскої системи сил. З’ясувавши, рівновага якого тіла розглядається, необхідно зобразити всі зовнішні сили (і задані, і реакції в’язей) і скласти умови рівноваги. Із здобутих рівнянь визначаються шукані величини.
Для спрощення системи рівнянь рекомендується осі координат проводити так, щоб вони перетинали якомога більше невідомих сил або були їм перпендикулярні.
Якщо із загального креслення важко визначити, чому дорівнює момент якоїсь сили відносно осі, то слід зобразити на додатковому кресленні проекцію тіла разом із силою на площину, перпендикуляру цій осі.
Якщо виникають труднощі у визначенні проекції сили на відповідну площину або плеча цієї проекції, рекомендується розкласти силу на дві взаємо перпендикулярні складові (одна із яких паралельна якій-небудь координатній осі), а потім скористатись теоремою Варіньйона.
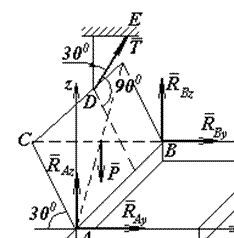 Задача. Прямокутна однорідна кришка вагою 120 Н утримується мотузкою DЕ (рис.7), перпендикулярною площині кришки. CD =
Задача. Прямокутна однорідна кришка вагою 120 Н утримується мотузкою DЕ (рис.7), перпендикулярною площині кришки. CD = 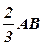 . Знайти реакції циліндричних шарнірів А та В і натяг мотузки.
. Знайти реакції циліндричних шарнірів А та В і натяг мотузки.
Будемо розглядати рівновагу кришки. На неї діють сили: 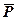 – вага,
– вага, 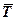 – реакція мотузки, реакція шарнірів –
– реакція мотузки, реакція шарнірів – 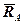 і
і 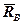 . Останні розкладемо на складові так, що
. Останні розкладемо на складові так, що 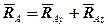 ,
, 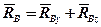 .
.
Усього маємо шість сил, із них п’ять невідомі. Всі сили перпендикулярні осі Ах, тому проекції їх на вісь Ах будуть дорівнювати нулю. Залишається п’ять рівнянь – саме стільки, скільки необхідно для розв’язання задачі.
Складемо рівняння рівноваги:
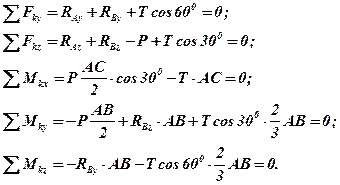
Із третього рівняння: 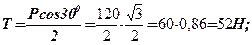
Із четвертого: 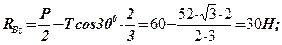
Із п’ятого: 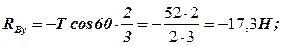
Із першого:
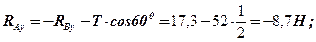
Із другого:
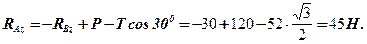
Питання для самоконтролю
1.Що називається моментом сили відносно осі?
2.В якій послідовності визначається момент сили відносно осі?
3.Назвати поодинокі випадки його визначення.
4.Довести аналітичні формули моментів сили відносно координатних осей.
5.Навести формули обчислення головного вектора і головного моменту просторової системи сил.
6.До якого найпростішого вигляду зводиться просторова система сил?
7.Які умови рівноваги довільної просторової системи?
8.Назвати умови рівноваги просторової системи паралельних сил.
МОДУЛЬ “КІНЕМАТИКА”
КІНЕМАТИКА МАТЕРІАЛЬНОЇ ТОЧКИ ТА ТВЕРДОГО ТІЛА
Лекція № 10
Тема: “Вступ. Способи задання руху точки. Вектори швидкості та прискорення”
План
1. Завдання кінематики, основні її поняття та визначення.
2. Кінематика точки. Способи задання руху точки.
3. Вектор швидкості точки.
4. Вектор прискорення точки.
1. Завдання кінематики, основні її поняття та визначення
Кінематикою називається розділ механіки, який вивчає рухи матеріальних тіл без урахування їх мас і сил, що діють на них.
Механічний рух відбувається у просторі та часі. Простір розглядається як трьохмірний. Час у класичній механіці вважається універсальним, тобто таким, що спливає однаково в різних системах відліку. Він є скалярною величиною, яка безперервно змінюється. У кінематиці час вважається незалежною змінною (аргументом). Решта змінних (відстань, швидкість, прискорення тощо) розглядаються як функції часу.
В основі кінематики лежать такі поняття як початковий момент часу, момент часу і проміжок часу. Початковий момент часу – це час, з якого починається відлік. Часто за початковий момент часу обирають значення t0=0. Даний момент часу визначається кількістю секунд, що проминули від початкового моменту. Проміжок часу – це різниця між будь-якими двома послідовними моментами часу.
Для визначити положення рухомого тіла відносно іншого вводиться поняття системи відліку. Система відліку – це система координат, яка жорстко зв'язана з тілом, по відношенню до якого вивчається рух. Оскільки в природі не існує нерухомих тіл, а отже, і абсолютно нерухомих систем відліку, то в механіці часто за умовно нерухому систему відліку обирають систему координатних осей, зв'язану з Землею.
Геометричне місце положень рухомої точки в обраній системі відліку називається траєкторією цієї точки. За виглядом траєкторії руху точки поділяються на прямолінійні та криволінійні.
У процесі вивчення руху точки слід розрізняти два важливих поняття: пройдений шлях і відстань. Відстань – це довжина відрізка траєкторії, відрахованого від деякої нерухомої точки, яка обирається за початок відліку. Відстань – величина алгебраїчна, оскільки в залежності від положення точки відносно початку відліку і від обраного напрямку осі вона може бути як додатною, так і від'ємною.
Рухаючись, точка за певний проміжок часу проходить деякий шлях, який вимірюється вздовж траєкторії в напрямку руху. Шлях може тільки збільшуватись, тому − це величина додатна. Шлях збігається з абсолютним значенням відстані тільки тоді, коли рух точки починається від початку відліку і відбувається по траєкторії в одному напрямі.
Для розв'язування задач кінематики необхідно, щоб рух був якось заданий (описаний). Задати рух або закон руху тіла (точки) – означає задати положення його відносно даної системи відліку в будь-який момент часу.
Кількість незалежних параметрів, які визначають положення точки, тіла або системи, називається кількістю ступенів вільності. Вільне тверде тіло має шість ступенів вільності в просторовому русі.
Головне завдання кінематики полягає в тому, щоб знаючи закон руху даного тіла або точки, визначити кінематичні характеристики (траєкторії, швидкості, прискорення) тіла в цілому і кожної його точки окремо.
Розпочнемо вивчення цього розділу із кінематики точки.
2. Кінематика точки. Способи задання руху точки
Задати рух точки можна одним із трьох способів: натуральним, координатним або векторним.
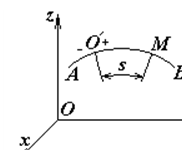 1. Натуральний спосіб. Цим способом користуються в тому випадку, коли траєкторія руху точки відома.
1. Натуральний спосіб. Цим способом користуються в тому випадку, коли траєкторія руху точки відома.
Нехай точка М рухається по деякій траєкторії АВ відносно обраної системи відліку (рис.1). Візьмемо на ній довільну точку 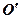 , яка буде за початок відліку. Траєкторію розглянемо як криволінійну координату. Домовимося про додатний і від'ємний напрямки руху.
, яка буде за початок відліку. Траєкторію розглянемо як криволінійну координату. Домовимося про додатний і від'ємний напрямки руху.
Тоді положення точки М буде визначатися криволінійною координатою s, яка дорівнює відстані від точки 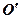 до точки М, що береться з відповідним знаком. У кожний момент часу точка може займати тільки одне відповідне положення на траєкторії, тому відстань s від початку відліку є деяка однозначна функція часу t. Залежність між змінними s і t називається законом руху точки М уздовж траєкторії.
до точки М, що береться з відповідним знаком. У кожний момент часу точка може займати тільки одне відповідне положення на траєкторії, тому відстань s від початку відліку є деяка однозначна функція часу t. Залежність між змінними s і t називається законом руху точки М уздовж траєкторії.
Спосіб задання руху точки у вигляді s=f(t) називається натуральним.
Отже, при натуральному способі задання руху точки повинні бути відомі:
- траєкторія точки в обраній системі відліку;
- початок відліку на траєкторії і додатний напрямок відліку;
- закон руху точки вздовж траєкторії: s=f(t).
 2. Координатний спосіб. Через те, що траєкторія руху точки відома далеко не завжди, на практиці частіше користуються координатним способом задання руху.
2. Координатний спосіб. Через те, що траєкторія руху точки відома далеко не завжди, на практиці частіше користуються координатним способом задання руху.
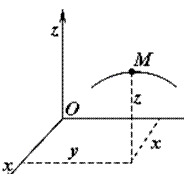
Положення точки по відношенню до даної системи відліку Оxyz можна визначити її декартовими координатами х, у, z (рис.2).
Під час руху точки М її координати будуть змінюватись з плином часу, тобто будуть деякими функціями аргументу t:
x = f1(t), y = f2(t), z = f3(t).
 Якщо ми будемо знати, як змінюються з часом координати точки, яка здійснює деякий рух, тобто будуть відомі ці рівняння, то ми завжди зможемо визначити положення її відносно обраної системи відліку.
Якщо ми будемо знати, як змінюються з часом координати точки, яка здійснює деякий рух, тобто будуть відомі ці рівняння, то ми завжди зможемо визначити положення її відносно обраної системи відліку.
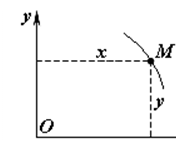
Якщо весь час точка рухається в одній площині, то, обравши останню за площину Оху, рух точки можна визначити двома рівняннями руху (рис.3):
х = f1(t), y = f2(t).
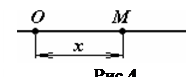 Якщо ж точка рухається прямолінійно, то траєкторію її руху (пряму) можна обрати за одну із координатних осей, наприклад, х. Рух точки в такому випадку буде описуватись одним рівнянням (рис.4):
Якщо ж точка рухається прямолінійно, то траєкторію її руху (пряму) можна обрати за одну із координатних осей, наприклад, х. Рух точки в такому випадку буде описуватись одним рівнянням (рис.4):
х =f(t).
Рівняння руху точки тут є одночасно і рівняннями її траєкторії.
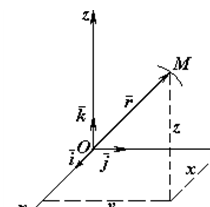 3. Векторний спосіб. Положення точки в будь-який момент часу можна визначити за допомогою вектора
3. Векторний спосіб. Положення точки в будь-який момент часу можна визначити за допомогою вектора 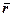 , проведеного із деякої точки О в дану точку М (рис.5).
, проведеного із деякої точки О в дану точку М (рис.5).
Вектор 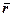 називається радіусом-вектором точки М. Оскільки з плином часу модуль і напрямок вектора
називається радіусом-вектором точки М. Оскільки з плином часу модуль і напрямок вектора 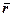 змінюються, то він є векторною функцією часу:
змінюються, то він є векторною функцією часу:
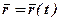 .
.
Це рівняння називається рівнянням руху точки у векторній формі. Воно виражає не тільки закон її руху, а й рівняння траєкторії точки у векторній формі.
Крива, яку описує кінець якого-небудь вектора за умови, що його початок знаходиться весь час в одній і тій же точці, називається годографом вектора. Отже, траєкторією точки М є годограф радіуса-вектора 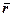 .
.
Зв'язок між векторним і координатним способами легко встановити, якщо ввести одиничні вектори (орти) осей 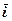 ,
, 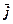 ,
, 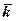 , тобто такі вектори, які чисельно дорівнюють одиниці й напрямлені вздовж осей x, y, z (рис.5). Обравши точку О за початок прямокутної системи координат і розклавши радіус-вектор по осях координат, маємо вираз для визначення положення точки М:
, тобто такі вектори, які чисельно дорівнюють одиниці й напрямлені вздовж осей x, y, z (рис.5). Обравши точку О за початок прямокутної системи координат і розклавши радіус-вектор по осях координат, маємо вираз для визначення положення точки М:
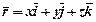 .
.
Векторний спосіб задання руху достатньо зручний для встановлення загальних закономірностей. Він дозволяє описати рух точки одним рівнянням на відміну від координатного, де кількість рівнянь дорівнює трьом. Але при розв'язуванні конкретних задач, коли вимагається чисельний результат, частіше зручнішими є координатний або натуральний способи.
3. Вектор швидкості точки
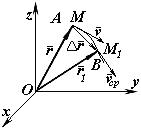 Рис.6
Рис.6
|
Однією з важливих кінематичних характеристик руху точки є її швидкість, яка є мірою руху точки і характеризує бистроту зміни її положення з плином часу. Швидкість – величина векторна.
Нехай деяка точка, яка здійснює рух по криволінійній траєкторії АВ, в момент часу t займає на траєкторії положення М, що визначається радіусом-вектором 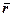 , а в момент t1 – положення М1, яке визначається радіусом-вектором
, а в момент t1 – положення М1, яке визначається радіусом-вектором 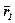 (рис. 6).
(рис. 6).
Тоді за проміжок часу 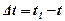 переміщення точки визначається вектором
переміщення точки визначається вектором 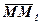 , який називається вектором переміщення точки. Із ΔОММ1 бачимо, що
, який називається вектором переміщення точки. Із ΔОММ1 бачимо, що
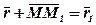 .
.
Звідси:
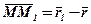 .
.
Відношення вектора переміщення точки до проміжку часу Δt назвемо середньою за модулем і напрямком швидкістю точки за цей проміжок часу Δt, тобто:
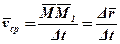 .
.
Середня швидкість 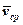 напрямлена вздовж хорди ММ1 у бік руху точки.
напрямлена вздовж хорди ММ1 у бік руху точки.
Очевидно, чим меншим буде проміжок часу Δt, тим точніше буде середня швидкість характеризувати рух точки. Якщо проміжок часу Δt прямує до нуля, то граничне значення швидкості наближається до значення швидкості в даний момент часу:
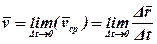 .
.
Таким чином, швидкістю точки в даний момент часу називається векторна величина 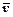 , до якої прямує швидкість
, до якої прямує швидкість 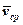 з наближенням проміжку часу до нуля. А оскільки граничне значення відношення
з наближенням проміжку часу до нуля. А оскільки граничне значення відношення 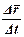 при Dt®0 є не що інше, як перша похідна від вектора
при Dt®0 є не що інше, як перша похідна від вектора 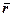 по аргументу t, то маємо:
по аргументу t, то маємо:
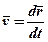 .
.
Отже, вектор швидкості в даний момент часу дорівнює першій похідній від радіуса-вектора точки за часом.
Оскільки граничним напрямком січної ММ1 є дотична, то вектор швидкості в даний момент часу напрямний по дотичній, яка проведена до траєкторії точки в бік її руху.
Якщо точка рухається прямолінійно, то вектор її швидкості 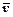 весь час напрямлений вздовж траєкторії точки (прямої), змінюється лише чисельно. Якщо траєкторія руху – крива, то вектор швидкості може змінюватись як за величиною, так і за напрямком. Рух, в якому швидкість з часом зростає, називається прискореним; рух, в якому швидкість з часом зменшується, називається сповільненим.
весь час напрямлений вздовж траєкторії точки (прямої), змінюється лише чисельно. Якщо траєкторія руху – крива, то вектор швидкості може змінюватись як за величиною, так і за напрямком. Рух, в якому швидкість з часом зростає, називається прискореним; рух, в якому швидкість з часом зменшується, називається сповільненим.
Дата публикования: 2015-09-18; Прочитано: 1688 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
