Определение характеристик моделируемого случайного процесса

Из первой теоремы нам известно, что спектральная плотность моделируемого процесса определяется как

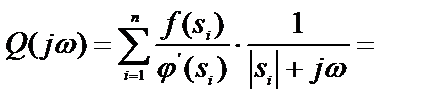
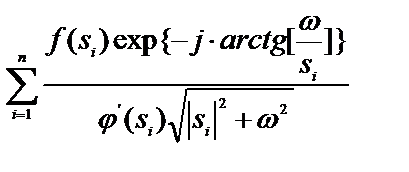. (39)

Следовательно, на основании теоремы Винера-Хинчина мы можем определить корреляционную функцию моделируемого процесса по формуле

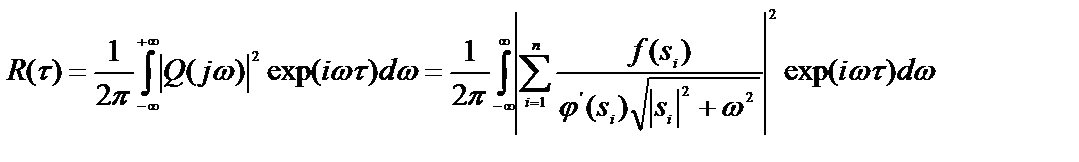. (40)

Для приближенного вычисления значений функции корреляции воспользуемся неравенством Буняковского – Шварца [4, 8]

.

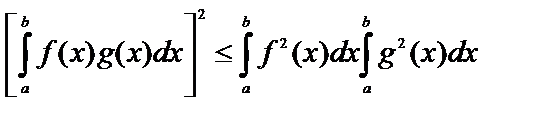Тогда

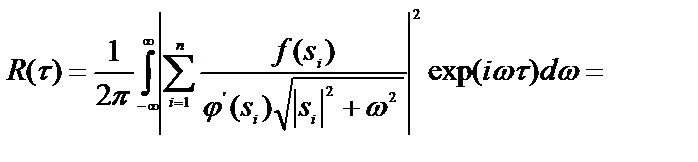(41)

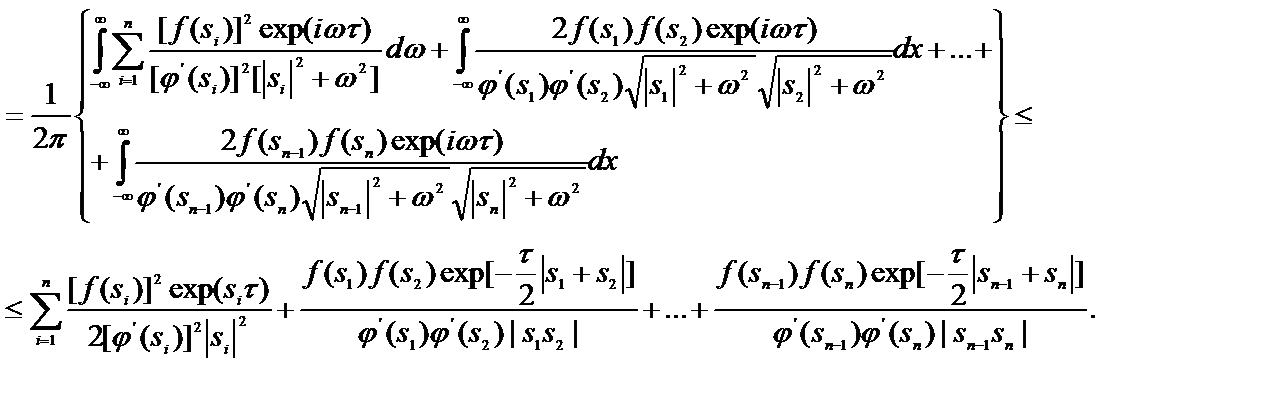
Интервал корреляции, определяемый как половина ширины основания прямоугольника единичной высоты, площадь которого равна площади под кривой модуля коэффициента корреляции, вычисляется по формуле [8]

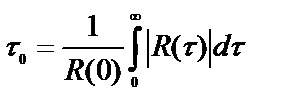(42)

Отметим, что более точные значения функции и интервала корреляции могут быть получены численными методами, [19].

Знание функции корреляции тем более полезно, что позволяет вычислить значение дисперсии показателя эффективности

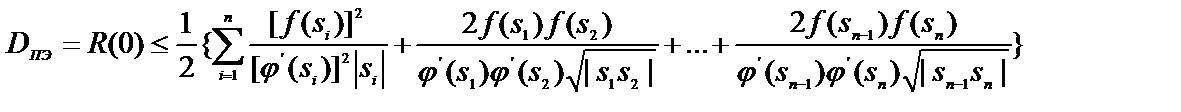(43)

и определить интервал времени

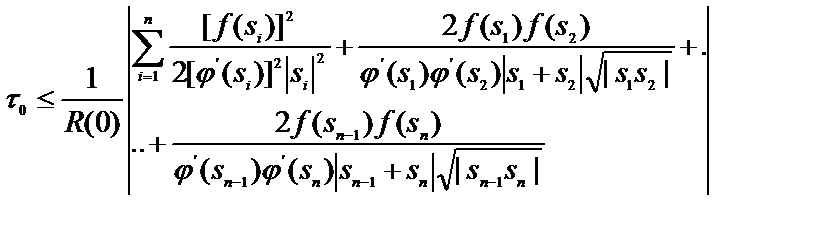, (44)

через который значения этого показателя могут считаться практически независимыми. В нашем случае, таким показателем является вероятность успешной передачи сообщений за время не более заданного.

Следовательно:

· математическое ожидание M[X(t)] процесса передачи сообщений по системе связи X(t) совпадает с вычисленными методами обращения или двухмоментной аппроксимации значениями P[t_П<T_З] вероятности успешной передачи сообщений за время t_П не более заданного T_З;

· дисперсией D[X(t)] моделируемого процесса X(t) является значение функции корреляции в нуле, вычисленное по ф(43);

· функция корреляции R(t) процесса передачи определяется в соответствии с ф(41);

· интервал корреляции t₀ рассчитывается по ф(44).

На основании теоремы 2 можно определить и одномерную плотность распределения моделируемого процесса

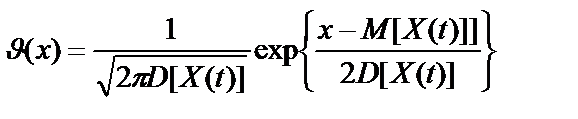, (45)

где x – наблюдаемые случайные значения частости (вероятности) успешной передачи сообщений за время не более заданного.

В том случае, когда наблюдаемым (контролируемым) параметром является время успешной передачи, математическое ожидание и дисперсия определяются по фф(27,28), а значения коэффициента и интервала корреляции остаются прежними. Это объясняется однозначной взаимозависимостью значений вероятности и времени успешной передачи сообщений, определяемых из функции распределения времени передачи.

Заметим, что если параметры эквивалентной функции изменяются в течение времени функционирования, что может иметь место при моделировании процессов передачи информации в условиях радиоэлектронного противодействия противника, стационарность исследуемого процесса может быть нарушена. Однако знание интервала корреляции позволит определять промежутки времени, в течение которых процесс можно считать стационарным.

С целью определения характеристик случайной величины интервалов времени, в течение которых процесс доведения сообщений X(t) соответствует предъявляемым требованиям, рассмотрим следующую постановку задачи.

Пусть в течение периода наблюдения статистические вероятности своевременной передачи сообщений в k -е моменты времени t _k принимали значения P _k и являются дискретными значениями реализации случайного процесса X(t), имеющего математическое ожидание M[X(t)] и дисперсию D[X(t)], вычисляемыми по ф.(27) и ф.(43) соответственно.

Определить среднюю длительность M[x] и дисперсию D[x] интервала времени x, в течение которого система связи будет соответствовать требованиям по вероятности передачи сообщений за время не более заданного.

Для решения этой задачи будем использовать методы теории выбросов. Предварительно заметим, что в силу теоремы 2 процесс X(t) является гауссовским.

В общем случае, вероятность того, что в момент времени ti -я реализация случайного процесса X_i(t) не пересечёт нижнего a(t) или верхнего y(t) барьеров равна:

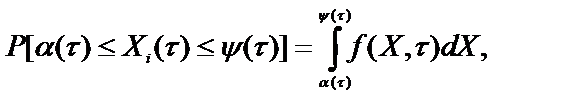(46)

а математическое ожидание длительности пребывания в области G{t, a(t)£X_i(t)£y(t), tÎx}

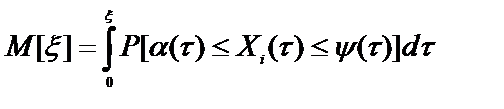, (46.а)

где x - оцениваемый интервал времени.

После подстановки (45) в (46) и (46.а) с учётом того, что задана только нижняя грань, то есть a(t)=P _з= const получим:

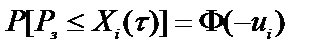(47)

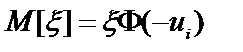(48)

где: u_i = [P_з– X_I(t)]/s_x, s_x = s_x(t) = const.

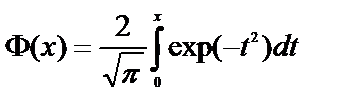- интеграл ошибок [18].

Для вычисления дисперсии D[x] необходимо задаться двухмерной плотностью распределения вероятностей для процесса X(t), то есть:

,

здесь: X_1i(t), X_2i(t) и s_x(t₁), s_x(t₂) - соответственно математическое ожидание и дисперсия значений обобщённого показателя качества функционирования в моменты времени t₁ и t₂; t₁ - t₂ = x; N - объём произведённой статистической выборки;

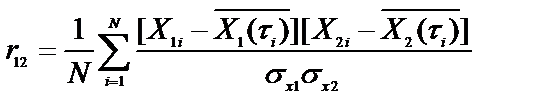- коэффициент корреляции;

Отсюда

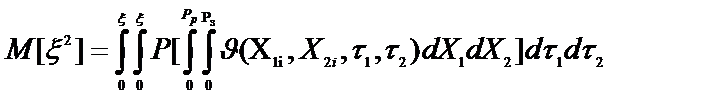, (49)

а 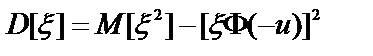. (50)

Определив численными методами [19] значение M[x²], в предположении, что r₁₂=0, x=t₁ - t₂; s_X1 = s_X2 = s_X = const и подставив полученный результат в (50) имеем

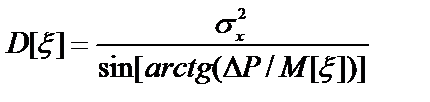, (51)

где DP = [X(t_i) – X(t_i-1)].

Результаты ф(47) – ф(51) целесообразно использовать при решении задачи прогнозирования состояния системы связи в следующий момент времени. При этом, глубина прогнозирования определяется длительностью интервала корреляции рассчитываемого по ф.(44).

В свою очередь, вероятность того, что значение показателя своевременности в любой момент времени будет не менее требуемого

,

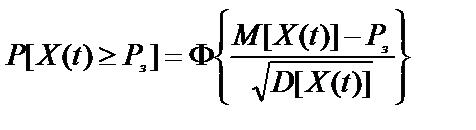а средняя длительность интервала времени, в течение которого система связи будет соответствовать требованиям

,

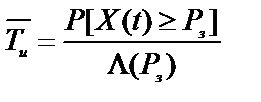где L(P_з) - математическое ожидание числа пересечений заданного уровня P_з.

Для определения математическое ожидание числа пересечений L(P_з) заданного уровня P_з. случайной функцией X(t) обозначим совместную плотность распределения вероятностей контролируемого параметра x и его производной

через f(x, x^’). Тогда математическое ожидание числа пересечений уровня P равно:

.

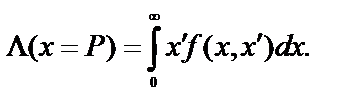В силу теоремы 2, процесс X(t) является гауссовым, а значит и его производная по времени тоже имеет нормальное распределение с нулевым математическим ожиданием, следовательно совместная плотность вероятностей

,

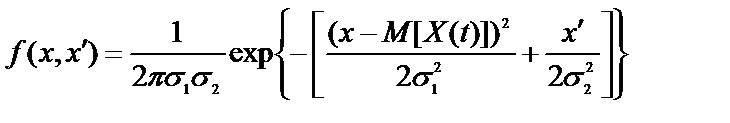где s₁, s₂ – средние квадратичные отклонения параметров x и x^’.

Отсюда

.

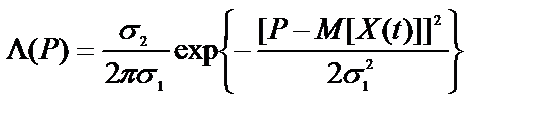С учетом того, что значения P выбираются, как правило, примерно равными M[X(t)] величина L(P) может быть определены непосредственно из корреляционной функции по формуле

,

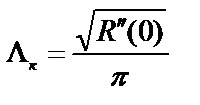при этом s₂ = 2ps₁L_к.

В том случае, когда задача решается в процессе боевого использования системы связи и имеется возможность статистического определения корреляционной функции для расчета L целесообразно использовать следующий подход.

Пусть R_i – значения функции корреляции в равноудаленных точках t_i. Тогда из условия дискретизации и с учетом периодичности реальных функций корреляции мы имеем разбиение D: t₁ = t₀ <t₁ <t₂ <…<t_N = t₂ на отрезке [t₁, t₂], [t₂ - t₁]=T; T – период функции корреляции.

Из непрерывности и дифференцируемости случайного процесса X(t) на каждом интервале [t_i, t_i-1] следует, что функция R(t) может быть с высокой точностью аппроксимирована многочленом степени n. То есть, функция корреляции R(t) может быть определена как сплайн S_n(t) степени n с узлами на сетке D:

.

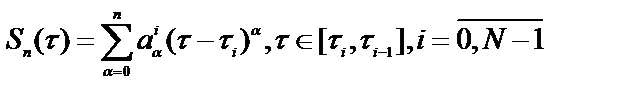Таким образом, задача определения R(t) сводится к линейной интерполяции рассчитанных экспериментальных величин сплайном S_n(t) с последующей аппроксимацией им реальной функции корреляции.

Исходя из требования дважды дифференцируемости R(t) можно считать достаточным использования в этих целях кубических сплайнов

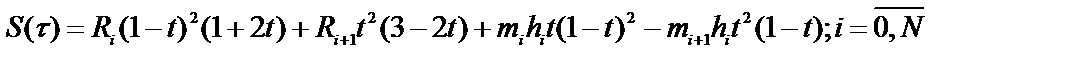, (56)

где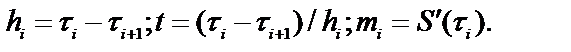

Отметим, что кубический сплайн S(t), представленный в виде (56) на каждом из промежутков [t_i, t_i-1] непрерывен вместе со своей первой производной всюду на отрезке [t₁, t₂]. Необходимые для построения сплайна S(t) значения m_i определяются из условия непрерывности второй производной S^’’(t)₊₀= S^’’(t)_-0 в точках t_i, i = 1,N и для периодических функций имеют вид:

.

.

.

;

.

.

.

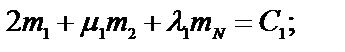
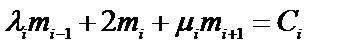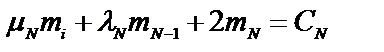
где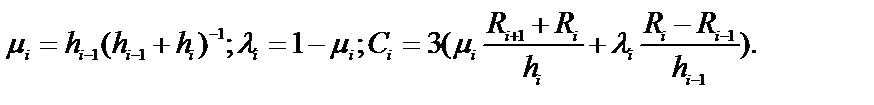

После вычисления значений m_i несложно определить вторую производную сплайна S(t) по формуле:

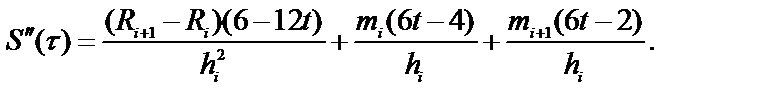(57)

Подставляя в (57) значения t=0, с учетом равенства (55) получим, что среднее число нулей процесса изменения показателя эффективности равно

.

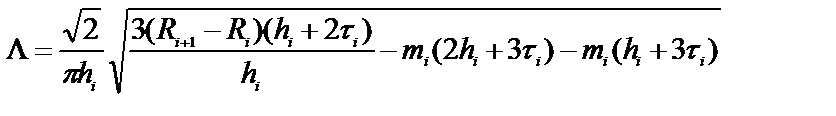Полученное значение L подставляется в ф(53).

В свою очередь, определение значений T_И позволяет на этапе планирования определить нормируемый в руководящих документах показатель устойчивости системы связи

,

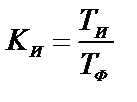а на этапе боевого использования по ф(47).