Виды стохастических сетей и их типовые структуры

Прежде чем приступить к рассмотрению видов стохастических сетей отметим один достаточно очевидный факт. Он состоит в том, что одному и тому же физическому процессу может соответствовать множество адекватных моделей, отличающихся друг от друга степенью детализации анализируемого процесса. Конкретный выбор модели и степень детализации определяется целями и задачами исследования, а также наличием на этапе постановки задачи исходных данных и их полнотой. То есть, входящие в состав стохастической сети элементы могут быть заведомо «не равноправными» и одни ветви могут представлять элементарные (неделимые) случайные процессы, в то время как другие представляют сложные, состоящие из многих элементарных, случайные процессы.

Именно этот факт и приводит к необходимости деления стохастических сетей на простые и сложные.

1. Простые стохастические сети.

Стохастическая сеть, состоящая из ветвей описывающих элементарные физические процессы и логических узлов (вершин) одного типа называется простой стохастической сетью.

Как следует из определения, данный вид сетей является достаточно широким. Однако на практике наибольшее применение нашли сети, содержащие логические вероятностные вершины «Исключающее ИЛИ». Это обусловлено тем, что в этом случае стохастическая сеть точно совпадает с определением алгоритма, в котором ветви соответствуют операторам действия, а промежуточные вершины условным операторам. Использование узлов других типов в простых стохастических сетях весьма ограниченно, так как моделирование реального случайного процесса при помощи только логического «И» или «Включающего ИЛИ» затруднительно и приводит, как правило, к сетям, содержащим одновременно несколько типов вершин и не соответствующим данному выше определению.

Очевидно, что целью моделирования процесса функционирования системы связи или ее элементов является получение аналитических выражений для вычисления значений показателей качества и эффективности. Это становится возможным только после определения эквивалентной функции, имеющей физический смысл вероятности реализации исследуемого процесса за время меньшее некоторого времени наступления катастрофы в системе. Под катастрофой понимается такое событие, что система перестает отвечать требованиям к качеству (эффективности) реализуемого ею целевого процесса. При этом поток наступления катастроф является пуассоновским (см. производящие и характеристические функции). Так как целевым процессом, при моделировании систем связи является процесс передачи (доставки) потоков сообщений, то катастрофой в этом случае является факт старения сообщений за время их передачи (доставки) по системе связи.

Понятно, что если сеть состоит из малого числа ветвей и в целом может быть преобразована к одной из базовых структур, то задача определения эквивалентной функции не вызывает никаких трудностей. Однако на практике приходится иметь дело с сетями, сведение которых к базовым достаточно сложно. Примером такой сети является простая стохастическая сеть, содержащая множество контуров (составных петель). Для изучения сетей данного типа введем понятия замкнутой стохастической сети и пели k -го порядка. Предварительно заметим, что петлей первого порядка принято называть петли, не содержащие других петель и позволяющие достичь каждый узел петли из любого другого.

Петлей k-го порядка называется множество k не связанных между собой петель первого порядка.

Эквивалентная функция петли k -го порядка определяется как

,

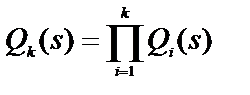где Q_i(s) – эквивалентная функция i -й петли первого порядка, определяемая как произведение эквивалентных функций ветвей, входящих в эту петлю.

Замкнутой стохастической сетью называется сеть, в которой каждая ветвь принадлежит, по крайней мере, одной петле.

Определение эквивалентной функции стохастической сети, по сути, преобразует исходную сеть в замкнутую. Это позволяет использовать для определения эквивалентной функции исходной сети топологическое уравнение Мейсона для замкнутых графов

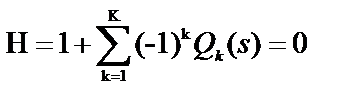(19)

здесь K – максимальный порядок петель, входящих в стохастическую сеть.

Анализ уравнения показывает, что в него входит и эквивалентная функция исходной стохастической сети, как замыкающая ветвь, образующая петлю первого порядка. Для пояснения рассмотрим сеть рис.6.

Рис. 6

Данная сеть содержит одну петлю первого порядка с эквивалентной функцией Q(s) = Q_a(s)Q_э(s). Из уравнения Мейсона: 1 - Q_a(s)Q_э(s) = 0 или Q_э(s)= Q_а^{- 1} (s). Важность этого результата состоит в том, что если в топологическом уравнении Q_a(s) заменить на Q_э^{- 1} (s) и решить его относительно Q_э(s), то будет получена искомая эквивалентная функция стохастической сети.

В качестве примера рассмотрим стохастическую сеть рис.7 [17].

Рис. 7

Чтобы определить эквивалентную функцию Q(s) данной стохастической сети необходимо:

1. Замкнуть стохастическую сеть фиктивной ветвью, исходящей из последнего (выходного) узла и входящей в первый (входящий) узел. На рис.7 эта ветвь показана пунктиром и характеризуется функцией Q_a(s).

2. Определить все петли k -го порядка:

петлипервогопорядка:

Q₁(s); Q₃(s)Q₄(s); Q₂(s)Q₃(s)Q₅(s); и Q₂(s)Q₃(s)Q₆(s)Q_a(s);

петля второго порядка:

Q₁(s)Q₃(s)Q₄(s).

3. С использованием топологического уравнения определить эквивалентную функцию сети.

Помня, что Q(s) = [Q_а(s)]^-1 из топологического уравнения получаем

H=1-Q₁(s)-Q₃(s)Q₄(s)-Q₂(s)Q₃(s)Q₅(s)-Q₂(s)Q₃(s)Q₆(s)Q^-1(s)+ Q₁(s)Q₃(s)Q₄(s)=0.

Отсюда

.

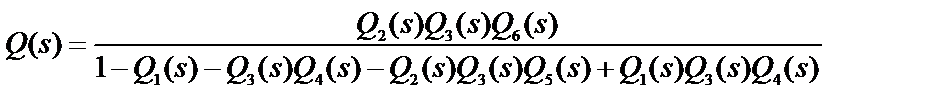Искомая эквивалентная функция найдена.

При определении эквивалентной функции мы полагали, что случайные времена реализации ветвей являются независимыми. В противном случае, необходимо обусловить преобразование Лапласа той ветви, для которой время ее реализации является зависимым, то есть [17]

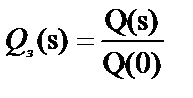
Таким образом, если имеется простая стохастическая сеть, состоящая из параллельных, последовательных цепей и петель, то при помощи топологического уравнения и использования базовых структур она может быть преобразована в эквивалентную сеть, содержащую единственную ветвь, характеризуемую эквивалентной функцией сети.