Алгоритмы синтеза графов с максимальной связностью при заданном числе вершин и ребер

Рассмотрены случаи построения графов, в том числе и с максимальной реберной связностью, когда заданы степенные последовательности вершин.

Однако чаще задача формализуется другим образом.

Задано: n – число вершин графа и m –число ребер, которые нужно распределить на вершинах графа таким образом, чтобы граф обладал наибольшей реберной связностью.

Харари показал, а Свами привел подробную процедуру построения графа H_k,n, который является k-связным и содержит ровно m=[kn/2] ребер. Процедура заключается в том, что в графе H_k,n между i-й и j-ой вершинами ребра прокладываются по следующим правилам:

I-случай k=2r-четно: тогда H_2r,n строится на вершинах v₀,v₁,…,v_n-1 и две вершины v_i и v_jсмежны, если i-r ≤ j ≤ i+r.

II-случай k =2r+1: n- четно: тогда H_2r+1,n получается из графа H_2r,n введением ребер, соединяющих вершины v_i и v_jдля i=0,1,2,…,n/2 и j=i+n/2(modn).

III-случай k=2r+1: n-нечетно, тогда H_2r+1,n получается из графа H_2r,n введением ребер, соединяющих вершины v_i и v_jдля i=0,1,2,…,(n-1)/2 и j=i+(n+1).2(mod n). Блок –схема алгоритма, реализующего процедуру Свами-Хараи приведена на рис.4.

Процедура работает при соблюдении равенства m=[k.n/2] с учетом выполнения требования 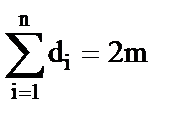. В этом ограничение процедуры.

При произвольном m и n и естественном ограничении 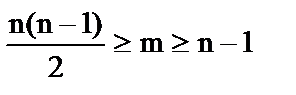хорошо работает алгоритм Колесникова-Федорова.

Суть его заключается в следующем. Для синтеза оптимальной структуры ее граф строят путем набора различных последовательных структур в виде независимых остовных деревьев или поддеревьев. При этом каждая новая последовательная структура для повышения равномерности распределения значений степеней вершин должна начинаться с другой вершины и порядок чередования вершин следует менять.

Элементы матрицы смежности, отображающие эти последовательные структуры, размещаются параллельно главной диагонали, состоят из одной или двух поддиагоналей и содержат n-1 или менее элементов.

Метод работает при любом соотношении m и n. Тонким моментом алгоритма является выбор вершины перехода на очередную диагональ, поскольку его иногда не удается формализовать, но реализовать эвристически просто из-за наглядности “ручной” реализации.

Оба алгоритма дают одинаковые результаты, когда k = 2m/n – целое число. Для исключения эвристических решений, когда k = 2m/n – не целое число, метод может быть усовершенствован и существенно упрощен путем переноса процесса оптимизации из области формирования последовательных структур в область формирования оптимальных (рациональных) степенных последовательностей вершин синтезируемого графа.

Рис.4. Блок-схема алгоритма, реализующего процедуру Свами-Харари.

При этом требование максимальной равномерности степеней вершин и равномерного распределения оставшихся ребер удовлетворяется следующим образом.

Определяется минимальная степень вершин d_imin=[2m/n] в остатке получается 1≤ r ≤ n-1 вершин, это значит, что n-r вершин имеют степень d_imin, а r- вершин имеют степень d_imах= d_imin+1. Причем порядок распределения вершин с разными степенями должен быть также максимально равномерным. При этом, если r<n/2, то распределяются d_imах, если r≥n/2, то распределяются d_imin.

Естественно, что количество оставшихся вершин должно быть четным (каждое ребро содержит 2 вершины), а получаемая последовательность - графической.

Далее по полученной степенной последовательности строится граф максимальной связности с использованием ℓ-процедуры [1 ].

Пример. Дано n=4, m=5 построить граф максимальной связности.

Решение

Определим k= d_imin = (2m /n)+r = 2.5/4 =2+2(mod4).

d_imax = d_imin +1=3

Определим степенную последовательность- это П₁= {2;3;2;3} или П₂ = {3;2;3;2}.

С помощью ℓ-процедуры строим граф по П₁:

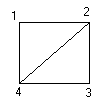
2 3 2 3 1. Соединяем 1 со 2^-ой и 4^-ой вершин

0 2 2 2 2. Соединяем 2^-ой со 3^-й и 4^-й вершин

0 0 1 1 3. Соединяем 3^-ю и 4^-ю вершин

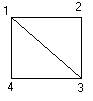Построим граф по П₂:

3 2 3 2 1. Соединяем 2^-ю с 1^-й и 3^-й вершин

2 0 2 2 2. Соединяем 1^-ой с 3^-й и 4^-й вершин

0 0 1 1 3. Соединяем 3^-ю и 4^-ю вершин

Графы изоморфны, граф G₂(П₂) получается из графа G₁(П₁) поворотом на 90 ^ο против часовой стрелки вокруг центра симметрии с помощью подстановки

1 2 3 4

t = 4 1 2 3

Как и следовало ожидать, оба графа имеют максимальное (при заданных m и n) число остовных деревьев- 8.